ESL3.2(下)最小二乘法学习笔记(含施密特正交化,QR分解)
这是一篇有关《统计学习基础》,原书名The Elements of Statistical Learning的学习笔记,该书学习难度较高,有很棒的学者将其翻译成中文并放在自己的个人网站上,翻译质量非常高,本博客中有关翻译的内容都是出自该学者的网页,个人解读部分才是自己经过查阅资料和其他学者的学习笔记,结合个人理解总结成的原创内容。
| 原文 | The Elements of Statistical Learning |
|---|---|
| 翻译 | szcf-weiya |
| 时间 | 2018-08-21 |
| 解读 | Hytn Chen |
| 更新 | 2020-02-12 |
有 p>1p > 1p>1 个输入的线性模型 (3.1) 称作 多重线性回归模型.用单 (p=1p=1p=1) 变量线性模型的估计能更好理解模型 (3.6)(3.6)(3.6) 的最小二乘估计,我们将在这节中指出.
首先假设我们有一个没有截距的单变量模型,也就是
Y=Xβ+ε(3.23) Y=X\beta + \varepsilon \tag{3.23} Y=Xβ+ε(3.23)
最小二乘估计和残差为
β^=∑1Nxiyi∑1Nxi2ri=yi−xiβ^(3.24) \begin{aligned} \hat{\beta}&=\dfrac{\sum_1^Nx_iy_i}{\sum_1^Nx_i^2}\\ r_i &= y_i -x_i\hat{\beta} \end{aligned} \tag{3.24} β^ri=∑1Nxi2∑1Nxiyi=yi−xiβ^(3.24)
为了简便用向量表示,我们令 y=(y1,…,yN)T\mathbf{y}=(y_1,\ldots,y_N)^Ty=(y1,…,yN)T,x=(x1,…,xN)T\mathbf{x}=(x_1,\ldots,x_N)^Tx=(x1,…,xN)T,并且定义
⟨x,y⟩=∑i=1Nxiyi=xTy(3.25)
\begin{aligned}
\langle\mathbf{x},\mathbf{y}\rangle &= \sum\limits_{i=1}^Nx_iy_i\\
&=\mathbf{x^Ty}\tag{3.25}
\end{aligned}
⟨x,y⟩=i=1∑Nxiyi=xTy(3.25)
x\mathbf{x}x 和 y\mathbf{y}y 之间的内积,于是我们可以写成
β^=⟨x,y⟩⟨x,x⟩r=y−xβ^(3.26) \begin{aligned} \hat{\beta}&=\dfrac{\langle \mathbf{x,y}\rangle}{\langle\mathbf{x,x} \rangle}\\ \mathbf{r}&=\mathbf{y}-\mathbf{x}\hat{\beta} \end{aligned} \tag{3.26} β^r=⟨x,x⟩⟨x,y⟩=y−xβ^(3.26)
!!! note “weiya 注:原书脚注”
The inner-product notation is suggestive of generalizations of linear regression to different metric spaces, as well as to probability spaces. 内积表示是线性回归模型一般化到不同度量空间(包括概率空间)建议的方式.
正如我们所看到的,这个简单的单变量回归提供了多重线性回归的框架 (building block).进一步假设输入变量 x1,x2,…,xp\mathbf{x}_1,\mathbf{x_2,\ldots,x_p}x1,x2,…,xp(数据矩阵 X\mathbf{X}X 的列)是正交的;也就是对于所有的 j≠kj\neq kj=k 有⟨xj,xk⟩=0\langle \rm{x}_j,\rm{x}_k\rangle=0⟨xj,xk⟩=0.于是很容易得到多重最小二乘估计 β^j\hat{\beta}_jβ^j 等于 ⟨xj,y⟩/⟨xj,xj⟩\langle \mathbf{x}_j,\mathbf{y}\rangle/\langle\mathbf{x}_j,\mathbf{x}_j\rangle⟨xj,y⟩/⟨xj,xj⟩ ——单变量估计.换句话说,当输入变量为正交的,它们对模型中其它的参数估计没有影响.
正交输入变量经常发生于平衡的、设定好的实验(强制了正交),但是对于实验数据几乎不会发生.因此为了后面实施这一想法我们将要对它们进行正交化.进一步假设我们有一个截距和单输入 x\bf{x}x.则 x\bf{x}x 的最小二乘系数有如下形式
β^1=⟨x−xˉ1,y⟩⟨x−xˉ1,x−xˉ1⟩(3.27) \hat{\beta}_1=\dfrac{\langle \mathbf{x}-\bar{x}\mathbf{1},\mathbf{y}\rangle}{\langle \mathbf{x}-\bar{x}\mathbf{1},\mathbf{x}-\bar{x}\mathbf{1}\rangle}\tag{3.27} β^1=⟨x−xˉ1,x−xˉ1⟩⟨x−xˉ1,y⟩(3.27)
其中,xˉ=∑ixi/N\bar{x}=\sum_ix_i/Nxˉ=∑ixi/N,且 NNN 维单位向量 1=x0\mathbf{1}=x_01=x0.我们可以将式 (3.27)(3.27)(3.27) 的估计看成简单回归 (3.26)(3.26)(3.26) 的两次应用.这两步是:
在 1\bf{1}1 上回归 x\bf{x}x 产生残差 z=x−xˉ1\mathbf{z}=\mathbf{x}-\bar{x}\mathbf{1}z=x−xˉ1; 在残差 z\bf{z}z 上回归 y\bf{y}y 得到系数 β^1\hat{\beta}_1β^1在这个过程中,“在 a\bf{a}a 上回归 b\bf{b}b”意思是 b\bf{b}b 在 a\bf{a}a 上的无截距的简单单变量回归,产生系数 γ^=⟨a,b⟩/⟨a,a⟩\hat{\gamma}=\langle\mathbf{a,b}\rangle/\langle\mathbf{a,a}\rangleγ^=⟨a,b⟩/⟨a,a⟩ 以及残差向量 b−γ^a\mathbf{b}-\hat{\gamma}\mathbf{a}b−γ^a.我们称 b\bf{b}b 由 a\bf{a}a 校正(adjusted),或者关于 a\bf{a}a 正交化.
第一步对 x\mathbf{x}x 作关于 x0=1\mathbf{x}_0=\mathbf{1}x0=1 的正交化.第二步是一个利用正交预测变量 1\mathbf{1}1 和 z\mathbf{z}z 简单的单变量回归.图 3.4 展示了两个一般输入 x1\mathbf{x}_1x1 和 x2\mathbf{x}_2x2 的过程.正交化不会改变由 x1\mathbf{x}_1x1 和 x2\mathbf{x}_2x2 张成的子空间,它简单地产生一个正交基来表示子空间.
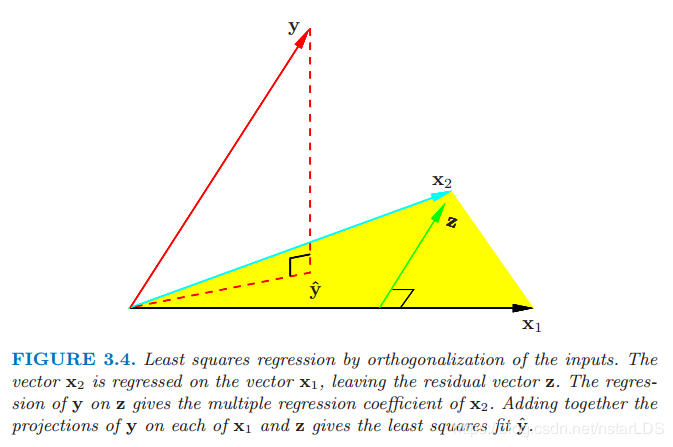
正交输入的最小二乘回归.向量 x2\mathbf{x}_2x2 在向量 x1\mathbf{x}_1x1 上回归,得到残差向量 z\mathbf{z}z.y\mathbf{y}y 在z\mathbf{z}z 上的回归给出 x2\mathbf{x}_2x2 的系数.把 y\mathbf{y}y 在 x1\mathbf{x}_1x1 和 z\mathbf{z}z 上的投影加起来给出了最小二乘拟合 y^\mathbf{\hat{y}}y^.
这个方法可以推广到 ppp 个输入的情形,如算法 3.1 所示.注意到第二步的输入 z_0,…,zj−1\mathbf{z}\_0,\ldots,\mathbf{z}_{j-1}z_0,…,zj−1 是正交的,因此这里计算得到的简单回归的系数实际上是多重回归的系数.

算法 3.1 依次正交的回归(施密特正交化)
初始化 z0=x0=1\mathbf{z}_0=\mathbf{x}_0=\mathbf{1}z0=x0=1 对于 j=1,2,…,pj=1,2,\ldots,pj=1,2,…,p在z0,z1,…,zj−1\mathbf{z}_0,\mathbf{z}_1,\ldots,\mathbf{z}_{j-1}z0,z1,…,zj−1上对xj\mathbf{x}_jxj回归得到系数γ^ℓj=⟨zℓ,xj⟩/⟨zℓ,zℓ⟩,ℓ=0,…,j−1\hat{\gamma}_{\ell j}=\langle \mathbf{z}_{\ell},\mathbf{x}_j \rangle/\langle\mathbf{z}_{\ell},\mathbf{z}_{\ell}\rangle,\ell=0,\ldots,j-1γ^ℓj=⟨zℓ,xj⟩/⟨zℓ,zℓ⟩,ℓ=0,…,j−1以及残差向量zj=xj−∑k=0j−1γ^kjzk\mathbf{z}_j=\mathbf{x}_j-\sum_{k=0}^{j-1}\hat{\gamma}_{kj}\mathbf{z}_kzj=xj−∑k=0j−1γ^kjzk 在残差zp\mathbf{z}_pzp上回归y\mathbf{y}y得到系数β^p\hat{\beta}_pβ^p
(Hytn注:一步步取有用的那个向量,就是和前面向量都正交的那个分向量)
算法的结果为
β^p=⟨zp,y⟩⟨zp,zp⟩(3.28) \hat{\beta}_p=\dfrac{\langle \mathbf{z}_p,\mathbf{y} \rangle}{\langle \mathbf{z}_p,\mathbf{z}_p \rangle}\tag{3.28} β^p=⟨zp,zp⟩⟨zp,y⟩(3.28)
对第二步中的残差进行重排列,我们可以看到每个 xj\mathbf x_jxj 是 zk,k≤j\mathbf z_k,k\le jzk,k≤j 的线性组合.因为 zj\mathbf z_jzj 是正交的,它们形成了 X\mathbf{X}X 列空间的基,从而得到最小二乘在该子空间上投影为 y^\hat{\mathbf{y}}y^.因为 zp\mathbf z_pzp仅与 xp\mathbf x_pxp 有关(系数为 1),则式 (3.28)(3.28)(3.28) 确实是 y\mathbf{y}y 在 xp\mathbf x_pxp 上多重回归的系数.
这一重要结果揭示了在多重回归中输入变量相关性的影响.注意到通过对 xj\mathbf x_jxj 重排列,其中的任何一个都有可能成为最后一个,然后得到一个类似的结果.因此一般来说,我们已经展示了多重回归的第 jjj 个系数是 y\mathbf{y}y 在 xj⋅012...(j−1)(j+1)...,p\mathbf x_{j\cdot 012...(j-1)(j+1)...,p}xj⋅012...(j−1)(j+1)...,p 的单变量回归,xj⋅012...(j−1)(j+1)...,p\mathbf x_{j\cdot 012...(j-1)(j+1)...,p}xj⋅012...(j−1)(j+1)...,p 是 xj\mathbf x_jxj 在x0,x1,...,xj−1,j+1,...,xp\mathbf x_0,\mathbf x_1,...,\mathbf x_{j-1},\mathbf{j+1},...,\mathbf{x}_px0,x1,...,xj−1,j+1,...,xp 回归后的残差向量:
多重回归系数 β^j\hat\beta_jβ^j 表示 xj\mathbf x_jxj 经过 x0,x1,…,xj−1,xj+1,…,xp\mathbf x_0,\mathbf x_1,\ldots,\mathbf x_{j-1},\mathbf x_{j+1},\ldots,\mathbf x_px0,x1,…,xj−1,xj+1,…,xp 调整后 xj\mathbf x_jxj 对 y\mathbf yy 额外的贡献
如果 xp\mathbf{x}_pxp 与某些 xk\mathbf{x}_kxk 高度相关,残差向量 zp\mathbf{z}_pzp 会近似等于 0,而且由(3.28)(3.28)(3.28)得到的系数 β^p\hat{\beta}_pβ^p 会非常不稳定.对于相关变量集中所有的变量都是正确的.在这些情形下我们可能得到所有的 Z 分数(如表 3.2 所示)都很小——相关变量集中的任何一个变量都可以删掉——然而我们不可能删掉所有的变量.由 (3.28)(3.28)(3.28) 我们也得到估计方差 (3.28)(3.28)(3.28) 的另一种方法
Var(β^p)=σ2⟨zp,zp⟩=σ2∥zp∥2(3.29)
\rm{Var}(\hat{\beta}_p)=\dfrac{\sigma^2}{\langle \mathbf{z}_p,\mathbf{z}_p \rangle}=\dfrac{\sigma^2}{\Vert\mathbf{z}_p\Vert ^2}\tag{3.29}
Var(β^p)=⟨zp,zp⟩σ2=∥zp∥2σ2(3.29)
换句话说,我们估计 β^p\hat{\beta}_pβ^p 的精度取决于残差向量 zp\mathbf{z}_pzp 的长度;它表示 xp\mathbf{x}_pxp 不能被其他 xk\mathbf{x}_kxk 解释的程度.
算法 3.1 被称作多重回归的 Gram-Schmidt 正交化,也是一个计算估计的有用的数值策略.我们从中不仅可以得到 β^p\hat{\beta}_pβ^p,而且可以得到整个多重最小二乘拟合,如练习 3.4 所示.
!!! info “weiya 注:Ex. 3.4”
已解决,详见 Issue 72: Ex. 3.4.
我们可以用矩阵形式来表示算法 3.1 的第二步:
X=ZΓ(3.30) \mathbf{X=Z\Gamma}\tag{3.30} X=ZΓ(3.30)
其中 Z\mathbf{Z}Z 是 zj\mathbf{z_j}zj(按顺序)作为列向量的矩阵,Γ\mathbf{\Gamma}Γ 是值为 γ^kj\hat\gamma_{kj}γ^kj 的上三角矩阵.引入第 jjj 个对角元 Djj=∥zj∥D_{jj}=\Vert \mathbf{z}_j \VertDjj=∥zj∥ 的对角矩阵 D\mathbf{D}D,我们有
X=ZD−1DΓ=QR(3.31)
\begin{aligned}
\mathbf{X}&=\mathbf{ZD^{-1}D\Gamma}\\
&=\mathbf{QR}\tag{3.31}
\end{aligned}
X=ZD−1DΓ=QR(3.31)
称为矩阵 X\mathbf{X}X 的 QR 分解.这里 Q\mathbf{Q}Q 为 N×(p+1)N\times (p+1)N×(p+1) 正交矩阵,QTQ=I\mathbf{Q^TQ=I}QTQ=I,并且 R\mathbf{R}R 为 (p+1)×(p+1)(p+1)\times (p+1)(p+1)×(p+1) 上三角矩阵.
QR\mathbf{QR}QR 分解表示了 X\mathbf{X}X 列空间的一组方便的正交基.举个例子,很容易可以看到,最小二乘的解由下式给出
β^=R−1QTyy^=QQTy(3.33)
\begin{aligned}
\hat{\beta}&=\mathbf{R^{-1}Q^Ty} \\
\hat{\mathbf{y}}&=\mathbf{QQ^Ty}\tag{3.33}
\end{aligned}
β^y^=R−1QTy=QQTy(3.33)
等式 (3.32) 很容易求解,因为 R\mathbf{R}R 为上三角(练习 3.4)
!!! info “weiya 注:Ex. 3.4”
已解决,详见 Issue 72: Ex. 3.4.
首先对于参数β^\hat \betaβ^的估计源于下面式子的变形:
(XTX)−1=(∑i=1Nxi2)−1 and XTY=∑i=1Nxiyi
\left(X^{T} X\right)^{-1}=\left(\sum_{i=1}^{N} x_{i}^{2}\right)^{-1} \quad \text { and } \quad X^{T} Y=\sum_{i=1}^{N} x_{i} y_{i}
(XTX)−1=(i=1∑Nxi2)−1 and XTY=i=1∑Nxiyi
结合前面章节一直提及的有关β^\hat \betaβ^的表达式,很容易得出式(3.24)(3.24)(3.24)。
那么如何进一步分析该式,其细节的推导如下所示:
XTX=[x1Tx2T⋮xpT][x1x2⋯xp]=[x1Tx1x1Tx2⋯x1Txpx2Tx1x2Tx2⋯x2Txp⋮⋮⋯⋮xpTx1xpTx2⋯xpTxp]=[x1Tx10⋯00x2Tx2⋯0⋮⋮⋯⋮00⋯xpTxp]=D
\begin{aligned}
X^{T} X &=\left[\begin{array}{c}
{x_{1}^{T}} \\
{x_{2}^{T}} \\
{\vdots} \\
{x_{p}^{T}}
\end{array}\right]\left[\begin{array}{llll}
{x_{1}} & {x_{2}} & {\cdots} & {x_{p}}
\end{array}\right]\\
&=\left[\begin{array}{cccc}
{x_{1}^{T} x_{1}} & {x_{1}^{T} x_{2}} & {\cdots} & {x_{1}^{T} x_{p}} \\
{x_{2}^{T} x_{1}} & {x_{2}^{T} x_{2}} & {\cdots} & {x_{2}^{T} x_{p}} \\
{\vdots} & {\vdots} & {\cdots} & {\vdots} \\
{x_{p}^{T} x_{1}} & {x_{p}^{T} x_{2}} & {\cdots} & {x_{p}^{T} x_{p}}
\end{array}\right]\\
&=\left[\begin{array}{cccc}
{x_{1}^{T} x_{1}} & {0} & {\cdots} & {0} \\
{0} & {x_{2}^{T} x_{2}} & {\cdots} & {0} \\
{\vdots} & {\vdots} & {\cdots} & {\vdots} \\
{0} & {0} & {\cdots} & {x_{p}^{T} x_{p}}
\end{array}\right]=D
\end{aligned}
XTX=⎣⎢⎢⎢⎡x1Tx2T⋮xpT⎦⎥⎥⎥⎤[x1x2⋯xp]=⎣⎢⎢⎢⎡x1Tx1x2Tx1⋮xpTx1x1Tx2x2Tx2⋮xpTx2⋯⋯⋯⋯x1Txpx2Txp⋮xpTxp⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡x1Tx10⋮00x2Tx2⋮0⋯⋯⋯⋯00⋮xpTxp⎦⎥⎥⎥⎤=D
那么β^\hat \betaβ^的估计值就是:
β^=D−1(XTY)=D−1[x1Tyx2Ty⋮xpTy]=[x1Tyx1Tx1x2Tyx2Tx2⋮xpTyxpTxp]
\begin{aligned}
\hat{\beta}&=D^{-1}\left(X^{T} Y\right)\\
&=D^{-1}\left[\begin{array}{c}
{x_{1}^{T} y} \\
{x_{2}^{T} y} \\
{\vdots} \\
{x_{p}^{T} y}
\end{array}\right]=\left[\begin{array}{c}
{\frac{x_{1}^{T} y}{x_{1}^{T} x_{1}}} \\
{\frac{x_{2}^{T} y}{x_{2}^{T} x_{2}}} \\
{\vdots} \\
{\frac{x_{p}^{T} y}{x_{p}^{T} x_{p}}}
\end{array}\right]
\end{aligned}
β^=D−1(XTY)=D−1⎣⎢⎢⎢⎡x1Tyx2Ty⋮xpTy⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎡x1Tx1x1Tyx2Tx2x2Ty⋮xpTxpxpTy⎦⎥⎥⎥⎥⎥⎥⎤
之后的文字看似复杂,其实总结起来做的事情就是:如何把yyy直接回归到X\rm{X}X张成的空间上去?直接进行最小二乘回归可以,如果X\rm{X}X线性无关但不正交(两者区别要明确,举例就是分别在平行两个平面里的两条直线,线性无关但不一定正交),那么每一组X\rm{X}X则有可能互相影响彼此项的系数。这时候就对X\rm{X}X张成的空间提取出该空间的正交基,就是所有基向量。如何实现这样的提取呢?就是采用施密特正交化。图3.4例举了yyy如何通过正交化之后的向量投影到二维空间上,多维也是如此思想。
施密特正交有助于帮助我们这样来估计函数值:
f^(x)=∑i=0pβ^i(ziTx)
\hat{f}(\mathbf{x})=\sum_{i=0}^{p} \hat{\beta}_{i}\left(\mathbf{z}_{i}^{T} \mathbf{x}\right)
f^(x)=i=0∑pβ^i(ziTx)
最终方差的计算式推导过程为
Var(β^p)=Var(zpTy⟨zp,zp⟩)=zpTVar(y)zp⟨zp,zp⟩2=zpT(σ2I)zp⟨zp,zp⟩2=σ2⟨zp,zp⟩
\begin{aligned}
\operatorname{Var}\left(\hat{\beta}_{p}\right) &=\operatorname{Var}\left(\frac{z_{p}^{T} y}{\left\langle z_{p}, z_{p}\right\rangle}\right)=\frac{z_{p}^{T} \operatorname{Var}(y) z_{p}}{\left\langle z_{p}, z_{p}\right\rangle^{2}}=\frac{z_{p}^{T}\left(\sigma^{2} I\right) z_{p}}{\left\langle z_{p}, z_{p}\right\rangle^{2}} \\
&=\frac{\sigma^{2}}{\left\langle z_{p}, z_{p}\right\rangle}
\end{aligned}
Var(β^p)=Var(⟨zp,zp⟩zpTy)=⟨zp,zp⟩2zpTVar(y)zp=⟨zp,zp⟩2zpT(σ2I)zp=⟨zp,zp⟩σ2
对于QR分解部分还有第二种解读,首先需要明确施密特正交化的原理。对可逆矩阵A的列向量组α1,α2,…αn\alpha_{1}, \alpha_{2}, \ldots \alpha_{n}α1,α2,…αn进行施密特正交化,最终标准正交向量的值是这样的:
ε1=β1∥β1∥=t11α1ε2=β2∥β2∥=t12α1+t22α2⋮εj=βj∥βj∥=t1jα1+t2jα2+…+tj−1,jαj−1+tj,jαj
\begin{aligned}
\varepsilon_{1} &=\frac{\beta_{1}}{\left\|\beta_{1}\right\|}=t_{11} \alpha_{1} \\
\varepsilon_{2} &=\frac{\beta_{2}}{\left\|\beta_{2}\right\|}=t_{12} \alpha_{1}+t_{22} \alpha_{2} \\
& \vdots \\
\varepsilon_{j} &=\frac{\beta_{j}}{\left\|\beta_{j}\right\|}=t_{1 j} \alpha_{1}+t_{2 j} \alpha_{2}+\ldots+t_{j-1, j} \alpha_{j-1}+t_{j, j} \alpha_{j}
\end{aligned}
ε1ε2εj=∥β1∥β1=t11α1=∥β2∥β2=t12α1+t22α2⋮=∥βj∥βj=t1jα1+t2jα2+…+tj−1,jαj−1+tj,jαj
用矩阵的形式表达就是:
(ε1,ε2,…,εj)=(α1,α2,…αn)[t11⋯t1n⋱⋮tnn]
\left(\varepsilon_{1}, \varepsilon_{2}, \ldots, \varepsilon_{j}\right)=\left(\alpha_{1}, \alpha_{2}, \ldots \alpha_{n}\right)\left[\begin{array}{ccc}
{t_{11}} & {\cdots} & {t_{1 n}} \\
{} & {\ddots} & {\vdots} \\
{} & {} & {t_{nn}}
\end{array}\right]
(ε1,ε2,…,εj)=(α1,α2,…αn)⎣⎢⎡t11⋯⋱t1n⋮tnn⎦⎥⎤
令
A=(α1,α2,…αn),Q=(ε1,ε2,…,εj)
A=\left(\alpha_{1}, \alpha_{2}, \ldots \alpha_{n}\right), Q=\left({\varepsilon_{1}}, \varepsilon_{2}, \ldots, \varepsilon_{j}\right)
A=(α1,α2,…αn),Q=(ε1,ε2,…,εj)
再记R=T−1R=T^{-1}R=T−1,即可得出结果A=QRA=QRA=QR,这里TTT的逆矩阵仍然是上三角阵。这里需要注意书中的逻辑是用减号,这里的QQQ得是标准正交基,因此书中采用DDD来给QQQ进行标准化。
求解得到QQQ和RRR之后,再推导最小二乘的系数和预测值的过程就比较简单,具体如下:
β^=(XTX)−1XTy=(RTQTQR)−1RTQTy=(RTR)−1RTQTy=R−1R−TRTQTy=R−1QTy
\begin{aligned}
\hat{\beta} &=\left(X^{T} X\right)^{-1} X^{T} \mathbf{y} \\
&=\left(R^{T} Q^{T} Q R\right)^{-1} R^{T} Q^{T} \mathbf{y} \\
&=\left(R^{T} R\right)^{-1} R^{T} Q^{T} \mathbf{y} \\
&=R^{-1} R^{-T} R^{T} Q^{T} \mathbf{y} \\
&=R^{-1} Q^{T} \mathbf{y}
\end{aligned}
β^=(XTX)−1XTy=(RTQTQR)−1RTQTy=(RTR)−1RTQTy=R−1R−TRTQTy=R−1QTy
以及
y^=Xβ^=QRR−1QTy=QQTy
\hat{\mathbf{y}}=X \hat{\beta}=Q R R^{-1} Q^{T} \mathbf{y}=Q Q^{T} \mathbf{y}
y^=Xβ^=QRR−1QTy=QQTy
证毕。
假设有多重输出 Y1,Y2,…,YKY_1,Y_2,\ldots,Y_KY1,Y2,…,YK,我们希望通过输入变量 X0,X1,X2,…,XpX_0,X_1,X_2,\ldots,X_pX0,X1,X2,…,Xp 去预测.我们假设对于每一个输出变量有线性模型
Yk=β0k+∑j=1pXjβjk+εk=fk(X)+εk(3.35) \begin{aligned} Y_k&=\beta_{0k}+\sum\limits_{j=1}^pX_j\beta_{jk}+\varepsilon_k \\ &= f_k(X)+\varepsilon_k \tag{3.35} \end{aligned} Yk=β0k+j=1∑pXjβjk+εk=fk(X)+εk(3.35)
有 NNN 个训练情形时我们可以将模型写成矩阵形式
Y=XB+E(3.36) \mathbf{Y=XB+E}\tag{3.36} Y=XB+E(3.36)
这里 Y\mathbf{Y}Y 为 N×KN\times KN×K 的响应矩阵,ikikik 处值为 yiky_{ik}yik,X\mathbf{X}X 为 N×(p+1)N\times (p+1)N×(p+1) 的输入矩阵,B\mathbf{B}B 为 (p+1)×K(p+1)\times K(p+1)×K 的系数矩阵 E\mathbf{E}E 为 N×KN\times KN×K 的误差矩阵.单变量损失函数 \eqref{3.2} 的直接推广为
RSS(B)=∑k=1K∑i=1N(yik−fk(xi))2=tr[(Y−XB)T(Y−XB)](3.38)
\begin{aligned}
\rm{RSS}(\mathbf{B})&=\sum\limits_{k=1}^K\sum\limits_{i=1}^N(y_{ik}-f_k(x_i))^2\\
&= \rm{tr}[\mathbf{(Y-XB)^T(Y-XB)}]\tag{3.38}
\end{aligned}
RSS(B)=k=1∑Ki=1∑N(yik−fk(xi))2=tr[(Y−XB)T(Y−XB)](3.38)
最小二乘估计有和前面一样的形式
B^=(XTX)−1XTY(3.39) \mathbf{\hat{B}=(X^TX)^{-1}X^TY}\tag{3.39} B^=(XTX)−1XTY(3.39)
因此第 kkk 个输出的系数恰恰是 yk\mathbf{y}_kyk 在 x0,x1,…,xp\mathbf{x}_0,\mathbf{x}_1,\ldots,\mathbf{x}_px0,x1,…,xp 上回归的最小二乘估计.多重输出不影响其他的最小二乘估计.
如果式 \eqref{3.34} 中的误差 ε=(ε1,…,εK)\varepsilon = (\varepsilon_1,\ldots,\varepsilon_K)ε=(ε1,…,εK) 相关,则似乎更恰当的方式是修正 \eqref{3.37} 来改成多重变量版本.特别地,假设 Cov(ε)=Σ\rm{Cov}(\varepsilon)=\SigmaCov(ε)=Σ,则 多重变量加权准则 为
RSS(B;Σ)=∑i=1N(yi−f(xi))TΣ−1(yi−f(xi))(3.40) \rm{RSS}(\mathbf{B;\Sigma})=\sum\limits_{i=1}^N(y_i-f(x_i))^T\Sigma^{-1}(y_i-f(x_i))\tag{3.40} RSS(B;Σ)=i=1∑N(yi−f(xi))TΣ−1(yi−f(xi))(3.40)
这可以由 多变量高斯定理 自然得出.这里 f(x)f(x)f(x) 为向量函数 (f1(x),…,fK(x))(f_1(x),\ldots,f_K(x))(f1(x),…,fK(x)),而且 yiy_iyi 为观测值 iii 的 KKK 维响应向量.然而,可以证明解也是由式 \eqref{3.39} 给出;KKK 个单独的回归忽略了相关性(练习 3.11).如果 Σi\Sigma_iΣi 对于不同观测取值不同,则不再是这种情形,而且关于 B\mathbf{B}B 的解不再退化 (decouple).
!!! info “weiya 注:Ex. 3.11”
已解决,详见 Issue 73: Ex. 3.11.
在 3.7 节我们继续讨论多重输出的问题,并且考虑需要合并回归的情形.
作者:Nstar-LDS