Python数据拟合实现最小二乘法示例解析

Natalie ·

更新时间:2024-09-21

· 491 次阅读

线性拟合

高阶多项式

多自变量

指数函数

所谓最小二乘法，即通过对数据进行拟合，使得拟合值与样本值的方差最小。

线性拟合

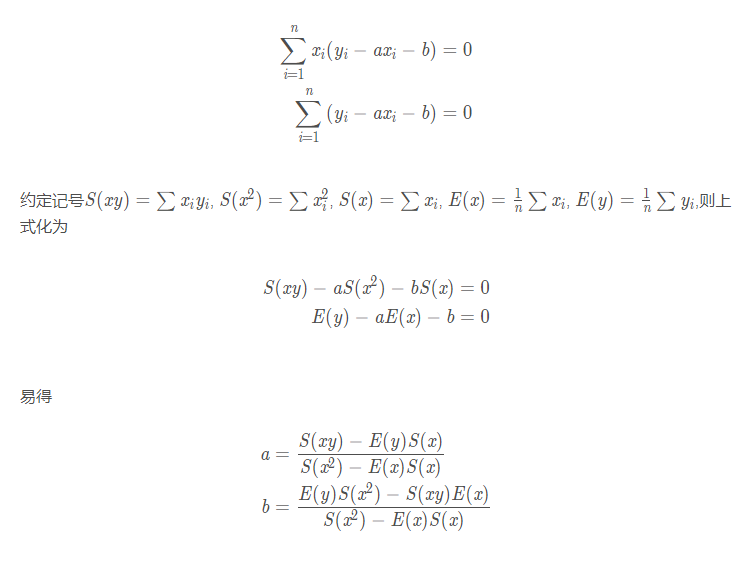
这个表达式还是非常简单的。

对于有些情况，我们往往选取自然序列作为自变量，这个时候在求自变量的取值时可以用到一些初等数学的推论，对于 x ∈ [ m , n ] 的自然序列来说，有


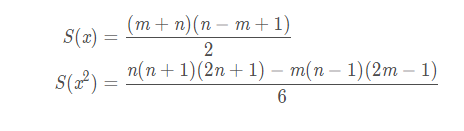
#文件名core.py
import numpy as np
def leastSquare(x,y):
    if len(x)==2:
    #此时x为自然序列
        sx = 0.5*(x[1]-x[0]+1)*(x[1]+x[0])
        ex = sx/(x[1]-x[0]+1)
        sx2 = ((x[1]*(x[1]+1)*(2*x[1]+1))
              -(x[0]*(x[0]-1)*(2*x[0]-1)))/6
        x = np.array(range(x[0],x[1]+1))
    else:
        sx = sum(x)
        ex = sx/len(x)
        sx2 = sum(x**2)    
    sxy = sum(x*y)
    ey = np.mean(y)
    a = (sxy-ey*sx)/(sx2-ex*sx)
    b = (ey*sx2-sxy*ex)/(sx2-ex*sx)
    return a,b

测试一下


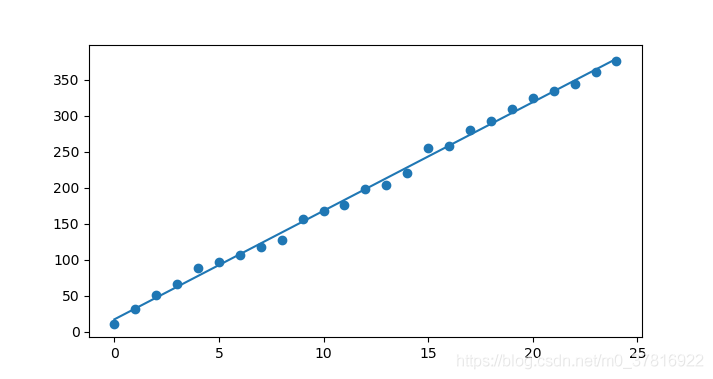
>>> x = np.arange(25)
>>> y = x*15+20+np.random.randn(len(x))*5#randn生成正态分布噪声
>>> a,b = core.leastSquare(x,y)
>>> plt.scatter(x,y)#原始数据散点图
<matplotlib.collections.PathCollection object at 0x00000218DEBBEDC8>
>>> plt.plot(x,a*x+b)#拟合直线
[<matplotlib.lines.Line2D object at 0x00000218E0314FC8>]
>>> plt.show()

得到

高阶多项式

和前面一样，约定

代码如下


#传入参数格式为np.array,n为阶数
def leastSquareMulti(x,y,n):
    X = [np.sum(x**i) for i in range(2*n+1)]
    Y = np.array([[np.sum(y*x**i)] for i in range(n+1)])
    S = np.array([X[i:i+n+1] for i in range(n+1)])
    return np.linalg.solve(S,Y)#

经测试结果如下：


>>> x = np.arange(25)
>>> y = x**3+3*x**2+2*x+12
>>> import core
>>> core.leastSquareMulti(x,y,3)
array([[12.],#此为常数项
       [ 2.],
       [ 3.],
       [ 1.]])

多自变量

对于样本

则相应地其误差方程组可表示为

指数函数

则其代码为


def expFit(x,y):
    y0 = y[0:-3]
    y1 = y[1:-2]
    y2 = y[2:-1]
    B,C = leastSquare(y2/y0,y1/y0)
    b1 = np.log((B-np.sqrt(B**2+4*C))/2)
    b2 = np.log((B+np.sqrt(B**2+4*C))/2)
    X = np.exp(b1-b2)*x
    Y = y/np.exp(b2*x)
    a1,a2 = leastSquare(X,Y)
    return a1,a2,b1,b2

以上就是Python数据拟合实现最小二乘法示例解析的详细内容，更多关于Python实现最小二乘法的资料请关注软件开发网其它相关文章！

示例最小二乘法 Python

1024 个赞