python：绘制直方图（Histogram）

Kamaria ·

更新时间:2024-11-01

· 585 次阅读

简介

本文主要总结如何绘制直方图，以及常用的使用场景。

什么是直方图：一个随机变量在各个取值区间有个概率分布，将其绘制出来：x轴为等间隔的取值区间(bins)，y轴为该区间的频数(可归一化)，即直方图。

接口

Signature:
plt.hist(
    x,
    bins=None,
    range=None,
    density=None,
    weights=None,
    cumulative=False,
    bottom=None,
    histtype='bar',
    align='mid',
    orientation='vertical',
    rwidth=None,
    log=False,
    color=None,
    label=None,
    stacked=False,
    normed=None,
    *,
    data=None,
    **kwargs,
)
Docstring:
Plot a histogram.
Compute and draw the histogram of *x*. The return value is a
tuple (*n*, *bins*, *patches*) or ([*n0*, *n1*, ...], *bins*,
[*patches0*, *patches1*,...]) if the input contains multiple
data.

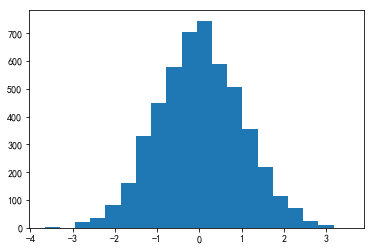
实例1：正态分布的直方图

实例
生成一个正态分布数据x，然后绘制其直方图。
代码

mu,sigma = 0,1
x = np.random.normal(mu,sigma,size=5000)
n, bins,patches = plt.hist(x,bins=20)
print('n:',n)
print('bins:',bins)
print('patches:',patches)

分析
输入参数：

x：即随机变量的取值数据 bins：表示将x等间隔分成多少个区间。比如这里分成了20个区间，具体说：它是将[min(x),max(x)]这个范围等间隔分成20个区间(bin)，即有21个区间端点。

返回参数：

n：各区间(bin)的频数，即20个柱子的高度， bins：21个区间端点。查看数值可以看到第一个端点为min(x)，最后一个端点为max(x)。 patches：表示20个柱子

结果

n: [  2.   1.  22.  36.  81. 161. 329. 448. 580. 703. 745. 590. 507. 354.
 217. 115.  73.  25.  10.   1.]
bins: [-3.66700533 -3.30660994 -2.94621455 -2.58581916 -2.22542377 -1.86502838
 -1.50463298 -1.14423759 -0.7838422  -0.42344681 -0.06305142  0.29734397
  0.65773937  1.01813476  1.37853015  1.73892554  2.09932093  2.45971632
  2.82011172  3.18050711  3.5409025 ]
patches:

原创文章 57获赞 38访问量 32万+ 关注私信展开阅读全文
作者：kaever