机器学习推导+python实现（九）：线性支持向量机

写在开头：今天将跟着昨天的节奏来分享一下线性支持向量机。

线性回归（一）、逻辑回归（二）、K近邻（三）、决策树值ID3（四）、CART（五）、感知机（六）、神经网络（七）、线性可分支持向量机（八）、线性支持向量机（九）、线性不可分支持向量机（十）、朴素贝叶斯（十一）、Lasso回归（十二）、Ridge岭回归（十三）等。
昨天再分享线性可分支持向量机的时候，大家不免会发现其既定前提是数据线性可分，但实际生活中对于线性可分的数据来说还是比较少，那么如何在线性可分支持向量机的基础上进行改机使得线性支持向量机能够在线性不可分的数据中绘制超平面进行分类任务。这就是我们今天要分享的线性支持向量机。

同样我们尽量采用提问的方式来对模型进行探索，模型参考《统计学习方法（第二版）》。
Q1：如何在线性不可分数据中使用线性支持向量机？
在上一节中，我们对数据采用的最大间隔法会使得所有数据都在分离超平面的距离1之外，那么如果训练数据中无法找到满足与分离超平面间隔1的点怎么办。这是我们就需要把上一节中类似于硬间隔最大化改为软间隔最大化，也就是使得我们的间隔边界可动，不再是固定的1。为了实现这个想法，我们需要引入松弛变量来使得间隔边间进行外扩，加入松弛变量后就会使得函数间隔大于等于1，约束条件变为，
yi(w⋅xi+b)⩾1−ξiy_i(w\cdot x_i+b)\geqslant 1-\xi_iyi​(w⋅xi​+b)⩾1−ξi​然后为了避免加入一个过大的ξi\xi_iξi​，这里在目标函数处添加一个代价项，
12(∣∣w∣∣)2+C∑i=1Nξi\frac{1}{2}(||w||)^2+C\sum \limits_{i=1}^{N}\xi_i21​(∣∣w∣∣)2+Ci=1∑N​ξi​C在这里成为惩罚参数，C值大当ξi\xi_iξi​增加，代价项就会增大很多，也就是对于ξi\xi_iξi​的变化越敏感。又因为之前讨论过这里是求目标函数的最小值，所以如果增加过大的ξi\xi_iξi​就会使得目标函数变大，于是目标函数的左右两项就是一个博弈的过程，寻找到一个满足约束条件的最优解。
于是我们加入松弛变量的凸二次规划问题如下，因为这仍然是一个凸二次规划问题，所以可以证明w,bw,bw,b有解，但bbb有可能不是唯一解，
min⁡w,b,ξ12(∣∣w∣∣)2+C∑i=1Nξis.t.    yi(w⋅xi+b)⩾1−ξi,  i=1,2,…,N    ξi>=0,  i=1,2,…,N\begin{aligned} {\underset {w,b,\xi}{\operatorname {min} }} &\quad\frac{1}{2}(||w||)^2+C\sum \limits_{i=1}^{N}\xi_i \\ s.t.&\ \ \ \ y_i(w\cdot x_i+b)\geqslant 1-\xi_i,\ \ i=1,2,\dots,N\\ &\ \ \ \ \xi_i>=0,\ \ i=1,2,\dots,N \end{aligned}w,b,ξmin​s.t.​21​(∣∣w∣∣)2+Ci=1∑N​ξi​    yi​(w⋅xi​+b)⩾1−ξi​,  i=1,2,…,N    ξi​>=0,  i=1,2,…,N​Q2：该方法也有对偶算法吗
对于凸二次优化都是有一种对偶算法可以进行求解的，首先仍然需要构造拉格朗日函数，然后对拉格朗日函数求偏导设为0，并将最后的结果带回式子中，与上一节方法类似。首先构造拉格朗日函数，(这里勒格朗日函数中间项的减号是因为约束条件是大于等于0，需要添加符号变为小于等于0。对于求和号是因为一个样本点就算一个约束，于是就有N个约束一起计算需要求和)
L(w,b,ξ,a,u)=12(∣∣w∣∣)2+C∑i=1Nξi−∑i=1Nai(yi(w⋅xi+b)−1+ξi)−∑i=1NuiξiL(w,b,\xi,a,u)=\frac{1}{2}(||w||)^2+C\sum \limits_{i=1}^{N}\xi_i -\sum \limits_{i=1}^{N}a_i(y_i(w\cdot x_i+b)-1+\xi_i)-\sum \limits_{i=1}^{N}u_i\xi_iL(w,b,ξ,a,u)=21​(∣∣w∣∣)2+Ci=1∑N​ξi​−i=1∑N​ai​(yi​(w⋅xi​+b)−1+ξi​)−i=1∑N​ui​ξi​然后分别对其中的参数进行求偏导，
∇wL(w,b,ξ,a,u)=w−∑i=1Naiyixi=0\nabla_wL(w,b,\xi,a,u)=w-\sum\limits_{i=1}^{N}a_iy_ix_i=0∇w​L(w,b,ξ,a,u)=w−i=1∑N​ai​yi​xi​=0∇bL(w,b,ξ,a,u)=−∑i=1Naiyi=0 \nabla_bL(w,b,\xi,a,u)=-\sum\limits_{i=1}^{N}a_iy_i=0∇b​L(w,b,ξ,a,u)=−i=1∑N​ai​yi​=0∇ξL(w,b,ξ,a,u)=C−ai−ui=0 \nabla_{\xi}L(w,b,\xi,a,u)=C-a_i-u_i=0∇ξ​L(w,b,ξ,a,u)=C−ai​−ui​=0这里求导的前两项是与上一节的线性可分支持向量机的对偶算法形式一样，只是对于ξ\xiξ求偏导后多出了一个对拉格朗日系数的限制，于是得到，
w=∑i=1Naiyixiw=\sum\limits_{i=1}^{N}a_iy_ix_i w=i=1∑N​ai​yi​xi​∑i=1Naiyi=0\sum\limits_{i=1}^{N}a_iy_i=0 i=1∑N​ai​yi​=0C−ai−ui=0C-a_i-u_i=0C−ai​−ui​=0所以这里吧计算得到的三个式子带回之前的拉格朗日函数，这里的操作也和之前一样，就得到了对偶形式的目标函数，然后因为原问题是最小最大问题，所以对偶形式就为最大最小问题，里面的最小即对拉格朗日的极值，将最优解代入就可求得最小解，然后需要求外层的最大解，注意第下面的最后一个约束是对上面两个式子的总结，
max⁡a −12∑i=1N∑j=1Naiajyiyj(xi⋅xj)+∑i=1Nais.t.    ∑i=1Naiyi=0    C⩾ai⩾0,    i=1,2,…,N\begin{aligned} {\underset {a}{\operatorname {max} }}&\ -\frac{1}{2}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}a_ia_jy_iy_j(x_i\cdot x_j)+\sum\limits_{i=1}^{N}a_i \\ s.t.&\ \ \ \ \sum\limits_{i=1}^{N}a_i y_i=0\\ &\ \ \ \ C\geqslant a_i\geqslant0,\ \ \ \ i=1,2,\dots,N\\ \end{aligned}amax​s.t.​ −21​i=1∑N​j=1∑N​ai​aj​yi​yj​(xi​⋅xj​)+i=1∑N​ai​    i=1∑N​ai​yi​=0    C⩾ai​⩾0,    i=1,2,…,N​同样根据KKT条件，我们可以求得w∗,b∗w^*,b^*w∗,b∗两个的最优解，
w∗=∑i=1Nai∗yixiw^*=\sum\limits_{i=1}^{N}a_i^*y_ix_i w∗=i=1∑N​ai∗​yi​xi​b∗=yj−∑i=1Nai∗yi(xi⋅xj)b^*=y_j-\sum\limits_{i=1}^{N}a_i^*y_i(x_i\cdot x_j) b∗=yj​−i=1∑N​ai∗​yi​(xi​⋅xj​)具体证明过程可以见《统计学习方法（第二版）》，于是最后得到我们的分离超平面以及分类决策函数，
w∗⋅x+b∗=0w^*\cdot x+b^*=0w∗⋅x+b∗=0f(x)=sign(w∗⋅x+b∗)f(x)=sign(w^*\cdot x+b^*)f(x)=sign(w∗⋅x+b∗)Q3：在这个函数里的支持向量与线性可分里的一样吗？
从判断条件上来讲基本是一致的，都是对应于ai∗>0a^*_i>0ai∗​>0的样本点就成为支持向量，但是由于存在松弛变量，就会使得支持向量不一样就在间隔线上，而有可能在间隔线以内以及错误分类的那一面，但都不影响他为支持向量，因为本来就是用表现最差的一些数据来衡量整个算法。这里放一张参考书里面的图，从图上可以看到一些支持向量以及不再在间隔便边界上了。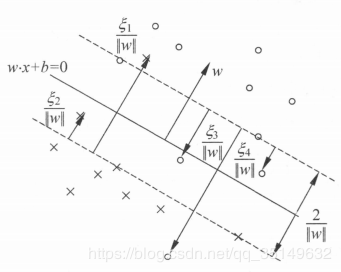
Q4:除了最大间隔，还要其他方法可以作为目标函数吗？
根据在机器学习里面的思想，一般是寻找损失函数的最小值，那么在这个原始问题里能否寻找到损失函数的最小值呢？通过书上的介绍可以知道，一种叫做合页损失函数，因为其图像形状就像书在翻页。
具体思路简单来说就是衡量数据划分后的损失，如果数据正确划分则无损失，如果数据错误划分则记损失为1−yi(w⋅xi+b)1-y_i(w\cdot x_i+b)1−yi​(w⋅xi​+b)，这里的思路正好和前面的方法不太一样，前面是把样本都分到正确的类的基础上，然后记录间隔有多大，也就是可信度有多大。这里的思路是选择一个损失最小的然后记录参数，这正是机器学习的通用思路。两种不同的思路正好都能解决问题，于是得到我们的最优化问题是，
min⁡w,b∑i=1N[1−yi(w⋅xi+b)]++λ∣∣w∣∣2\begin{aligned} {\underset {w,b}{\operatorname {min} }} &\quad\sum \limits_{i=1}^{N}[1-y_i(w\cdot x_i+b)]_++\lambda ||w||^2\\ \end{aligned}w,bmin​​i=1∑N​[1−yi​(w⋅xi​+b)]+​+λ∣∣w∣∣2​然后可以通过转化证明将[1−yi(w⋅xi+b)]+=ξi[1-y_i(w\cdot x_i+b)]_+=\xi_i[1−yi​(w⋅xi​+b)]+​=ξi​，证明过程可以查阅参考书，直观理解来看，式子左侧，如果大于0则说明样本点不是在间隔之内就是预测错误，需要添加ξi\xi_iξi​等大小的松弛变量，如果小于等于0那说明样本点在间隔线之外属于分类正确的点，于是就不需要添加ξi\xi_iξi​，所以两者效果相同可以进行替换。且如果再令λ=12C\lambda =\frac{1}{2C}λ=2C1​则可以得到，
min⁡w,b1C(C∑i=1Nξi+12(∣∣w∣∣)2)s.t.    yi(w⋅xi+b)⩾1−ξi,  i=1,2,…,N    ξi>=0,  i=1,2,…,N\begin{aligned} {\underset {w,b}{\operatorname {min} }} &\quad \frac{1}{C}(C\sum\limits_{i=1}^{N}\xi_i+\frac{1}{2}(||w||)^2)\\ s.t.&\ \ \ \ y_i(w\cdot x_i+b)\geqslant 1-\xi_i,\ \ i=1,2,\dots,N\\ &\ \ \ \ \xi_i>=0,\ \ i=1,2,\dots,N \end{aligned}w,bmin​s.t.​C1​(Ci=1∑N​ξi​+21​(∣∣w∣∣)2)    yi​(w⋅xi​+b)⩾1−ξi​,  i=1,2,…,N    ξi​>=0,  i=1,2,…,N​这个式子是不是很熟悉，没错目标函数就是原始问题的1C\frac{1}{C}C1​倍，所以其实最后想说的呢就是殊途同归，不管是用间隔最大法还是记录损失函数最后得到的形式都是一样的。
Q5:原始问题的目标函数与合页损失函数的目标函数相同吗？
但是需要注意一点的是，在原始问题中ξi\xi_iξi​是可以随意设置的，而在此处ξi\xi_iξi​是每个样本计算得到的定值，也就是设置最小的ξi\xi_iξi​。同样在原始问题的目标函数者能够是以12(∣∣w∣∣)2\frac{1}{2}(||w||)^221​(∣∣w∣∣)2为目标，因为ξi\xi_iξi​可以任意变动，所以加入其约束项。而在合页损失函数中，目标就是在w,bw,bw,b定下来后计算ξi\xi_iξi​表示误差的大小，而使用12(∣∣w∣∣)2\frac{1}{2}(||w||)^221​(∣∣w∣∣)2来作为正则项，避免函数的过拟合。所以即使是差不多的形式，其理解意思上也存在着主次的区别。

这里我们借鉴参考公众号思路，使用cvxpot包来解决凸优化的问题，这个包的安装需要提前安装numpy的mkl包，然后对于这个包的使用可以参考一下这里，其余的思路就是我们针对线性支持向量机的对偶形式进行python实现，这里我们不使用任何核函数的技巧，仅仅对对偶问题进行凸优化的解决。
首先第一步生成数据，这里生成数据就要比上一节的简单的随机数有意思一点点，这里使用的是正态分布的随机数生成，代码如下，

我们来看一下生成数据的规模，

再让我们看一下数据的分布吧，

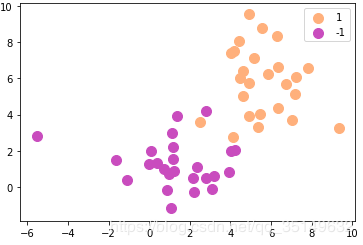
可以看到数据不再是线性可分的了，所以就不能再使用上一节的模型，这里我们用线性可分的模型来处理。这里是对对偶函数进行凸优化解决，

下面来看一下训练结果和效果咋样，

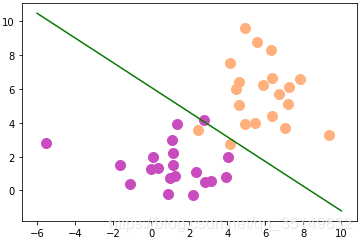
从训练集效果来看还不错哦，下面加入预测集来看看预测效果咋样呢，首先定义预测函数，

再来看一下整体的效果，并且加两跟间隔线，

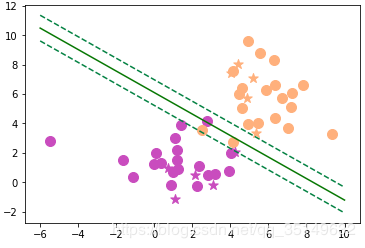
所以线性支持向量机能够在线性不可分的数据情况下，进行分了处理，当然存在着个别点是被误分类了的，但总体上是可以接受的，因为没有把间隔线再往前话，就有可能过拟合，这也是正则化的作用。好了按照惯例我们把整个模型封装起来吧。在封装的时候考虑到时候有C的出现，这样就可以用于线性可分与线性不可分的两种支持向量机了。