最优化理论实践——支持向量机
约束优化算法实现SVM
约束优化算法概述
作者:Hαlcyon
阅读文章前,我希望你应该知道约束优化问题的KKT条件,KKT条件能够给出一组方程,并且是最优解的必要条件,在这些解里做遍历并用二阶条件判断是一种解决问题的方式,但对一些并不容易计算的非线性方程组和hessian矩阵,这种方法并不高效。因此我们来介绍一些简单的解决一般约束优化问题的算法。







import numpy as np
import random
from copy import deepcopy
from matplotlib import pyplot as plt
这里使用0.1的起始γ,每次迭代倍增,最后将有3000以上的惩罚因子大小。学习率随γ的变化自动调整。
def Dot(x,y):
x = x.reshape(1,-1)
y = y.reshape(-1,1)
return x.dot(y)[0]
class SVM:
def __init__(self, dim):
'''
给定数据维度dim进行初始化
参数的初始化一般随机
'''
self.w = np.zeros(dim)
self.b = 0
self.support = []
def partial(self, X, Y, gamma, printing=False):
N,dim = X.shape;
dw = deepcopy(self.w)
db = 0;
for i in range(N):
if (printing):
print("x:",X[i])
print("y:",Y[i])
print(1-Y[i]*(Dot(self.w,X[i])+self.b))
if 1-Y[i]*(Dot(self.w,X[i])+self.b)=0)
return y*2-1
def show(self,a,b,X,Y):
#以现有的w和b打印划分平面,要求dim=2
if self.w.size!=2:
print("Dimension is not 2!")
return
x = np.linspace(a,b,num=100)
y = -self.w[0]/self.w[1]*x-self.b/self.w[1]
plt.plot(x,y,c='black')
plt.xlabel("x1")
plt.xlabel("x2")
plt.title("Support vector mechine by penalty method")
#同时,展示支撑向量,用+表示
sv = [None,None]
svdis = [0,0]
for i in range(len(X)):
if Y[i]==1:
cls = 0
else:
cls = 1
f = abs(Dot(self.w,X[i])+self.b)
if type(sv[cls])==type(None) or f<svdis[cls]:
sv[cls] = X[i]
svdis[cls] = f
plt.scatter(sv[0][0],sv[0][1],edgecolors='black',c='r',marker='+',linewidths=15)
plt.scatter(sv[1][0],sv[1][1],edgecolors='black',c='r',marker='+',linewidths=15)
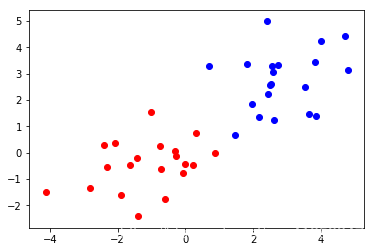
在均匀分布上使用高斯分布制造样本点,训练后的分类平面如下。
X11 = np.random.rand(20,1)
X12 = np.random.rand(20,1)
X11+=2;X12+=2
X11+=np.random.randn(20,1)
X12+=np.random.randn(20,1)
X1 = np.concatenate([X11,X12],axis =1)
X21 = np.random.rand(20,1)
X22 = np.random.rand(20,1)
X21-=1.5;X22-=1
X21+=np.random.randn(20,1)
X22+=np.random.randn(20,1)
X2 = np.concatenate([X21,X22],axis =1)
plt.scatter(X1[:,0].reshape(-1),X1[:,1].reshape(-1),c='b')
plt.scatter(X2[:,0].reshape(-1),X2[:,1].reshape(-1),c='r')
plt.show()
X = np.concatenate((X1,X2))
Y = np.array([1 for i in range(20)]+[-1 for i in range(20)])
svm = SVM(2)
svm.fit(X,Y)
Iteration: 0
W: [0.55302791 0.44010954]
b: -0.9099999999999999
Iteration: 1
W: [0.63101341 0.45857024]
b: -1.09
Iteration: 2
W: [0.72082093 0.57861661]
b: -1.3000000000000003
Iteration: 3
W: [0.8583813 0.65772783]
b: -1.7600000000000007
Iteration: 4
W: [0.94732829 0.7313659 ]
b: -1.8400000000000007
Iteration: 5
W: [1.18942914 0.91113098]
b: -2.05
Iteration: 6
W: [1.50525949 1.17111112]
b: -2.329999999999994
Iteration: 7
W: [1.82098084 1.41716943]
b: -2.639999999999989
Iteration: 8
W: [1.83692313 1.43355505]
b: -2.63999999999999
Iteration: 9
W: [1.83612493 1.43161008]
b: -2.6399999999999904
Iteration: 10
W: [1.82989512 1.43103962]
b: -2.6399999999999904
Iteration: 11
W: [1.82679169 1.43074295]
b: -2.6399999999999904
Iteration: 12
W: [1.83980108 1.43317587]
b: -2.639999999999991
Iteration: 13
W: [1.83755659 1.43142744]
b: -2.639999999999991
Iteration: 14
W: [1.83643537 1.43055403]
b: -2.639999999999991
plt.figure(figsize=(10, 6.5))
plt.scatter(X1[:,0].reshape(-1),X1[:,1].reshape(-1),c='w',edgecolors='g')
plt.scatter(X2[:,0].reshape(-1),X2[:,1].reshape(-1),c='w',edgecolors='b')
svm.show(-5,5,X,Y)
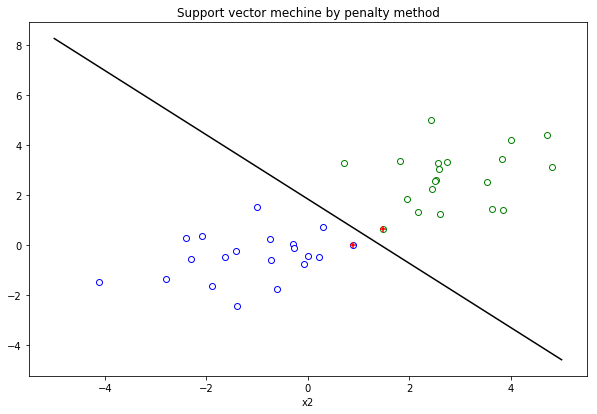
使用罚函数法训练超平面并不是一个高效的方法,更高效的方法是启发式的SMO算法,本实验实际上只是帮助我自己掌握并运用课程中学到的优化理论知识。更多有关机器学习的知识我将在本学期进行学习,欢迎关注。
作者:Hαlcyon