约瑟夫问题—JAVA语言分析解决。
约瑟夫问题:
作者:黑白帽子
据说著名犹太历史学家 Josephus有过以下的故事:在罗马人占领乔塔帕特后****,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从**。Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。**
问题转换:
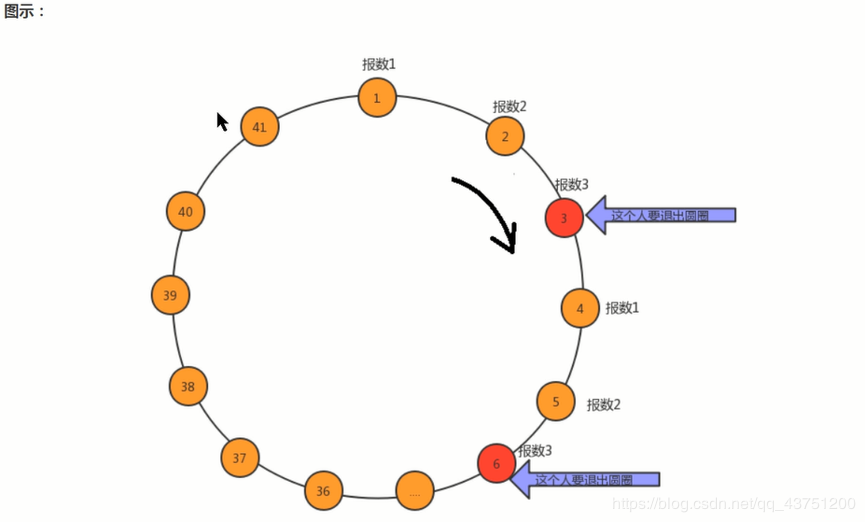
41个人坐一圈,第一个人编号为1,第二个人编号为2,第n个人的编号为n
1.编号为1的人开始从1报数,依次向后,报数为3的那个人退出圈。
2.自退出那个人开始的下一个人再次从1开始报数,依次类推。
3.求出最后退出的那个人的编号。
 解决思路:
解决思路:
1.构建含有41个结点的单向循环链表,分别存储1-41的值,分别代表这41个人;
2.使用计数器count,记录当前报数的值;
3,遍历链表,每循环一个,count++;
4.判断count的值,如果是3,则从链表中删除这个结点并且打印结点的值,把count重置为0;
代码试下如下:
public class JosephTest {
public static void main(String[] args) {
//解决约瑟夫问题
//1.构建循环链表,包含41个结点,分别存储1~41之间的值
//用来记录首结点
Node first = null;
//用来记录前一个结点,用于连接下一个结点
Node pre = null;
for (int i = 1; i <= 41; i++) {
///如果是第一个结点
if(i == 1){
first = new Node(i,null);
pre = first;
continue;
}
//如果不是第一个结点,利用pre连接下一个结点
Node newNode = new Node(i, null);
pre.next = newNode;
pre = newNode;
//构建循环的链表
if(i == 41){
pre.next = first;
}
}
//2.需要count计数器,模拟报数
int count = 0;
//3.遍历循环链表
//记录每次遍历拿到的结点,默认从首结点开始
Node n = first;
//记录当前结点的上一个结点
Node before = first;
while (n != n.next){
//模拟报数
count++;
//判断当前报数是不是3
if(count == 3){
//如果是3,则把当前结点删除打印当前结点,重置count= 0,让当前结点n后移
before.next = n.next;
System.out.print(n.item+",");
//n继续往后移
n = n.next;
//报数重置为0
count = 0;
}else {
//如果不是3,让before变为当前结点,让当前结点后移
before = n;
//n继续往后移
n = n.next;
}
}
//打印最后一个元素
System.out.println(n.item);
}
public static class Node{
//存储数据
T item;
//指向下一个结点
Node next;
public Node(T item,Node next){
this.item = item;
this.next = next;
}
}
}
程序运行结果截图:
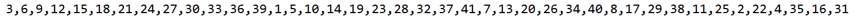
作者:黑白帽子