用python实现绘制Julia集与Mandelbrot集
前言
最近因为个人原因接触了分型图片,在查阅了大部分的资料后,终于成功呈现出分型图案,非常有成就感。这边最主要是借用了matplotlib和PIL两个库。
Mandelbrot集合与Julia集合都可以用复二次多项式f(z)=z2+cf(z) =z^{2}+ cf(z)=z2+c迭代得到:
Mandelbrot集合让初始的z0=0z_{0}=0z0=0,得到序列c,c2+c,(c2+c)2+c,... c,c^2+ c,(c^2+ c)^2+ c,...c,c2+c,(c2+c)2+c,...Julia集合则是给出一个固定c值决定它的形状,得到序列z,z2+c,(z2+c)2+c,...z,z^2+ c,(z^2+ c)^2+ c, ...z,z2+c,(z2+c)2+c,...(关于z与c是如何决定两种分型的形状可以参考看明白Julia集)
Mandelbrot集合与Julia集合都是一个复数的集合,给定复数c,在迭代后如果发散,它就不属于这个集合;如果停留在有限半径的圆盘内,它就属于这个集合。而由于函数的无穷,我们主要把 |z|<2并且在一定迭代数maxIter 下属于集合的c进行绘制。
我们通过对属于集合中的c们绘制上深浅颜色显得更加可观。
方法一Mandelbrot集合
def Mandelbrot():
w, h= 780, 520
bitmap = imag.new("RGB", (w, h), "white")
pix = bitmap.load()
maxIter = 255
for x in range(w):
for y in range(h):
zx,zy=0,0
#从z=0开始迭代
cx = 1.5 * (x - w / 2) / (w / 2)
cy = 1.0 * (y - h / 2) / (h / 2)
#宽高3:2主要是因为Mandelbrot集合图像范围
#主要在x区间(-1,2)y区间(-1,1)之间
#这两行代码主要是把像素坐标投射到复数范围
i = maxIter
#定义最大迭代数
while zx * zx + zy * zy 1:
#满足复数z的模|z|<2并且没有超过最大迭代数
tmp = zx * zx - zy * zy + cx
zy, zx = 2.0 * zx * zy + cy, tmp
i -= 1
pix[x, y] = (i << 21) + (i << 10) + i * 8
#这边用的是标准的RGB模式(0,0,0)~(255,255,255)
#为迭代次数i进行上色,255为(255,0,0),2^24为(0,0,255)
bitmap.save("1.png", "PNG")

Julia集合
def julia_set():
cX = round(random.uniform(-2, 2),5)
cY = round(random.uniform(-2, 2),5)
#随机生成固定区间的一个c值
w, h= 780, 520
bitmap = imag.new("RGB", (w, h), "white")
pix = bitmap.load()
maxIter = 255
for x in range(w):
for y in range(h):
zx =1.5*(x - w / 2)/(w / 2)
zy =1.0*(y - h / 2)/(h / 2)
i = maxIter
while zx * zx + zy * zy 1:
tmp = zx * zx - zy * zy + cX
zy, zx = 2.0 * zx * zy + cY, tmp
i -= 1
pix[x, y] = (i << 21) + (i << 10) + i * 8
bitmap.save("1.png", "PNG")

Mandelbrot集合
iter_func = lambda z, c: (z ** 2 + c)
#迭代公式
def calc_steps(c,max_iter_num = 128):
z = complex(0,0)
num = 0
while abs(z) < 2 and num < max_iter_num:
z = iter_func(z, c)
num = num + 1
return num
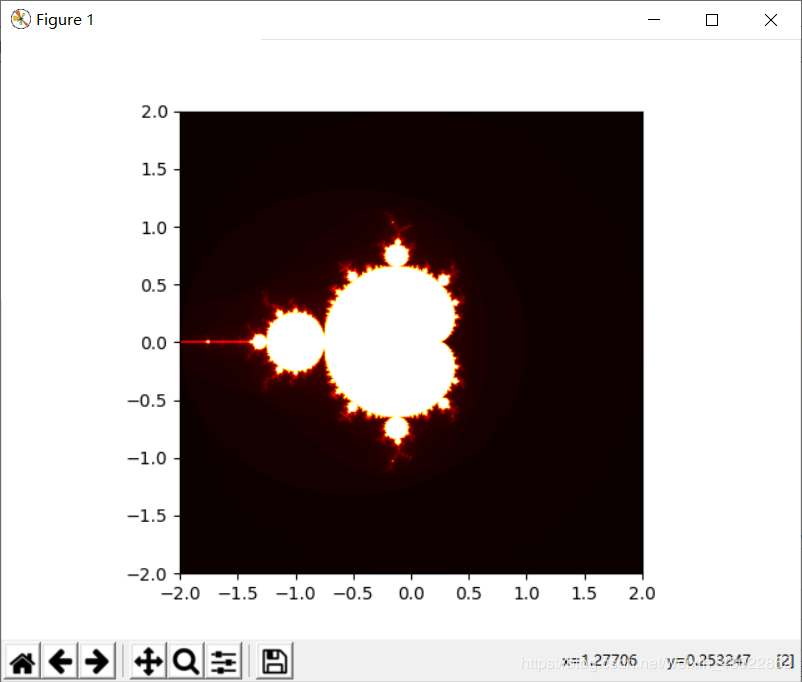
def display_mandelbrot(x_num = 1000, y_num =100):
X,Y = np.meshgrid(np.linspace(-2,2,x_num+1),np.linspace(-2,2,y_num+1))
C = X + Y*1j
result = np.zeros((y_num+1,x_num+1))
#计算出结果
for i in range(y_num+1):
for j in range(x_num+1):
result[i,j] = calc_steps(C[i,j])
plt.imshow(result,interpolation="bilinear",cmap=plt.cm.hot,
vmax=abs(result).max(),vmin=abs(result).min(),
#控制区域在 -2 2的一个矩形里面
extent=[-2,2,-2,2])
plt.show()
Julia集合
iter_func = lambda z, c: (z ** 2 + c)
def calc_steps(z, c,max_iter_num=128):
num = 0
while abs(z) < 2 and num < max_iter_num:
z = iter_func(z, c)
num = num + 1
return num
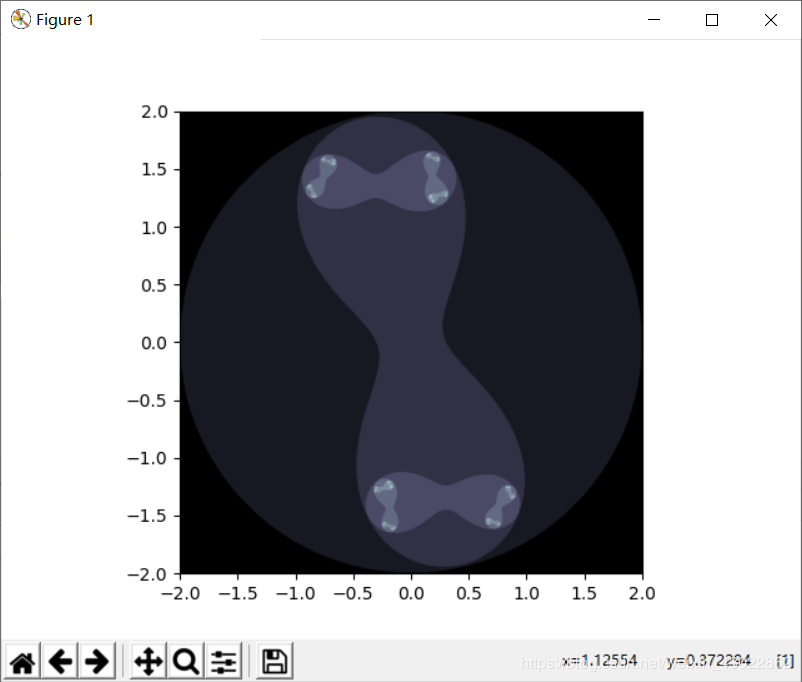
def display_julia(x_num=100, y_num=100):
X, Y = np.meshgrid(np.linspace(-2, 2, x_num + 1), np.linspace(-2, 2, y_num + 1))
C = X + Y * 1j
result = np.zeros((y_num + 1, x_num + 1))
# 计算出结果
c=complex(round(random.uniform(-2, 2),5),round(random.uniform(-2, 2),5))
for i in range(y_num + 1):
for j in range(x_num + 1):
result[i, j] = calc_steps(C[i, j],c)
plt.imshow(result, interpolation="bilinear", cmap=plt.cm.bone ,
vmax=abs(result).max(), vmin=abs(result).min(),
# 控制区域在 -2 2的一个矩形里面
extent=[-2, 2, -2, 2])
plt.show()
上面的代码我借鉴了很多文章和论文,我会在下面给出原文链接