基于城市车辆设备维修遗传算法解全局最优解数据处理

Serepta ·

更新时间:2024-11-13

· 624 次阅读

这个遗传算法解全局最优解主要是解决城市车辆维修费用采用哪种方式维修花费最少。

 以def开头的四个函数是数据处理的主要部分
1 获取方程组的左边部分（矩阵计算）
2 构造方程组右边部分
3 各个参数值求和部分
4 可视化评估最小值部分
 算法函数调用部分

这五个模块就够了（sympy与scipy主要用来解非线性方程组）

import numpy
import scipy
from scipy.optimize import fsolve
import sympy
import matplotlib.pyplot as plt

四个函数处理矩阵
函数1：调取矩阵，生成方程组左边公式

'''将概率矩阵和初始费用矩阵，按照策略矩阵的排序，生成五个方程'''
def get_equation(tactics_dic, transfer_probability, initial_cost_list, x_list, f):
    all_pw_list = []
    for t in range(len(tactics_dic)):
        f = f    #f默认是0.9
        tactics_project = tactics_dic[t]  # 得到其中一个策略矩阵（5个数）   共四个
        pw_list = []
        for r in range(len(tactics_project)):  # 遍历这五个数
            if tactics_project[r] == 1:  # 按照策略矩阵中的数确定初始花费取哪个值
                initial_cost = initial_cost_list[0]   #如果是1，则取50000
                if r == 0:  # 确定概率矩阵的行
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]   #取第一个矩阵的第一个列表的第一个
                        sum_pw = sum_pw + pw     #叠加
                    pw_list.append(initial_cost + f * (sum_pw))   #公式左边生成
                elif r == 1:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 2:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 3:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 4:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
            elif tactics_project[r] == 2:
                initial_cost = initial_cost_list[1]
                if r == 0:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 1:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 2:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 3:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 4:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
            elif tactics_project[r] == 3:
                initial_cost = initial_cost_list[2]
                if r == 0:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 1:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 2:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 3:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 4:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
            elif tactics_project[r] == 4:
                initial_cost = initial_cost_list[3]
                if r == 0:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 1:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 2:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 3:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
                elif r == 4:
                    sum_pw = 0
                    for j in range(len(transfer_probability[t])):
                        pw = x_list[j] * transfer_probability[t][r][j]
                        sum_pw = sum_pw + pw
                    pw_list.append(initial_cost + f * (sum_pw))
        all_pw_list.append(pw_list)
        print('第{}种决策{}数据已处理完毕'.format(t, tactics_project))
    return all_pw_list   #返回所有公式的左边部分，共20个，分四组

函数2：构造方程组右边，并求解方程组的解

'''求解方程组，构造方程组格式'''
def solve_equation(all_tactics_equation):
    all_result=[]
    for tactics_equation in all_tactics_equation:
        tactics_equation_list=tactics_equation
        for equation in tactics_equation_list:
            if tactics_equation_list.index(equation)==0:
                eq_1=equation-x1
            elif tactics_equation_list.index(equation)==1:
                eq_2=equation-x2
            elif tactics_equation_list.index(equation)==2:
                eq_3=equation-x3
            elif tactics_equation_list.index(equation)==3:
                eq_4=equation-x4
            elif tactics_equation_list.index(equation)==4:
                eq_5=equation-x5
        result = sympy.solve([eq_1,eq_2,eq_3,eq_4,eq_5], (x1, x2, x3, x4, x5))
        all_result.append(result)
    return all_result    #返回方程组的解，既个策略下对应的各个参数的值

函数3：将解求和并评估全局最优解，生成可视化散点图

'''将参数值求和，求总值'''
def get_sum(all_result):
    sum_result_list = []
    for result in all_result:
        sum_result=0
        for x in result:
            sum_result=sum_result+result[x]
        sum_result_list.append(sum_result)
    return sum_result_list
'''根据总值将结果可视化，即可清晰看出全局最优解'''
def draw(sum_result_list):
    plt.figure()
    plt.title('Cost comparision under each tactics')
    plt.scatter([1,2,3,4],sum_result_list)
    plt.xlabel('tactics_number')
    plt.ylabel('cost')
    plt.ylim(5000000,5800000)
    plt.savefig(r'C:\Users\liqiyan\Desktop\遗传算法_费用图')
    plt.show()

第二大部分：遗传算子矩阵与概率矩阵的输入，参数的定义

#二  矩阵数据输入部分
#定义变量
x1,x2,x3,x4,x5=sympy.symbols('x1 x2 x3 x4 x5',real=True)
#决策矩阵字典(共24种，这里列出4种）(实列中是：3，15，22，24）
tactics_dic=[(1,1,2,3,3),(1,2,2,3,3),(1,2,3,3,4),(1,2,3,4,4)]
# tactics_dic={'D1':(1,1,2,2,3),'D2':(1,1,2,2,4),'D3':(1,1,2,3,3),'D4':(1,1,2,3,4), \
#              'D5':(1,1,2,4,3),'D6':(1,1,2,4,4),'D7':(1,1,3,2,3),'D8':(1,1,3,2,4), \
#              'D9':(1,1,3,3,3),'D10':(1,1,3,3,4),'D11':(1,1,3,4,3),'D12':(1,1,3,4,4), \
#              'D13':(1,2,2,2,3),'D14':(1,2,2,2,4),'D15':(1,2,2,3,3),'D16':(1,2,2,3,4), \
#              'D17':(1,2,2,4,3),'D18':(1,2,2,4,4),'D19':(1,2,3,2,3),'D20':(1,2,3,2,4), \
#              'D21':(1,2,3,3,3),'D22':(1,2,3,3,4),'D23':(1,2,3,4,3),'D24':(1,2,3,4,4)}
#维修状态转移概率矩阵字典
transfer_probability=[[(0.8,0.2,0,0,0),(0,0.7,0.3,0,0),(0.1,0.2,0.4,0.3,0),(0.7,0.3,0,0,0),(0.6,0.3,0.1,0,0)], \
                      [(0.8,0.2,0,0,0),(0.6,0.3,0.1,0,0),(0.1,0.2,0.4,0.3,0),(0.7,0.3,0,0,0),(0.6,0.3,0.1,0,0)], \
                      [(0.8,0.2,0,0,0),(0.6,0.3,0.1,0,0),(0.8,0.2,0,0,0),(0.7,0.3,0,0,0),(0.6,0.3,0.1,0,0)], \
                      [(0.8,0.2,0,0,0),(0.6,0.3,0.1,0,0),(0.8,0.2,0,0,0),(0.9,0.1,0,0,0),(0.6,0.3,0.1,0,0)]]
# transfer_probability={'P1':(1,1,2,2,3),'P2':(1,1,2,2,4),'P3':[(0.8,0.2,0,0,0),(0,0.7,0.3,0,0),(0.1,0.2,0.4,0.3,0),(0.7,0.3,0,0,0),(0.6,0.3,0.1,0,0)],'P4':(1,1,2,3,4), \
#                      'P5':(1,1,2,4,3),'P6':(1,1,2,4,4),'P7':(1,1,3,2,3),'P8':(1,1,3,2,4), \
#                      'P9':(1,1,3,3,3),'P10':(1,1,3,3,4),'P11':(1,1,3,4,3),'P12':(1,1,3,4,4), \
#                      'P13':(1,2,2,2,3),'P14':(1,2,2,2,4),'P15':(1,2,2,3,3),'P16':(1,2,2,3,4), \
#                      'P17':(1,2,2,4,3),'P18':(1,2,2,4,4),'P19':(1,2,3,2,3),'P20':(1,2,3,2,4), \
#                      'P21':(1,2,3,3,3),'P22':(1,2,3,3,4),'P23':(1,2,3,4,3),'P24':(1,2,3,4,4)}
#初始花费列表
initial_cost_list=[50000,200000,300000,500000]
#参数列表
x_list=[x1,x2,x3,x4,x5]
f=0.9

第三部分：函数调用部分

#三  程序入口，调用算法函数进行处理
if __name__ == '__main__':
    all_tactics_equation=get_equation(tactics_dic, transfer_probability, initial_cost_list, x_list, f)
    all_result=solve_equation(all_tactics_equation)
    sum_result_list=get_sum(all_result)
    draw(sum_result_list)

最终结果：
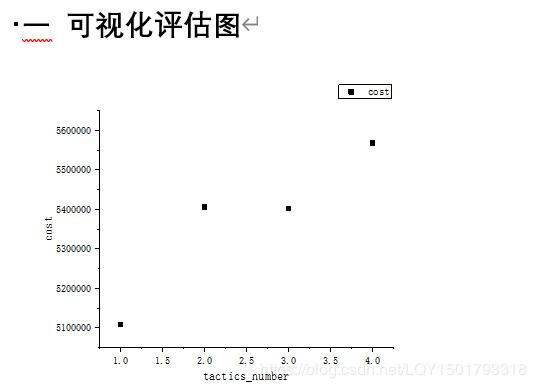
在这里插入图片描述
经过数据处理之后，显然在策略（1，1，2，3，3）中费用最少，为全局最优解。