遗传算法求解高维函数(含MATLAB代码)
文前推广
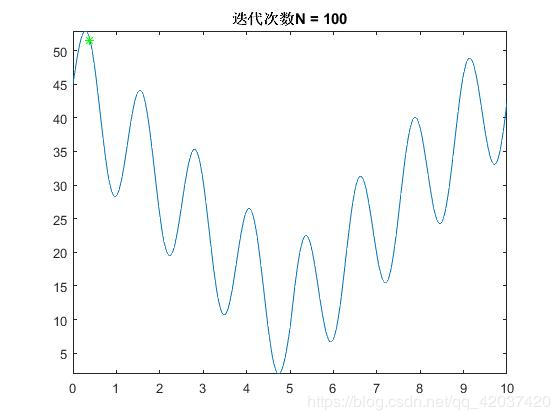
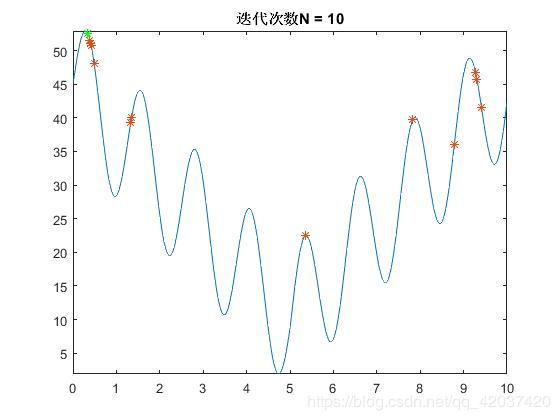 N=100
N=100
 函数1.function pop=initpop(popsize,chromlength)
函数1.function pop=initpop(popsize,chromlength)
作者:猫和真人
《遗传算法求解高维函数》
—— 我上传CSDN的资源是0积分下载,但是系统会自动上调下载量高的资源。所以大家可以使用下方链接,本文所用MATLAB代码已整理至下方链接中。
链接:https://c-t.work/s/73eca467435649 [奶牛快传,打开链接就能下载,无限速、无需注册、无需客户端,一家即用即走的在线分享资源的网站,不想用百度盘的可以试一下!][QQ浏览器进入链接可能会出现“打开异常”或“需要取件码”的情况,只需要更换其他浏览器打开即可]
本文代码出自网络上一位大神,年久失源,若代码原作者申明版权,请联系我进行删除!
高维函数属于NP问题,目前无标准方程可解。
用于求解“非劣解”逼近“最优解”的办法有很多,现在介绍“群智能算法”求解“高维函数”:
【暂时先放MATLAB主程序代码,具体的算法分析会慢慢补充。
【需要MATLAB完整代码的去文章顶部的链接里面拿。
function genetic_algorithm_main()
clear;
clc;
popsize=100;%种群大小
chromlength=10;%(染色体长度)二进制编码长度
pc = 0.6;%交叉概率
pm = 0.001;%变异概率
pop = initpop(popsize,chromlength);%初始化种群
for i = 1:100
%计算适应度值(函数值)
%函数“cal_objvalue里面就存着需要解的高维函数:objvalue=10*sin(5*x)+7*abs(x-5)+10;”
objvalue = cal_objvalue(pop);%得到目标函数值objvalue
fitvalue = objvalue;
newpop = selection(pop,fitvalue);%选择操作
newpop = crossover(newpop,pc);%交叉操作
newpop = mutation(newpop,pm);%变异操作
pop = newpop;%更新种群
%寻找最优解,找到适应度最大的个体->
[bestindividual,bestfit] = best(pop,fitvalue);
x2 = binary2decimal(bestindividual);%最佳个体
y2 = cal_objvalue(bestindividual);%最佳个体目标函数值
x1 = binary2decimal(newpop);%种群
y1 = cal_objvalue(newpop);%种群的目标函数值
if mod(i,10) == 0 %mod函数求i除以10的余数
%if i/10==1 %测试用,测试迭代次数为10时的值
figure;%创建一个图形窗口
%在指定范围内绘制函数图像->
%fplot('10.*sin(5*x)+7.*abs(x-5)+10',[0 10]);
fplot((@(x)10.*sin(5.*x)+7.*abs(x-5)+10),[0 10]);
%数字后加点表示与之相乘的是值而不是向量>%5.2f\n',x2);
fprintf('The best Y is --->>%5.2f\n',bestfit);
遗传算法求解高维函数结果如下:
N=10 N=100
N=100 函数1.function pop=initpop(popsize,chromlength)
函数1.function pop=initpop(popsize,chromlength)
%初始化种群大小
%输入变量:
%popsize:种群大小
%chromlength:染色体长度-->>转化的二进制长度
%输出变量:
%pop:种群
function pop=initpop(popsize,chromlength)
pop = round(rand(popsize,chromlength));
%rand(3,4)生成3行4列的0-1之间的随机数
% rand(3,4),即种群大小为3,染色体二进制长度为4
%
% ans =
%
% 0.8147 0.9134 0.2785 0.9649
% 0.9058 0.6324 0.5469 0.1576
% 0.1270 0.0975 0.9575 0.9706
%round就是四舍五入
% round(rand(3,4))=
% 1 1 0 1
% 1 1 1 0
% 0 0 1 1
%所以返回的种群就是每行是一个个体,列数是染色体长度
函数2.function [objvalue] = cal_objvalue(pop)
%计算函数目标值
%输入变量:二进制数值pop,即种群
%输出变量:目标函数值
function [objvalue] = cal_objvalue(pop)
x = binary2decimal(pop);%函数作用为将二进制转十进制
%转化二进制数为x变量的变化域范围的数值
objvalue=10*sin(5*x)+7*abs(x-5)+10;
函数3.function [newpop] = selection(pop,fitvalue)
%如何选择新的个体
%输入变量:pop二进制种群,fitvalue:适应度值
%输出变量:newpop选择以后的二进制种群
function [newpop] = selection(pop,fitvalue)
%构造轮盘
[px,py] = size(pop);%py没有用到,多余的
totalfit = sum(fitvalue);
p_fitvalue = fitvalue/totalfit;
p_fitvalue = cumsum(p_fitvalue);%概率求和排序
ms = sort(rand(px,1));%从小到大排列
fitin = 1;
newin = 1;
while newin<=px
if(ms(newin))<p_fitvalue(fitin)
newpop(newin,:)=pop(fitin,:);% 若个体的适应值较高,则有很大可能复制自己的数量,其他的劣种就会变少
newin = newin+1;% 一定会选满种群才会跳出循环
else
fitin=fitin+1;
end
end
函数4.function [newpop] = crossover(pop,pc)
%交叉变换
%输入变量:pop:二进制的父代种群数,pc:交叉的概率
%输出变量:newpop:交叉后的种群数
function [newpop] = crossover(pop,pc)
[px,py] = size(pop);
newpop = ones(size(pop));
for i = 1:2:px-1
if(rand<pc)
cpoint = round(rand*py);
newpop(i,:) = [pop(i,1:cpoint),pop(i+1,cpoint+1:py)];
newpop(i+1,:) = [pop(i+1,1:cpoint),pop(i,cpoint+1:py)];
else
newpop(i,:) = pop(i,:);
newpop(i+1,:) = pop(i+1,:);
end
end
函数5.function [newpop] = mutation(pop,pm)
%关于编译
%函数说明
%输入变量:pop:二进制种群,pm:变异概率
%输出变量:newpop变异以后的种群
function [newpop] = mutation(pop,pm)
[px,py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
if(rand<pm)
mpoint = round(rand*py);
if mpoint <= 0
mpoint = 1;
end
newpop(i,:) = pop(i,:);
if newpop(i,mpoint) == 0
newpop(i,mpoint) = 1;
else newpop(i,mpoint) == 1
newpop(i,mpoint) = 0;
end
else newpop(i,:) = pop(i,:);
end
end
函数6.function [bestindividual bestfit] = best(pop,fitvalue)
%求最优适应度函数
%输入变量:pop:种群,fitvalue:种群适应度
%输出变量:bestindividual:最佳个体,bestfit:最佳适应度值
function [bestindividual bestfit] = best(pop,fitvalue)
[px,py] = size(pop);
bestindividual = pop(1,:);%先默认第一个为最佳个体的初值
bestfit = fitvalue(1);%默认第一个为最佳适应度的初值
for i = 2:px %px为行,从每行挨个找
if fitvalue(i)>bestfit %挨个比较适应度的大小
bestindividual = pop(i,:);
bestfit = fitvalue(i);
end
end
函数7.function pop2 = binary2decimal(pop)
%二进制转化成十进制函数
%输入变量:
%二进制种群pop
%输出变量
%十进制数值pop2
function pop2 = binary2decimal(pop)
[px,py]=size(pop);%px为数组pop的行数,py为列数
for i = 1:py%py为染色体长度
pop1(:,i) = 2.^(py-i).*pop(:,i);
end
%sum(.,2)对行求和,得到列向量
temp = sum(pop1,2);
pop2 = temp*10/1023;
关注我的博客,后续还会有详细的算法讲解,有条件的同学多多支持,也可以帮我推广一下哦~
作者:猫和真人
相关文章
Serafina
2021-03-06
Vanessa
2020-12-27
Joy
2020-10-18
Felcia
2020-01-10
Ianthe
2023-07-20
Ursula
2023-07-20
Valora
2023-07-20
Serena
2023-07-20
Edana
2023-07-20
Dabria
2023-07-20
Paula
2023-07-20
Radinka
2023-07-20
Peony
2023-07-20
Rayna
2023-07-20
Fawn
2023-07-21
Tia
2023-07-21
Victoria
2023-07-21
Tertia
2023-07-21
Olathe
2023-07-21