深度学习基础3——过拟合欠拟合、梯度消失与梯度爆炸、常见循环神经网络
深度学习基础3
文章目录深度学习基础3一、过拟合欠拟合1.概念2.解决过拟合欠拟合的方法（1）权重缩减（2）丢弃法二、梯度消失与梯度爆炸1.消失与爆炸2.随机初始化3.影响模型效果的其他因素三、循环神经网络进阶1.门控循环神经网络/门控循环单元(GRU)2.LSTM:长短期记忆3.深度循环神经网络(Deep RNN)4.双向循环神经网络(BRNN)
一、过拟合欠拟合 1.概念 欠拟合：训练误差（训练集的损失函数的值）较大。 过拟合：训练误差远远小于泛化误差（任意测试样本误差的期望）。 验证集：在训练集和测试集中事先留取一部分数据，以便估计泛化误差、确定模型参数超参数、进行模型选择。 K折交叉验证：数据不足以留取验证集时可以采用KKK折交叉验证方法。 其原理是：将原始训练集分割成KKK个不重合的子数据集，对其做K次训练和验证。每次过程用K−1K-1K−1个子集训练模型，用剩余一个子集验证模型。最后求KKK个训练误差和验证误差的均值。 有时一组参数的训练误差可能很低，而在K折交叉验证上的误差较高，这可能是因为存在过拟合。所以，当训练误差降低时，需要观察K折交叉验证上的误差是否相应降低。 影响过拟合和欠拟合的因素有模型复杂度和训练集大小。 训练集样本数过少易出现过拟合的情况。对于模型复杂度，如下图所示，模型较简单时泛化误差和训练误差较高；当模型过于复杂时训练误差降低而泛化误差会升高。因此在选择模型时，模型不能简单也不能过于复杂。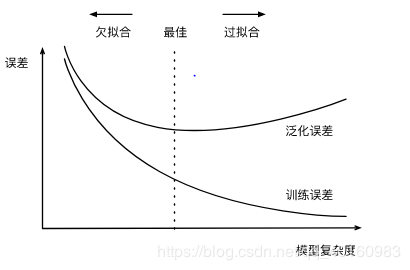
2.解决过拟合欠拟合的方法 （1）权重缩减 权重缩减解决过拟合的方法是通过在损失函数中添加L2L_2L2范数的正则化项（即惩罚项），降低模型参数值。 L2L_2L2范数是权重参数的平方和与一个正数的乘积，如：loss(w,b)+λ∣w∣2loss(\pmb{w},b)+\lambda |\pmb{w}|^2loss(www,b)+λ∣www∣2。 当λ\lambdaλ较大时，惩罚项随之增大，为了使整个损失函数尽可能小，通常会使权重参数w\pmb{w}www压缩到接近于0。 权重缩减通过惩罚绝对值较大的参数为模型增加限制，从而减少过拟合的可能性。
（2）丢弃法 丢弃法—对神经网络的输入层或隐藏层： 随机选择一部分该层的输出作为丢弃元素 将丢弃元素×0 拉伸非丢弃元素 丢弃概率是丢弃法的超参数，丢弃法不改变输入的期望值。在隐藏层使用丢弃法时，由于丢弃的隐藏单元是随机的，所以输出层无法完全依赖所有隐藏单元，从而起到正则化的作用，可以解决过拟合问题。 注：测试模型时一般不使用丢弃法 下图为一个例子：隐藏层原有5个隐藏单元，通过随机选择，丢弃h2,h5h_2,h_5h2,h5，根据剩下三个隐藏单元输出。
二、梯度消失与梯度爆炸 1.消失与爆炸 当神经网络层数较多时，模型的数值稳定性容易变差，易出现的问题是消失和爆炸。 举个例子：假设一个有LLL层的多层感知机的隐藏层的激活函数都是恒等映射（ϕ(x)=x\phi(x)=xϕ(x)=x），即 H(l)=XW(1)…W(l)H^{(l)}=XW^{(1)}…W^{(l)}H(l)=XW(1)…W(l)，从而H(l)H^{(l)}H(l)会消失或爆炸。设权重参数为0.1，如第20层的输出为 0.120X=1×10−20X0.1^{20}X=1×10^{-20}X0.120X=1×10−20X（消失）；如权重参数为2，则第20层的输出为220≈10485762^{20}≈1048576220≈1048576（爆炸）。同时，梯度也会消失会爆炸。 激活函数sigmoid或tanh函数使得参数转换为绝对值小于1的值，会加剧梯度消失的现象。所以在深层网络中需要避免以上两种激活函数
2.随机初始化 随机初始化模型参数的原因：若参数初始值相同，则在正向传播输出值也相同，那么在反向传播中梯度相同，从而更新后值相同，而隐藏单元仅仅一个起作用。 pytorch提供了初始化方法：
3.影响模型效果的其他因素 协变量偏移：特征分布变化，即P(x)P(x)P(x)变化而P(y∣x)P(y|x)P(y∣x)不变 标签偏移：标签边缘分布变化，即P(y)P(y)P(y)变化而P(x∣y)P(x|y)P(x∣y)不变。简单理解为测试中出现了训练时不存在的标签。 概念偏移：标签本身定义发生变化。可以根据其缓慢变化的特点缓解。
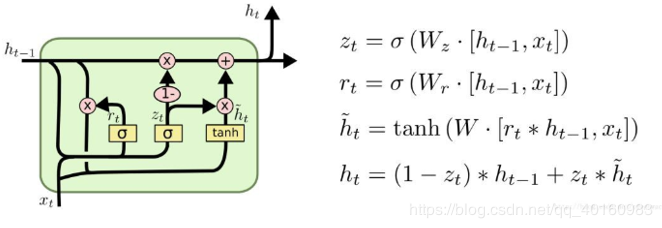表达式为：Rt=σ(Xt+Wxr+Ht−1Whr+br)Zt=σ(Xt+Wxz+Ht−1Whz+bz)H~t=tanh(XtWxh+(Rt⊙Ht−1Whh+bh)Ht=Zt⊙Ht−1+(1−Zt)⊙H~t\begin{aligned}R_t&=\sigma(X_t+W_{xr}+H_{t-1}W_{hr}+b_r)\\Z
_t&=\sigma(X_t+W_{xz}+H_{t-1}W_{hz}+b_z)\\
\tilde{H}_t&=tanh(X_tW_{xh}+(R_{t} \odot H_{t-1}W_{hh}+b_h)\\H
_t&=Z_t \odot H_{t-1}+(1-Z_t)\odot \tilde{H}_{t}
\end{aligned}RtZtH~tHt=σ(Xt+Wxr+Ht−1Whr+br)=σ(Xt+Wxz+Ht−1Whz+bz)=tanh(XtWxh+(Rt⊙Ht−1Whh+bh)=Zt⊙Ht−1+(1−Zt)⊙H~t 其中RtR_tRt为重置门，表示丢弃先前信息的程度。
ZtZ_tZt为更新门，决定丢弃哪些信息和添加哪些新信息。
参考blog：https://www.jianshu.com/p/0cf7436c33ae.
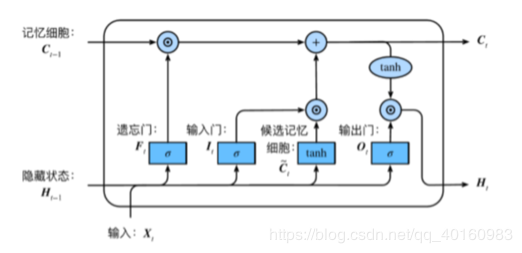
2.LSTM:长短期记忆 LSTM也是为了解决长依赖问题。它的核心思想是记忆细胞，见下图的CtC_tCt。 第一步是决定细胞状态需要丢弃哪些信息—遗忘门FtF_tFt 第二步决定添加哪些新信息----首先由输入门ItI_tIt决定更新哪些信息，然后将 ht−1h_{t-1}ht−1和xtx_txt通过tanhtanhtanh转换后得到一个新的候选记忆细胞C~t\tilde{C}_tC~t，这些信息可能会被更新到细胞信息中 第三步更新旧的细胞信息Ct−1C_{t-1}Ct−1为新的细胞信息CtC_tCt–通过遗忘门遗忘一些旧的信息，通过输出门添加候选细胞信息的一部分 最后一步得到该单元的输出—根据更新的细胞状态判断输出细胞的哪些状态特征并经过tanhtanhtanh转换，与输出门OtO_tOt相乘得到结果
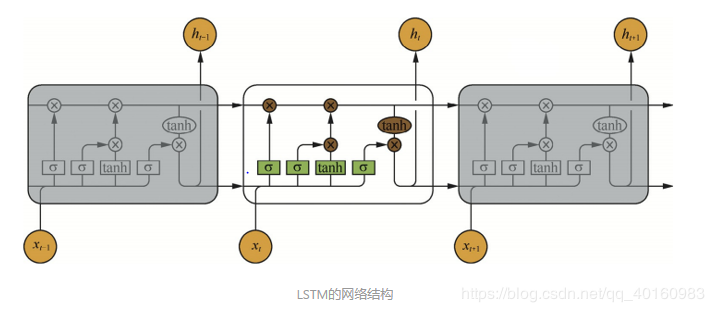表达式：It=σ(XtWxi+Ht−1Whi+bi)Ft=σ(XtWxf+Ht−1Whf+bf)Ot=σ(XtWxf+Ht−1Whf+bf)C~t=tanh(XtWxc+Ht−1Whc+bc)Ct=Ft⊙Ct−1+It⊙C~tHt=Ot⊙tanh(Ct)\begin{aligned}I_t&=\sigma(X_tW_{xi}+H_{t-1}W_{hi}+b_i)\\
F_t&=\sigma(X_tW_{xf}+H_{t-1}W_{hf}+b_f)\\O
_t&=\sigma(X_tW_{xf}+H_{t-1}W_{hf}+b_f)\\
\tilde{C}_t&=tanh(X_tW_{xc}+H_{t-1}W_{hc}+b_c)\\
C_t&=F_t \odot C_{t-1}+I_t \odot \tilde{C}_t\\H_t &=O_t \odot tanh(C_t)
\end{aligned}ItFtOtC~tCtHt=σ(XtWxi+Ht−1Whi+bi)=σ(XtWxf+Ht−1Whf+bf)=σ(XtWxf+Ht−1Whf+bf)=tanh(XtWxc+Ht−1Whc+bc)=Ft⊙Ct−1+It⊙C~t=Ot⊙tanh(Ct)其中FtF_tFt为遗忘门，控制前一步记忆单元中的信息有多大程度被遗忘掉
ItI_tIt为输入门，表示新状态以多大程度更新到记忆单元中
OtO_tOt为输出门，表示当前输出有多大程度取决于当前记忆单元
CtC_tCt为记忆细胞，一种特殊的隐藏状态的信息流动 当输入的序列中没有重要信息时，遗忘门的值接近于1，输入门的值接近于0，此时过去的记忆会被保存，从而实现了长期记忆功能；当输入的序列中出现了重要的信息时，LSTM将其存入记忆中，此时其输入门的值会接近于1；如果该重要信息意味着之前的记忆不再重要时，输入门的值接近1，而遗忘门的值接近于0，这样旧的记忆被遗忘，新的重要信息被记忆。 参考blog：https://www.jianshu.com/p/95d5c461924c. 3.深度循环神经网络(Deep RNN) 深度循环神经网络由多个隐藏层组成，在每个时间上有多个隐藏单元。
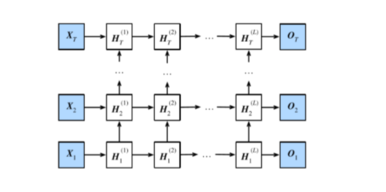表达式：Ht(1)=ϕ(XtWxh(1)+Ht−1(1)Whh(1)+bh(1))⋮Ht(l)=ϕ(Ht(l−1)Wxh(l)+Ht−1(l)Whh(l)+bh(l))Ot=Ht(L)Whh(l)+bq\begin{aligned}H_t^{(1)} &=\phi(X_tW^{(1)}_{xh}+H_{t-1}^{(1)}W_{hh}^{(1)}+b_h^{(1)})\\ & \qquad \qquad \vdots
\\H_t^{(l)} &=\phi(H_t^{(l-1)}W^{(l)}_{xh}+H_{t-1}^{(l)}W_{hh}^{(l)}+b_h^{(l)})\\O_t & =H_t^{(L)}W_{hh}^{(l)}+b_q
\end{aligned}Ht(1)Ht(l)Ot=ϕ(XtWxh(1)+Ht−1(1)Whh(1)+bh(1))⋮=ϕ(Ht(l−1)Wxh(l)+Ht−1(l)Whh(l)+bh(l))=Ht(L)Whh(l)+bq
4.双向循环神经网络(BRNN)
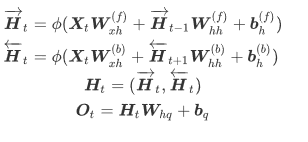
作者：shinning0
一、过拟合欠拟合 1.概念 欠拟合：训练误差（训练集的损失函数的值）较大。 过拟合：训练误差远远小于泛化误差（任意测试样本误差的期望）。 验证集：在训练集和测试集中事先留取一部分数据，以便估计泛化误差、确定模型参数超参数、进行模型选择。 K折交叉验证：数据不足以留取验证集时可以采用KKK折交叉验证方法。 其原理是：将原始训练集分割成KKK个不重合的子数据集，对其做K次训练和验证。每次过程用K−1K-1K−1个子集训练模型，用剩余一个子集验证模型。最后求KKK个训练误差和验证误差的均值。 有时一组参数的训练误差可能很低，而在K折交叉验证上的误差较高，这可能是因为存在过拟合。所以，当训练误差降低时，需要观察K折交叉验证上的误差是否相应降低。 影响过拟合和欠拟合的因素有模型复杂度和训练集大小。 训练集样本数过少易出现过拟合的情况。对于模型复杂度，如下图所示，模型较简单时泛化误差和训练误差较高；当模型过于复杂时训练误差降低而泛化误差会升高。因此在选择模型时，模型不能简单也不能过于复杂。
2.解决过拟合欠拟合的方法 （1）权重缩减 权重缩减解决过拟合的方法是通过在损失函数中添加L2L_2L2范数的正则化项（即惩罚项），降低模型参数值。 L2L_2L2范数是权重参数的平方和与一个正数的乘积，如：loss(w,b)+λ∣w∣2loss(\pmb{w},b)+\lambda |\pmb{w}|^2loss(www,b)+λ∣www∣2。 当λ\lambdaλ较大时，惩罚项随之增大，为了使整个损失函数尽可能小，通常会使权重参数w\pmb{w}www压缩到接近于0。 权重缩减通过惩罚绝对值较大的参数为模型增加限制，从而减少过拟合的可能性。
（2）丢弃法 丢弃法—对神经网络的输入层或隐藏层： 随机选择一部分该层的输出作为丢弃元素 将丢弃元素×0 拉伸非丢弃元素 丢弃概率是丢弃法的超参数，丢弃法不改变输入的期望值。在隐藏层使用丢弃法时，由于丢弃的隐藏单元是随机的，所以输出层无法完全依赖所有隐藏单元，从而起到正则化的作用，可以解决过拟合问题。 注：测试模型时一般不使用丢弃法 下图为一个例子：隐藏层原有5个隐藏单元，通过随机选择，丢弃h2,h5h_2,h_5h2,h5，根据剩下三个隐藏单元输出。
二、梯度消失与梯度爆炸 1.消失与爆炸 当神经网络层数较多时，模型的数值稳定性容易变差，易出现的问题是消失和爆炸。 举个例子：假设一个有LLL层的多层感知机的隐藏层的激活函数都是恒等映射（ϕ(x)=x\phi(x)=xϕ(x)=x），即 H(l)=XW(1)…W(l)H^{(l)}=XW^{(1)}…W^{(l)}H(l)=XW(1)…W(l)，从而H(l)H^{(l)}H(l)会消失或爆炸。设权重参数为0.1，如第20层的输出为 0.120X=1×10−20X0.1^{20}X=1×10^{-20}X0.120X=1×10−20X（消失）；如权重参数为2，则第20层的输出为220≈10485762^{20}≈1048576220≈1048576（爆炸）。同时，梯度也会消失会爆炸。 激活函数sigmoid或tanh函数使得参数转换为绝对值小于1的值，会加剧梯度消失的现象。所以在深层网络中需要避免以上两种激活函数
2.随机初始化 随机初始化模型参数的原因：若参数初始值相同，则在正向传播输出值也相同，那么在反向传播中梯度相同，从而更新后值相同，而隐藏单元仅仅一个起作用。 pytorch提供了初始化方法：
torch.nn.init.normal_()正态分布的随机初始化
Xavier随机初始化：权重参数随机取样于均匀分布U(−6a+b,6a+b)U(-\sqrt{\frac{6}{a+b}},\sqrt{\frac{6}{a+b}})U(−a+b6,a+b6)，aaa为输入个数，bbb为输出个数。3.影响模型效果的其他因素 协变量偏移：特征分布变化，即P(x)P(x)P(x)变化而P(y∣x)P(y|x)P(y∣x)不变 标签偏移：标签边缘分布变化，即P(y)P(y)P(y)变化而P(x∣y)P(x|y)P(x∣y)不变。简单理解为测试中出现了训练时不存在的标签。 概念偏移：标签本身定义发生变化。可以根据其缓慢变化的特点缓解。
表达式为：Rt=σ(Xt+Wxr+Ht−1Whr+br)Zt=σ(Xt+Wxz+Ht−1Whz+bz)H~t=tanh(XtWxh+(Rt⊙Ht−1Whh+bh)Ht=Zt⊙Ht−1+(1−Zt)⊙H~t\begin{aligned}R_t&=\sigma(X_t+W_{xr}+H_{t-1}W_{hr}+b_r)\\Z
_t&=\sigma(X_t+W_{xz}+H_{t-1}W_{hz}+b_z)\\
\tilde{H}_t&=tanh(X_tW_{xh}+(R_{t} \odot H_{t-1}W_{hh}+b_h)\\H
_t&=Z_t \odot H_{t-1}+(1-Z_t)\odot \tilde{H}_{t}
\end{aligned}RtZtH~tHt=σ(Xt+Wxr+Ht−1Whr+br)=σ(Xt+Wxz+Ht−1Whz+bz)=tanh(XtWxh+(Rt⊙Ht−1Whh+bh)=Zt⊙Ht−1+(1−Zt)⊙H~t 其中RtR_tRt为重置门，表示丢弃先前信息的程度。ZtZ_tZt为更新门，决定丢弃哪些信息和添加哪些新信息。
参考blog：https://www.jianshu.com/p/0cf7436c33ae.2.LSTM:长短期记忆 LSTM也是为了解决长依赖问题。它的核心思想是记忆细胞，见下图的CtC_tCt。 第一步是决定细胞状态需要丢弃哪些信息—遗忘门FtF_tFt 第二步决定添加哪些新信息----首先由输入门ItI_tIt决定更新哪些信息，然后将 ht−1h_{t-1}ht−1和xtx_txt通过tanhtanhtanh转换后得到一个新的候选记忆细胞C~t\tilde{C}_tC~t，这些信息可能会被更新到细胞信息中 第三步更新旧的细胞信息Ct−1C_{t-1}Ct−1为新的细胞信息CtC_tCt–通过遗忘门遗忘一些旧的信息，通过输出门添加候选细胞信息的一部分 最后一步得到该单元的输出—根据更新的细胞状态判断输出细胞的哪些状态特征并经过tanhtanhtanh转换，与输出门OtO_tOt相乘得到结果
表达式：It=σ(XtWxi+Ht−1Whi+bi)Ft=σ(XtWxf+Ht−1Whf+bf)Ot=σ(XtWxf+Ht−1Whf+bf)C~t=tanh(XtWxc+Ht−1Whc+bc)Ct=Ft⊙Ct−1+It⊙C~tHt=Ot⊙tanh(Ct)\begin{aligned}I_t&=\sigma(X_tW_{xi}+H_{t-1}W_{hi}+b_i)\\
F_t&=\sigma(X_tW_{xf}+H_{t-1}W_{hf}+b_f)\\O
_t&=\sigma(X_tW_{xf}+H_{t-1}W_{hf}+b_f)\\
\tilde{C}_t&=tanh(X_tW_{xc}+H_{t-1}W_{hc}+b_c)\\
C_t&=F_t \odot C_{t-1}+I_t \odot \tilde{C}_t\\H_t &=O_t \odot tanh(C_t)
\end{aligned}ItFtOtC~tCtHt=σ(XtWxi+Ht−1Whi+bi)=σ(XtWxf+Ht−1Whf+bf)=σ(XtWxf+Ht−1Whf+bf)=tanh(XtWxc+Ht−1Whc+bc)=Ft⊙Ct−1+It⊙C~t=Ot⊙tanh(Ct)其中FtF_tFt为遗忘门，控制前一步记忆单元中的信息有多大程度被遗忘掉ItI_tIt为输入门，表示新状态以多大程度更新到记忆单元中
OtO_tOt为输出门，表示当前输出有多大程度取决于当前记忆单元
CtC_tCt为记忆细胞，一种特殊的隐藏状态的信息流动 当输入的序列中没有重要信息时，遗忘门的值接近于1，输入门的值接近于0，此时过去的记忆会被保存，从而实现了长期记忆功能；当输入的序列中出现了重要的信息时，LSTM将其存入记忆中，此时其输入门的值会接近于1；如果该重要信息意味着之前的记忆不再重要时，输入门的值接近1，而遗忘门的值接近于0，这样旧的记忆被遗忘，新的重要信息被记忆。 参考blog：https://www.jianshu.com/p/95d5c461924c. 3.深度循环神经网络(Deep RNN) 深度循环神经网络由多个隐藏层组成，在每个时间上有多个隐藏单元。
表达式：Ht(1)=ϕ(XtWxh(1)+Ht−1(1)Whh(1)+bh(1))⋮Ht(l)=ϕ(Ht(l−1)Wxh(l)+Ht−1(l)Whh(l)+bh(l))Ot=Ht(L)Whh(l)+bq\begin{aligned}H_t^{(1)} &=\phi(X_tW^{(1)}_{xh}+H_{t-1}^{(1)}W_{hh}^{(1)}+b_h^{(1)})\\ & \qquad \qquad \vdots
\\H_t^{(l)} &=\phi(H_t^{(l-1)}W^{(l)}_{xh}+H_{t-1}^{(l)}W_{hh}^{(l)}+b_h^{(l)})\\O_t & =H_t^{(L)}W_{hh}^{(l)}+b_q
\end{aligned}Ht(1)Ht(l)Ot=ϕ(XtWxh(1)+Ht−1(1)Whh(1)+bh(1))⋮=ϕ(Ht(l−1)Wxh(l)+Ht−1(l)Whh(l)+bh(l))=Ht(L)Whh(l)+bq
4.双向循环神经网络(BRNN)
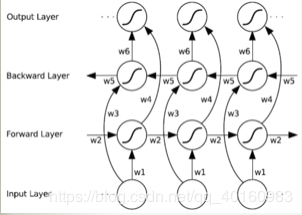
一般的RNN在某一时刻只能从过去的序列和当前输入获取信息，不能从后面序列捕获信息。而BRNN可以。如图所示，向前向后层连接着输出层，包含6个共享权值，分别为：输入到向前向后层的两个权值，向前向后到隐藏层的权重和向前向后隐藏层到输出层的权值。所以，每个训练序列向前向后分别是两个循环网络，连接着一个输出层。这个结构提供给输出层输入序列中每一个点的完整的过去和未来的上下文信息。
表达式：
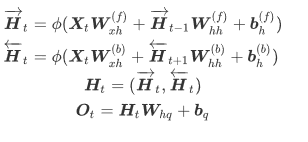
训练过程
参考blog：https://blog.csdn.net/wangyangzhizhou/article/details/79798087
作者：shinning0
