过拟合欠拟合及其解决方案；梯度消失梯度爆炸；循环神经网络进阶；机器翻译及相关技术；注意力机制与Seq2seq模型；Transformer；卷积神经网络基础；leNet；卷积神经网络进阶

Camille ·

更新时间:2024-11-11

· 563 次阅读

1.过拟合欠拟合及其解决方案
一类是模型无法得到较低的训练误差，我们将这一现象称作欠拟合（underfitting）。
模型的训练误差远小于它在测试数据集上的误差，我们称该现象为过拟合（overfitting）。在实践中，我们要尽可能同时应对欠拟合和过拟合。
2.梯度消失梯度爆炸
深度模型有关数值稳定性的典型问题是消失（vanishing）和爆炸（explosion）。
假设一个层数为LLL的多层感知机的第lll层H(l)\boldsymbol{H}^{(l)}H(l)的权重参数为W(l)\boldsymbol{W}^{(l)}W(l)，输出层H(L)\boldsymbol{H}^{(L)}H(L)的权重参数为W(L)\boldsymbol{W}^{(L)}W(L)。为了便于讨论，不考虑偏差参数，且设所有隐藏层的激活函数为恒等映射（identity mapping）ϕ(x)=x\phi(x) = xϕ(x)=x。给定输入X\boldsymbol{X}X，多层感知机的第lll层的输出H(l)=XW(1)W(2)…W(l)\boldsymbol{H}^{(l)} = \boldsymbol{X} \boldsymbol{W}^{(1)} \boldsymbol{W}^{(2)} \ldots \boldsymbol{W}^{(l)}H(l)=XW(1)W(2)…W(l)。此时，如果层数lll较大，H(l)\boldsymbol{H}^{(l)}H(l)的计算可能会出现衰减或爆炸。举个例子，假设输入和所有层的权重参数都是标量，如权重参数为0.2和5，多层感知机的第30层输出为输入X\boldsymbol{X}X分别与0.230≈1×10−210.2^{30} \approx 1 \times 10^{-21}0.230≈1×10−21（消失）和530≈9×10205^{30} \approx 9 \times 10^{20}530≈9×1020（爆炸）的乘积。当层数较多时，梯度的计算也容易出现消失或爆炸。
3.机器翻译及相关技术
机器翻译（MT）：将一段文本从一种语言自动翻译为另一种语言，用神经网络解决这个问题通常称为神经机器翻译（NMT）。
主要特征：输出是单词序列而不是单个单词。输出序列的长度可能与源序列的长度不同。
4.注意力机制与Seq2seq模型
在“编码器—解码器（seq2seq）”⼀节⾥，解码器在各个时间步依赖相同的背景变量（context vector）来获取输⼊序列信息。当编码器为循环神经⽹络时，背景变量来⾃它最终时间步的隐藏状态。将源序列输入信息以循环单位状态编码，然后将其传递给解码器以生成目标序列。然而这种结构存在着问题，尤其是RNN机制实际中存在长程梯度消失的问题，对于较长的句子，我们很难寄希望于将输入的序列转化为定长的向量而保存所有的有效信息，所以随着所需翻译句子的长度的增加，这种结构的效果会显著下降。
与此同时，解码的目标词语可能只与原输入的部分词语有关，而并不是与所有的输入有关。例如，当把“Hello world”翻译成“Bonjour le monde”时，“Hello”映射成“Bonjour”，“world”映射成“monde”。在seq2seq模型中，解码器只能隐式地从编码器的最终状态中选择相应的信息。然而，注意力机制可以将这种选择过程显式地建模。
5.卷积神经网络基础
主要是卷积层和池化层，并解释填充、步幅、输入通道和输出通道的含义。
二维互相关运算

二维互相关（cross-correlation）运算的输入是一个二维输入数组和一个二维核（kernel）数组，输出也是一个二维数组，其中核数组通常称为卷积核或过滤器（filter）。卷积核的尺寸通常小于输入数组，卷积核在输入数组上滑动，在每个位置上，卷积核与该位置处的输入子数组按元素相乘并求和，得到输出数组中相应位置的元素。图1展示了一个互相关运算的例子，阴影部分分别是输入的第一个计算区域、核数组以及对应的输出。
6.leNet

使用全连接层的局限性：

图像在同一列邻近的像素在这个向量中可能相距较远。它们构成的模式可能难以被模型识别。对于大尺寸的输入图像，使用全连接层容易导致模型过大。

使用卷积层的优势：

卷积层保留输入形状。卷积层通过滑动窗口将同一卷积核与不同位置的输入重复计算，从而避免参数尺寸过大。 LeNet 模型

LeNet分为卷积层块和全连接层块两个部分。下面我们分别介绍这两个模块。

Image Name

卷积层块里的基本单位是卷积层后接平均池化层：卷积层用来识别图像里的空间模式，如线条和物体局部，之后的平均池化层则用来降低卷积层对位置的敏感性。

卷积层块由两个这样的基本单位重复堆叠构成。在卷积层块中，每个卷积层都使用5×55 \times 55×5的窗口，并在输出上使用sigmoid激活函数。第一个卷积层输出通道数为6，第二个卷积层输出通道数则增加到16。

全连接层块含3个全连接层。它们的输出个数分别是120、84和10，其中10为输出的类别个数。
7.卷积神经网络进阶
LeNet: 在大的真实数据集上的表现并不尽如⼈意。
1.神经网络计算复杂。
2.还没有⼤量深⼊研究参数初始化和⾮凸优化算法等诸多领域。

机器学习的特征提取:手工定义的特征提取函数
神经网络的特征提取：通过学习得到数据的多级表征，并逐级表⽰越来越抽象的概念或模式。

神经网络发展的限制:数据、硬件
AlexNet
首次证明了学习到的特征可以超越⼿⼯设计的特征，从而⼀举打破计算机视觉研究的前状。
特征：

8层变换，其中有5层卷积和2层全连接隐藏层，以及1个全连接输出层。

将sigmoid激活函数改成了更加简单的ReLU激活函数。

用Dropout来控制全连接层的模型复杂度。

引入数据增强，如翻转、裁剪和颜色变化，从而进一步扩大数据集来缓解过拟合。

 VGG：通过重复使⽤简单的基础块来构建深度模型。

Block:数个相同的填充为1、窗口形状为3×33\times 33×3的卷积层,接上一个步幅为2、窗口形状为2×22\times 22×2的最大池化层。
卷积层保持输入的高和宽不变，而池化层则对其减半。

Image Name

8.Transformer
为了整合CNN和RNN的优势，[Vaswani et al., 2017] 创新性地使用注意力机制设计了Transformer模型。该模型利用attention机制实现了并行化捕捉序列依赖，并且同时处理序列的每个位置的tokens，上述优势使得Transformer模型在性能优异的同时大大减少了训练时间。

图10.3.1展示了Transformer模型的架构，与9.7节的seq2seq模型相似，Transformer同样基于编码器-解码器架构，其区别主要在于以下三点：

Transformer blocks：将seq2seq模型重的循环网络替换为了Transformer Blocks，该模块包含一个多头注意力层（Multi-head Attention Layers）以及两个position-wise feed-forward networks（FFN）。对于解码器来说，另一个多头注意力层被用于接受编码器的隐藏状态。 Add and norm：多头注意力层和前馈网络的输出被送到两个“add and norm”层进行处理，该层包含残差结构以及层归一化。 Position encoding：由于自注意力层并没有区分元素的顺序，所以一个位置编码层被用于向序列元素里添加位置信息。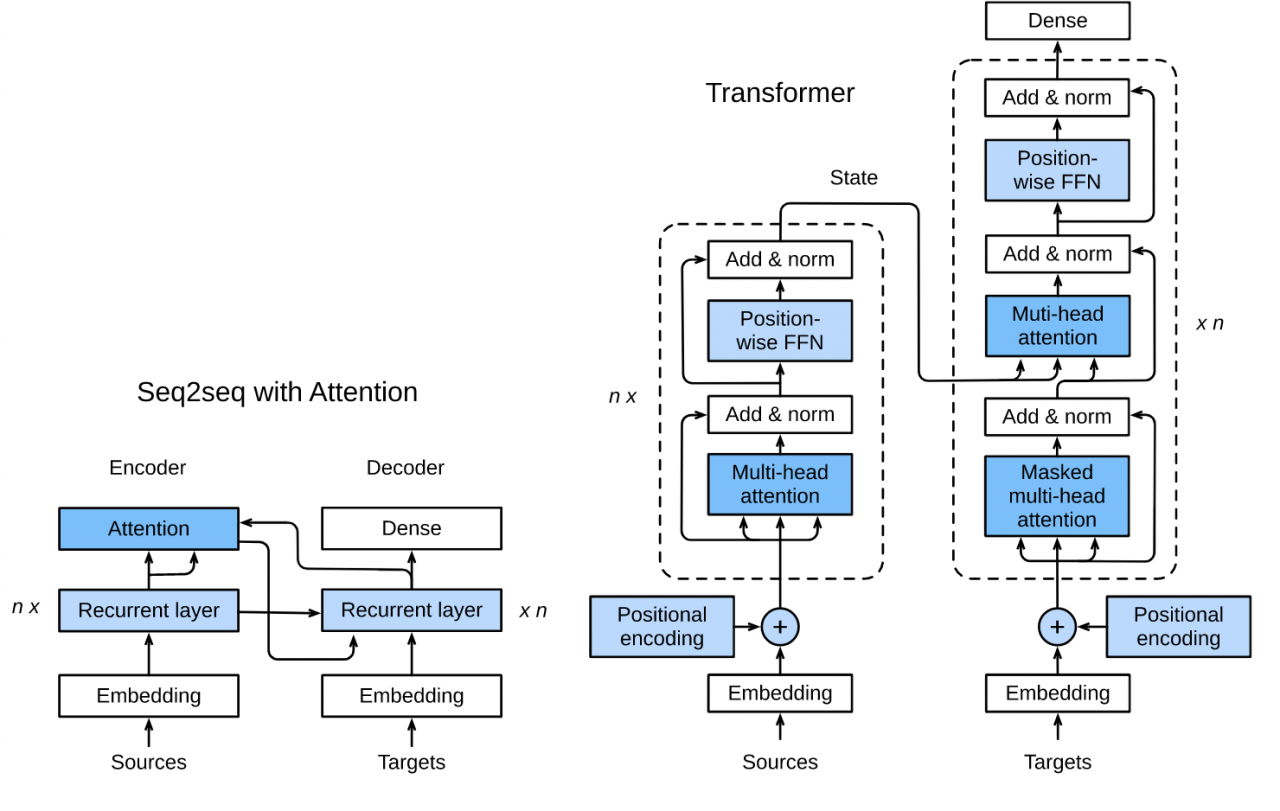

Fig. 10.3.1 The Transformer architecture.