读注释,敲代码,学习数据结构——循环队列
小萌新今天和大家聊聊什么是循环队列,话不多说,开门见山吧!
如果说可以用循环队列解决队列的虚假满的状态,那么什么是虚假满状态?
假设当前顺序队列分配的最大空间是6,当队尾指针从5下标指向6下标时(6下标实际不存在),说明此时队列已满,然而依然可以进行出队的操作,顺序队不能像顺序栈那样进行存储再分配扩大数组空间,所以队列的实际可用空间并未占满。
循环队列就是将顺序队列构造成为一个环状的队列空间,如图:
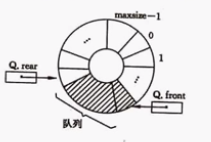
注意:
此时当指针front=指针rear时,无法判断队列空间是满还是空,有两种解决思路:
1.另设一个标志位区分队列空间是满还是空;
2.少用一个空间,约定以“队列头指针在队列尾指针的下一位置”作为队列满的状态标志。
来吧!举个栗子吧,如图:
【情况1】
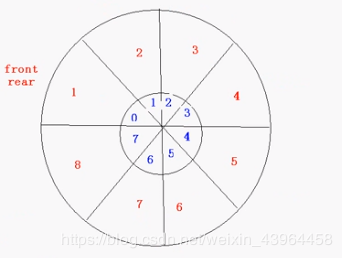
初始化,队头指针front,队尾指针rear都指向0下标;
当存入数据元素1后,队尾指针rear从0下标指向1下标;
当存入数据元素2后,队尾指针rear从1下标指向2下标;
当存入数据元素3后,队尾指针rear从2下标指向3下标;
当存入数据元素4后,队尾指针rear从3下标指向4下标;
…
当存入数据元素8后,队尾指针rear从7下标指向0下标;(队列已满)
如何判断队头指针front与队尾指针rear重合时,队列是空还是满呢?我们假如用flag来标记队头指针front与队尾指针rear的重合状态,于是规定当flag=0时:队列为空;当flag=1时,队列为满。
【情况2】
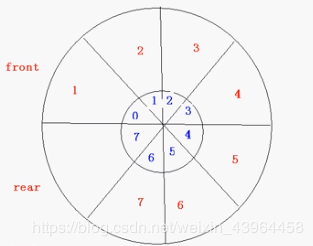
我们把7下标的空间空出不存放数据,当数据元素7进为6下标的空间后,队尾指针rear就指向了为7下标的空间(此时7下标空间是空的),理论上8个空间只用了7个空间,但在逻辑上我们规定此时队列已满。当rear+1后,队头指针front与队尾指针rear重合,说明此时队列空间逻辑已满,我们先将队头指针所指空间的元素出队,队头指针前移指向1下标,此时再将元素进下标为7的空间,队尾指针rear前移(指向0下标),当rear+1后,队头指针front与队尾指针rear又重合,说明此时队列空间逻辑又已满,依次循环往复,出队—>队头指针front前移——>后面入队——>队尾指针rear前移(判断条件是rear+1后,队头指针front与队尾指针rear是否重合,不重合则可继续入队)。
但是,计算机是没有环状的存储空间的,依然是以线性存储的方式,那计算机如何判断什么时候队尾指针再次与队头指针重合呢?
—————OK!那就是:进行模运算—————
具体模运算是怎么实现的,文字显得苍白无力,还是那句话,把代码跑起来,慢慢体会!
#include
#include
#include
#define MAXSIZE 8//定义队列初始化存放8个数据元素
typedef int ElmeType;
/*给出顺序队列的结构*/
typedef struct Queue
{
ElmeType *base;//指针base指向有效的队列空间
int front;//队头指针
int rear;//队尾指针指向下一个有效的空间
}Queue;
/*初始化顺序队列*/
void InitQueue(Queue *Q)
{
Q->base=(ElmeType *)malloc(sizeof(ElmeType)*MAXSIZE);//开辟队列空间
assert(Q->base!=NULL);//断言——是否开辟空间成功
Q->front=Q->rear=0;//队头指针和队尾指针都指向队列的0下标,此时队列为空
}
/*入队*/
void EnQueue(Queue *Q,ElmeType x)
{
//数据入队后,队尾指针从当前空间指向下一个有效的空间,此时称队尾指针是伪指针;
//当伪指针所指下标+1后正好等于队列空间容量时,此时我们希望伪指针可以重新指向队头,而不是出界,于是进行模运算;
//(Q->rear+1)%MAXSIZE——若模为0,则伪指针恰好指向队列的最后一个有效空间,我们需要让此时的伪指针重新指向0下标而不是最后一个有效空间;
//(始终都要将队列最后一个有效空间空出)循环开始:
if((Q->rear+1)%MAXSIZE==Q->front)//若伪指针所指下标+1与队头指针指向相同的下标,此时判断为队列逻辑已满
return;//返回,理论上队列保留了队列最后一个有效空间
Q->base[Q->rear]=x;//否则队列逻辑不满,继续在队尾指针所指下标进行入队,入队完成后,队尾指针又从当前空间指向下一个有效的空间
Q->rear=(Q->rear+1)%MAXSIZE;//当逻辑空间满后,模运算实现队尾指针重新指向0下标而不是最后一个有效空间;
}
/*展示顺序队列元素*/
void ShowQueue(Queue *Q)
{
printf("顺序队列中存放的元素:");
for(int i=Q->front;i!=Q->rear;)
{
printf("%d ",Q->base[i]);//依次打印队头指针所指下标中的数据到队尾指针所指下标中的数据
i=(i+1)%MAXSIZE;//循环打印,7下标不能打印,重新回到0下标(循环时,队尾下标-队头下标=-1)
}
printf("\n");
}
/*出队*/
void DeQueue(Queue *Q)
{
//出队一个元素,队头指针指向下一个有效的数据元素
if(Q->front==Q->rear)//队头队尾指向相同,队列为空
return;
Q->front=(Q->front+1)%MAXSIZE;//队头指针循环,模运算实现队头指针重新指向0下标而不是最后一个有效空间;
}
/*取队头元素*/
void GetHead(Queue *Q,ElmeType *v)//指针v带回队头元素
{
//要获取队头,前提是队列不空
if(Q->front==Q->rear)//队列为空
return;
*v=Q->base[Q->front];//必须在base所指的空间里取元素
}
/*顺序队列的长度*/
int Length(Queue *Q)
{
return (Q->rear - Q->front);
//下标0开始存放数据,进队后,队尾指针指向下一个有效的新空间
//队列中元素的个数正好是队尾队头所指的下标之差
//但是当队列逻辑空间满后,再存储数据需要先出队,再进行入队,此时队尾队头所指的下标之差为-1
}
/*清除顺序队列*/
void ClearQueue(Queue *Q)
{
Q->front=Q->rear=0;//队列置为空
}
/*销毁顺序队列*/
void DestroyQueue(Queue *Q)
{
free(Q->base);//释放base所指的队列空间
Q->base=NULL;//预防野指针
}
/**/
void main()
{
Queue Q;
ElmeType e;//定义队头元素
InitQueue(&Q);//&Q是传入队列的地址
printf("将1,2,3,4,5,6,7,8依次入队\n");
for(int i=1;i<=8;++i)
{
EnQueue(&Q,i);
}
ShowQueue(&Q);
printf("顺序队的长度为:%d\n",Length(&Q));
printf("\n");
printf("进行出队\n");
DeQueue(&Q);
ShowQueue(&Q);
GetHead(&Q,&e);
printf("队头元素为:%d\n",e);
printf("\n");
printf("将元素10入队\n");
EnQueue(&Q,10);
ShowQueue(&Q);
printf("\n");
printf("进行出队\n");
DeQueue(&Q);
ShowQueue(&Q);
GetHead(&Q,&e);
printf("队头元素为:%d\n",e);
printf("\n");
printf("将元素20入队\n");
EnQueue(&Q,20);
ShowQueue(&Q);
printf("\n");
ClearQueue(&Q);
DestroyQueue(&Q);
}
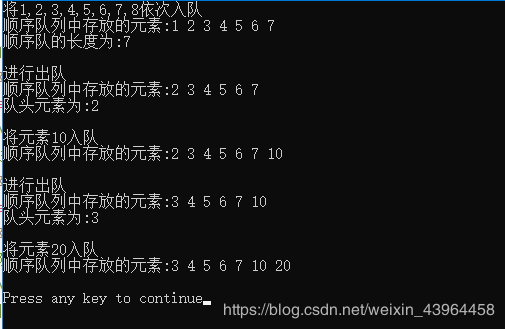
运行结果:
作者:@AS_constancy