密码技术学习笔记（1）——比特序列密码

计算机的操作对象并不是文字，而是由 0 和1排列而成的比特序列。无论是文字 、 图像 、 声音 、 视频还是程序，在计算机中都是用比特序列来表示的。将现实世界中的东西映射为比特序列的操作称为编码 (encoding ) 。

而执行加密操作的程序，就是将表示明文的比特序列转换为表示密文的比特序列。

XOR 的全称是 exclusive or ，在中文里叫作异或。

1 XOR 运算（1 个比特）

1 个比特的 XOR 运算规则如下：

0 XOR 0 = 0 0 XOR 1 = 1 1 XOR 0 = 1 1 XOR 1 = 0

如果将 0 理解为偶数，将1理解为奇数，就可以将 XOR 和一般的加法运算等同起来。

0（偶数） + 0（偶数） = 0（偶数） 0（偶数） + 1（奇数） = 1（奇数） 1（奇数） + 0（偶数） = 1（奇数） 1（奇数） + 1（奇数） = 0（偶数）

由于 XOR 和加法运算很相似，因此一般用符号 ⊕ 来表示 XOR 。

0 ⊕ 0 = 0 0 ⊕ 1 = 1 1 ⊕ 0 = 1 1 ⊕ 1 = 0 2 XOR 运算（比特序列）

如果是长比特序列之间的 XOR 运算，则只要对其中每个相对应的比特进行 XOR 运算就可以了。假设长比特序列 A 为 10100，长比特序列 B 为 10011，那么 A ⊕ B 的运算过程为：

和加法运算不同的是， XOR 中不需要进位。

由于两个相同的数进行 XOR 运算的结果一定为 0 ，因此如果将 A⊕ B 的结果再与 B 进行XOR 运算，则结果会变回 A 。 也就是说，两个算式中的 B 会相互抵消 ，即 （A ⊕ B）⊕ B = A 。

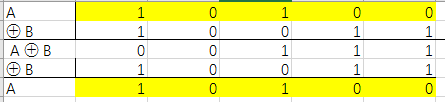
上面的计算过程和加密 、 解密的过程非常相似。

加密：将明文 A 用密钥 B 进行加密，得到密文 A ⊕ B； 解密：将密文 A ⊕ B 用密钥 B 进行解密，得到明文 A。

实际上，只要选择一个合适的 B ，仅仅使用 XOR 就可以实现出一个高强度的密码。

作者：deniro_li

学习笔记 学习 比特