过拟合和欠拟合学习笔记
欠拟合
作者:zy[??]
模型无法得到较低的训练误差(模型在训练数据集上表现出的误差),这一现象称作欠拟合(underfitting)
过拟合过拟合得问题指的是模型在测试集上的结果不好,训练误差较低但是泛化误差依然较高,二者相差较大。
解决过拟合得问题通常可以通过增加数据量,另外还可以用正则化的方法。
通常指得是L2范数正则化,是在损失函数中再加一个正则项λ2n\frac{λ}{2n}2nλ,其中超参数λ>0λ>0λ>0,损失函数如下
J(W,b)+λ2n∣w∣2J(W,b)+\frac{λ}{2n}|w|^2J(W,b)+2nλ∣w∣2,
L2范数表示向量元素的平方和再开平方。
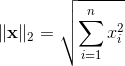
正则化项为λ/2m乘以w范数的平方
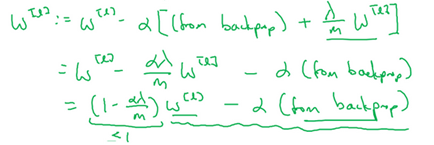
L2 范数正则化令权重 w 先自乘小于1(1-λa/m)的数,再减去不含惩罚项的梯度。因此, L2 范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制,这可能对过拟合有效。
L2正则化可以减少过拟合得原因:
只要参数λ足够的大,权重W的值就可以非常小,甚至接近0 ,使得网络中大量得隐藏单元得影响变小了,从而使得神经网络变得简单了,这样更加不容易发生过拟合。
dropout方法会遍历网络的每一层,设置消除神经网络中节点的概率ppp,设置好之后,该层的隐藏单元将有概率ppp被丢弃掉,这样会消除一些节点,然后删除掉从该节点进出的连线,最后得到一个节点更少,规模更小得网络,从而简化了模型,减少了过拟合的问题。如下图中h4h_4h4和h5h_5h5两个神经元被舍弃了。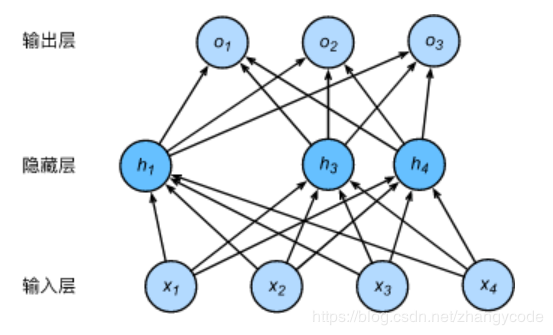
作者:zy[??]