【信号与系统】系统复频域小测验

Author：AXYZdong
自动化专业 工科男
有一点思考，有一点想法，有一点理性！
CSDN@AXYZdong

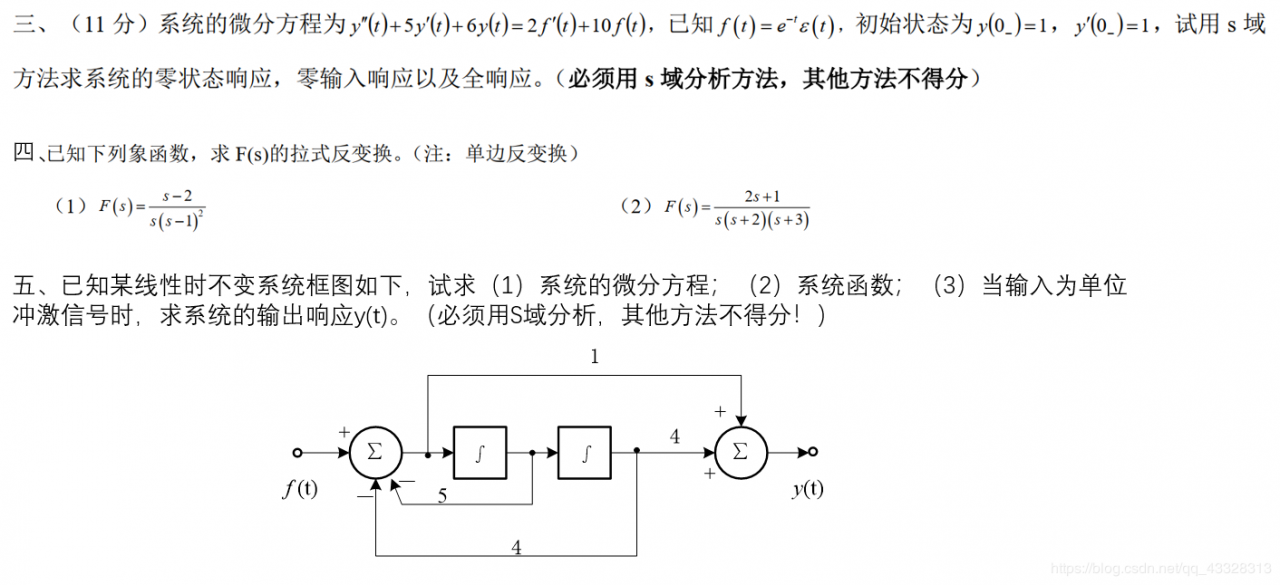
解：微分方程两边取拉氏变换，可得：

(s2+5s+6)Y(s)−sy(0−)−y′(0−)−5y(0−)=(2s+10)F(s)(s^2+5s+6)Y(s)-sy(0_{-})-y'(0_{-})-5y(0_{-})=(2s+10)F(s)(s2+5s+6)Y(s)−sy(0−​)−y′(0−​)−5y(0−​)=(2s+10)F(s)
整理：

Y(s)=s+6s2+5s+6+2s+10s2+5s+6⋅F(s)Y(s)=\frac{s+6}{s^2+5s+6}+\frac{2s+10}{s^2+5s+6}\cdot F(s)Y(s)=s2+5s+6s+6​+s2+5s+62s+10​⋅F(s)

故：YX(s)=s+6s2+5s+6=4s+2+−3s+3,Yf(s)=2s+10s2+5s+6=−6s+2+2s+3+4s+1Y_X(s)=\frac{s+6}{s^2+5s+6}=\frac{4}{s+2}+\frac{-3}{s+3},Y_f(s)=\frac{2s+10} {s^2+5s+6}=\frac{-6}{s+2}+\frac{2}{s+3}+\frac{4}{s+1}YX​(s)=s2+5s+6s+6​=s+24​+s+3−3​,Yf​(s)=s2+5s+62s+10​=s+2−6​+s+32​+s+14​

零状态响应：yf(t)=(2e−3t+4e−t−6e−2t)ϵ(t)y_f(t)=(2e^{-3t}+4e^{-t}-6e^{-2t})\epsilon(t)yf​(t)=(2e−3t+4e−t−6e−2t)ϵ(t)

零输入响应：yX(t)=(4e−2t−3e−3t)ϵ(t)y_X(t)=( 4e^{-2t}-3e^{-3t})\epsilon(t)yX​(t)=(4e−2t−3e−3t)ϵ(t)

全响应：y(t)=(−e−3t+4e−t−2e−2t)ϵ(t)y(t)=(-e^{-3t}+4e^{-t}-2e^{-2t})\epsilon(t)y(t)=(−e−3t+4e−t−2e−2t)ϵ(t)

（1）F(s)=s−2s(s−1)2F(s)=\frac{s-2}{s(s-1)^2}F(s)=s(s−1)2s−2​
解：令：F(s)=k11(s−1)2+k12(s−1)+k2sF(s)=\frac{k_{11}}{(s-1)^2}+\frac{k_{12}}{(s-1) }+\frac{k_2}{s}F(s)=(s−1)2k11​​+(s−1)k12​​+sk2​​

令：F1(s)=(s−1)2F(s)=s−2sF_1(s)=(s-1)^2F(s)=\frac{s-2}{s}F1​(s)=(s−1)2F(s)=ss−2​

k11=F1(s)∣s=1=−1,k12=ddsF1(s)=s−(s−2)s2∣s=1=2,k2=sF(s)∣s=0=−2k_{11}=F_1(s)|_{s=1}=-1,k_{12}=\frac{d}{ds}F_1(s)=\frac{s-(s-2)}{s^2}|_{s=1}=2,k_2=sF(s)|_{s=0}=-2k11​=F1​(s)∣s=1​=−1,k12​=dsd​F1​(s)=s2s−(s−2)​∣s=1​=2,k2​=sF(s)∣s=0​=−2

故：F(s)=−1(s−1)2+2(s−1)+−2sF(s)=\frac{-1}{(s-1)^2}+\frac{2}{(s-1) }+\frac{-2}{s}F(s)=(s−1)2−1​+(s−1)2​+s−2​

F(s)F(s)F(s) 拉式反变换为 f(t)=(−tet+2et−2)ϵ(t)f(t)=(-te^t+2e^t-2)\epsilon(t)f(t)=(−tet+2et−2)ϵ(t)

（2）F(s)=2s+1s(s+2)(s+3)F(s)=\frac{2s+1}{s(s+2)(s+3)}F(s)=s(s+2)(s+3)2s+1​
解：令：F(s)=k1s+k2s+2+k3s+3F(s)=\frac{k_1}{s}+\frac{k_2}{s+2}+\frac{k_3}{s+3}F(s)=sk1​​+s+2k2​​+s+3k3​​
k1=sF(s)∣s=0=1/6,k2=(s+2)F(s)∣s=−2=3/2,k3=(s+3F(s)∣s=−3=−5/3k_1=sF(s)|_{s=0}=1/6,k_2=(s+2)F(s)|_{s=-2}=3/2,k_3=(s+3F(s)|_{s=-3}=-5/3k1​=sF(s)∣s=0​=1/6,k2​=(s+2)F(s)∣s=−2​=3/2,k3​=(s+3F(s)∣s=−3​=−5/3

故：F(s)=16s+32(s+2)+−53(s+3)F(s)=\frac{ 1}{6s}+\frac{3}{2(s+2)}+\frac{-5}{3(s+3)}F(s)=6s1​+2(s+2)3​+3(s+3)−5​

F(s)F(s)F(s) 拉式反变换为 f(t)=(16+32e−2t−53e−3t)ϵ(t)f(t)=( \frac{ 1}{6}+\frac{3}{2}e^{-2t}-\frac{5}{3}e^{-3t})\epsilon(t)f(t)=(61​+23​e−2t−35​e−3t)ϵ(t)

解：设左边加法器输出为：X(s)X(s)X(s)

则：X(s)=F(s)−5s−1X(s)−4s−2X(s)X(s)=F(s)-5s^{-1}X(s)-4s^{-2}X(s)X(s)=F(s)−5s−1X(s)−4s−2X(s)

Y(s)=X(s)+4s−2X(s)Y(s)=X(s)+4s^{-2}X(s)Y(s)=X(s)+4s−2X(s)

可得：X(s)=s2s2+5s+4F(s)X(s)=\frac{s^2}{s^2+5s+4}F(s)X(s)=s2+5s+4s2​F(s)
Y(s)=s2+4s2+5s+4F(s),即：(s2+5s+4)Y(s)=(s2+4)F(s)Y(s)=\frac{s^2+4}{s^2+5s+4}F(s),即：({s^2+5s+4})Y(s)=(s^2+4)F(s)Y(s)=s2+5s+4s2+4​F(s),即：(s2+5s+4)Y(s)=(s2+4)F(s)

（1）微分方程：y′′(t)+5y′(t)+4y(t)=f′′(t)+4f(t)y''(t)+5y'(t)+4y(t)=f''(t)+4f(t)y′′(t)+5y′(t)+4y(t)=f′′(t)+4f(t)

（2）系统函数：H(s)=s2+4s2+5s+4H(s)=\frac{s^2+4}{s^2+5s+4}H(s)=s2+5s+4s2+4​

（3）H(s)=s2+4s2+5s+4=1+53(s+1)−203(s+4)H(s)=\frac{s^2+4}{s^2+5s+4}=1+\frac{5}{3(s+1)}-\frac{20}{3(s+4)}H(s)=s2+5s+4s2+4​=1+3(s+1)5​−3(s+4)20​
h(t)=L−1[H(s)]=δ(t)+(53e−t−203e−4t)ϵ(t)h(t)=\mathcal{L^{-1}}[H(s)]=\delta(t)+(\frac{5}{3}e^{-t}-\frac{20}{3}e^{-4t})\epsilon(t)h(t)=L−1[H(s)]=δ(t)+(35​e−t−320​e−4t)ϵ(t)

学习通考试60分钟没能做得完，还是练得少了，拿到题目不知如何下手，博客上重新写一遍，有点感觉了，practisepractisepractise makesmakesmakes perfectperfectperfect ！！！不要眼高手低，多练，多练，多练！


先赞后看，养成习惯！！！^ _ ^ ❤️ ❤️ ❤️
码字不易，大家的支持就是我坚持下去的动力。点赞后不要忘了关注我哦！

频域 系统