python scipy 稀疏矩阵的使用说明
是最简单的稀疏矩阵存储方式,采用三元组(row, col, data)(或称为ijv format)的形式来存储矩阵中非零元素的信息。
在实际使用中,一般coo_matrix用来创建矩阵,因为coo_matrix无法对矩阵的元素进行增删改操作;创建成功之后可以转化成其他格式的稀疏矩阵(如csr_matrix、csc_matrix)进行转置、矩阵乘法等操作。
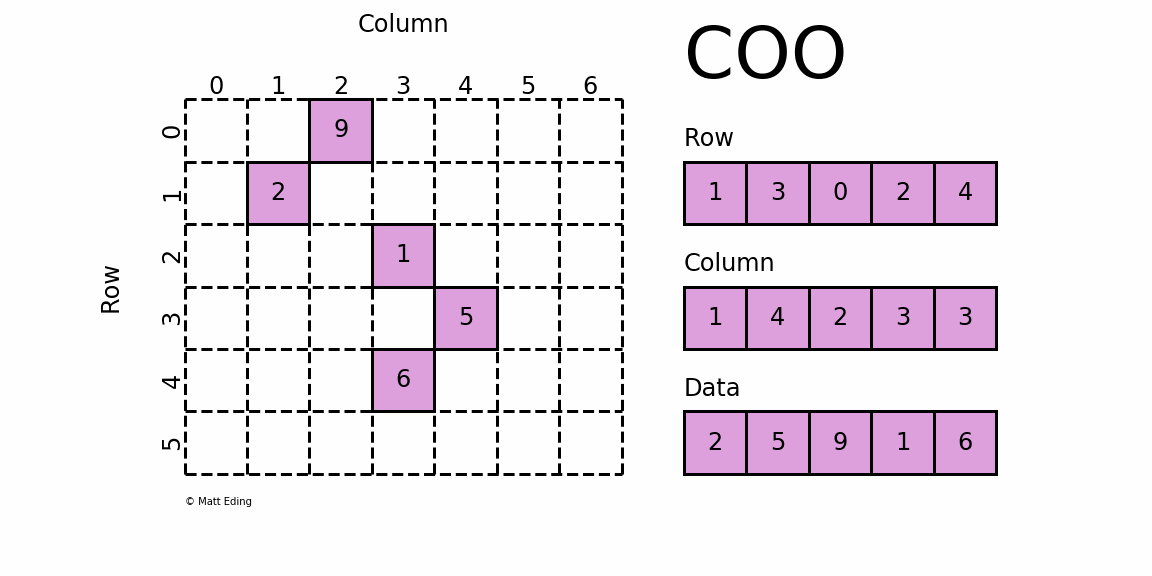
coo_matrix可以通过四种方式实例化,除了可以通过coo_matrix(D), D代表密集矩阵;coo_matrix(S), S代表其他类型稀疏矩阵或者coo_matrix((M, N), [dtype])构建一个shape为M*N的空矩阵,默认数据类型是d,还可以通过(row, col, data)三元组初始化:
>>> import numpy as np
>>> from scipy.sparse import coo_matrix
>>> _row = np.array([0, 3, 1, 0])
>>> _col = np.array([0, 3, 1, 2])
>>> _data = np.array([4, 5, 7, 9])
>>> coo = coo_matrix((_data, (_row, _col)), shape=(4, 4), dtype=np.int)
>>> coo.todense() # 通过toarray方法转化成密集矩阵(numpy.matrix)
>>> coo.toarray() # 通过toarray方法转化成密集矩阵(numpy.ndarray)
array([[4, 0, 9, 0],
[0, 7, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 5]])
上面通过triplet format的形式构建了一个coo_matrix对象,我们可以看到坐标点(0,0)对应值为4,坐标点(1,1)对应值为7等等,这就是coo_matrix。coo_matrix对象有很多方法,大多数是elementwise的操作函数;coo_matrix对象有以下属性:
dtype dtype
矩阵中元素的数据类型
shape 2-tuple
获取矩阵的shape
ndim int
获取矩阵的维度,当然值是2咯
nnz
存储值的个数,包括显示声明的零元素(注意)
data
稀疏矩阵存储的值,是一个一维数组,即上面例子中的_data
row
与data同等长度的一维数组,表征data中每个元素的行号
col
与data同等长度的一维数组,表征data中每个元素的列号
在实际应用中,coo_matrix矩阵文件通常存成以下形式,表示稀疏矩阵是coo_matrix(coordinate),由13885行1列组成,共有949个元素值为非零,数据类型为整形。
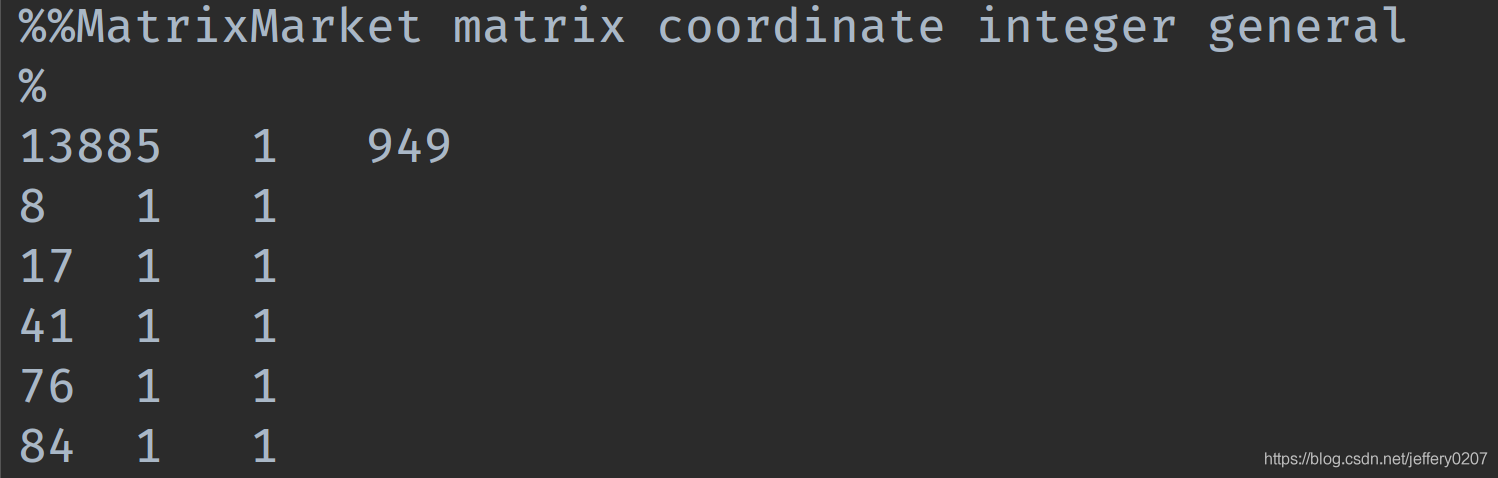
下面给出coo_matrix矩阵文件读写示例代码,mmread()用于读取稀疏矩阵,mmwrite()用于写入稀疏矩阵,mminfo()用于查看稀疏矩阵文件元信息。(这三个函数的操作不仅仅限于coo_matrix)
from scipy.io import mmread, mmwrite, mminfo
HERE = dirname(__file__)
coo_mtx_path = join(HERE, 'data/matrix.mtx')
coo_mtx = mmread(coo_mtx_path)
print(mminfo(coo_mtx_path))
# (13885, 1, 949, 'coordinate', 'integer', 'general')
# (rows, cols, entries, format, field, symmetry)
mmwrite(join(HERE, 'data/saved_mtx.mtx'), coo_mtx)
coo_matrix的优点:
有利于稀疏格式之间的快速转换(tobsr()、tocsr()、to_csc()、to_dia()、to_dok()、to_lil())
允许又重复项(格式转换的时候自动相加)
能与CSR / CSC格式的快速转换
coo_matrix的缺点:
不能直接进行算术运算
csr_matrix csr_matrix,全称Compressed Sparse Row matrix,即按行压缩的稀疏矩阵存储方式,由三个一维数组indptr, indices, data组成。
这种格式要求矩阵元按行顺序存储,每一行中的元素可以乱序存储。
那么对于每一行就只需要用一个指针表示该行元素的起始位置即可。
indptr存储每一行数据元素的起始位置,indices这是存储每行中数据的列号,与data中的元素一一对应。
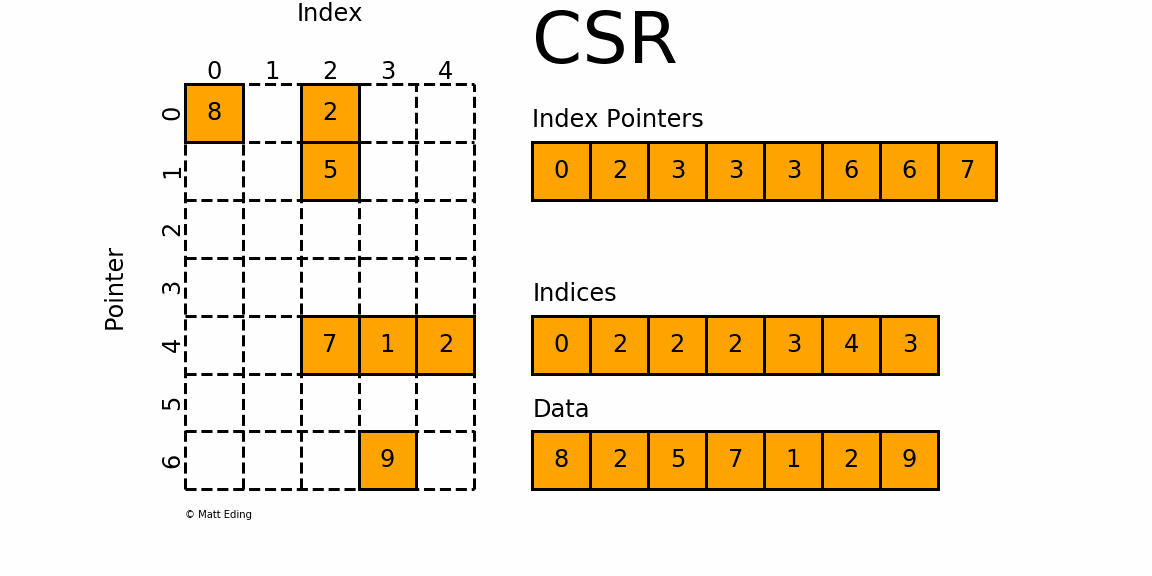
csr_matrix可用于各种算术运算:它支持加法,减法,乘法,除法和矩阵幂等操作。
其有五种实例化方法,其中前四种初始化方法类似coo_matrix,即通过密集矩阵构建、通过其他类型稀疏矩阵转化、构建一定shape的空矩阵、通过(row, col, data)构建矩阵。
其第五种初始化方式这是直接体现csr_matrix的存储特征:csr_matrix((data, indices, indptr), [shape=(M, N)]),意思是,矩阵中第i行非零元素的列号为indices[indptr[i]:indptr[i+1]],相应的值为data[indptr[i]:indptr[i+1]]
举个例子:
>>> import numpy as np
>>> from scipy.sparse import csr_matrix
>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> csr = csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 2],
[0, 0, 3],
[4, 5, 6]])
csr_matrix同样有很多方法,其中tobytes(),tolist(), tofile(),tostring()值得注意,其他具体参考官方文档,csr_matrix对象属性前五个同coo_matrix,另外还有属性如下:
indices
与属性data一一对应,元素值代表在某一行的列号
indptr
csr_matrix各行的起始值,length(csr_object.indptr) == csr_object.shape[0] + 1
has_sorted_indices
判断每一行的indices是否是有序的,返回bool值
csr_matrix的优点:
高效的算术运算CSR + CSR,CSR * CSR等高效的行切片快速矩阵运算
csr_matrix的缺点:
列切片操作比较慢(考虑csc_matrix)稀疏结构的转换比较慢(考虑lil_matrix或doc_matrix)
csc_matrix csc_matrix和csr_matrix正好相反,即按列压缩的稀疏矩阵存储方式,同样由三个一维数组indptr, indices, data组成,如下图所示:
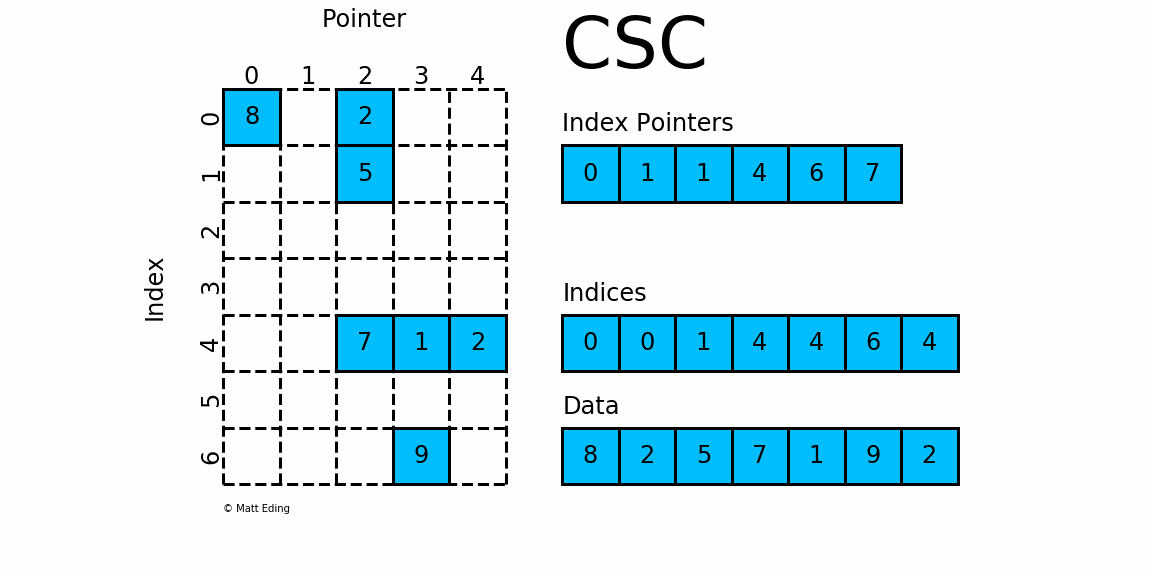
其实例化方式、属性、方法、优缺点和csr_matrix基本一致,这里不再赘述,它们之间唯一的区别就是按行或按列压缩进行存储。
而这一区别决定了csr_matrix擅长行操作;csc_matrix擅长列操作,进行运算时需要进行合理存储结构的选择。
lil_matrix lil_matrix,即List of Lists format,又称为Row-based linked list sparse matrix。它使用两个嵌套列表存储稀疏矩阵:data保存每行中的非零元素的值,rows保存每行非零元素所在的列号(列号是顺序排序的)。
这种格式很适合逐个添加元素,并且能快速获取行相关的数据。
其初始化方式同coo_matrix初始化的前三种方式:通过密集矩阵构建、通过其他矩阵转化以及构建一个一定shape的空矩阵。
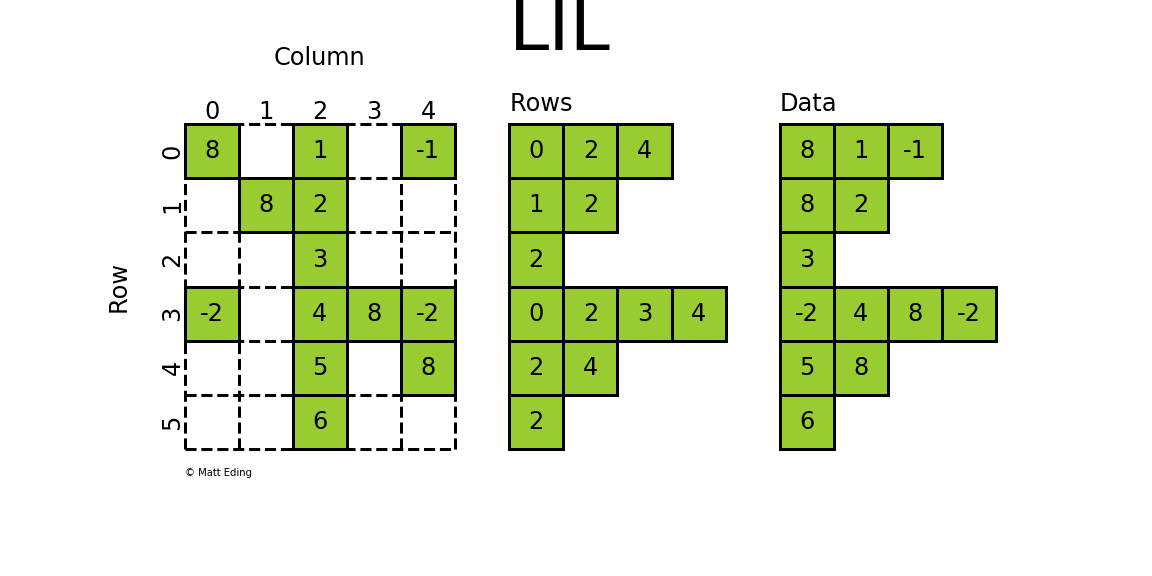
lil_matrix可用于算术运算:支持加法,减法,乘法,除法和矩阵幂。其属性前五个同coo_matrix,另外还有rows属性,是一个嵌套List,表示矩阵每行中非零元素的列号。
LIL matrix本身的设计是用来方便快捷构建稀疏矩阵实例,而算术运算、矩阵运算则转化成CSC、CSR格式再进行,构建大型的稀疏矩阵还是推荐使用COO格式。
LIL format优点
支持灵活的切片操作行切片操作效率高,列切片效率低
稀疏矩阵格式之间的转化很高效(tobsr()、tocsr()、to_csc()、to_dia()、to_dok()、to_lil())
LIL format缺点
加法操作效率低 (consider CSR or CSC)
列切片效率低(consider CSC)
矩阵乘法效率低 (consider CSR or CSC)
dok_matrix dok_matrix,即Dictionary Of Keys based sparse matrix,是一种类似于coo matrix但又基于字典的稀疏矩阵存储方式,key由非零元素的的坐标值tuple(row, column)组成,value则代表数据值。
dok matrix非常适合于增量构建稀疏矩阵,并一旦构建,就可以快速地转换为coo_matrix。
其属性和coo_matrix前四项同;其初始化方式同coo_matrix初始化的前三种:通过密集矩阵构建、通过其他矩阵转化以及构建一个一定shape的空矩阵。
对于dok matrix,可用于算术运算:它支持加法,减法,乘法,除法和矩阵幂;允许对单个元素进行快速访问( O(1) ); 不允许重复。
>>> import numpy as np
>>> from scipy.sparse import dok_matrix
>>> np.random.seed(10)
>>> matrix = random(3, 3, format='dok', density=0.4)
>>> matrix[1, 1] = 33
>>> matrix[2, 1] = 10
>>> matrix.toarray()
array([[ 0. , 0. , 0. ],
[ 0. , 33. , 0. ],
[ 0.19806286, 10. , 0.22479665]])
>>> dict(matrix)
{(2, 0): 0.19806286475962398, (2, 1): 10.0, (2, 2): 0.22479664553084766, (1, 1): 33.0}
>>> isinstance(matrix, dict)
True
在上面代码最后可以看到,实际上dok_matrix实例也是dict实例,在实现上继承了dict类。
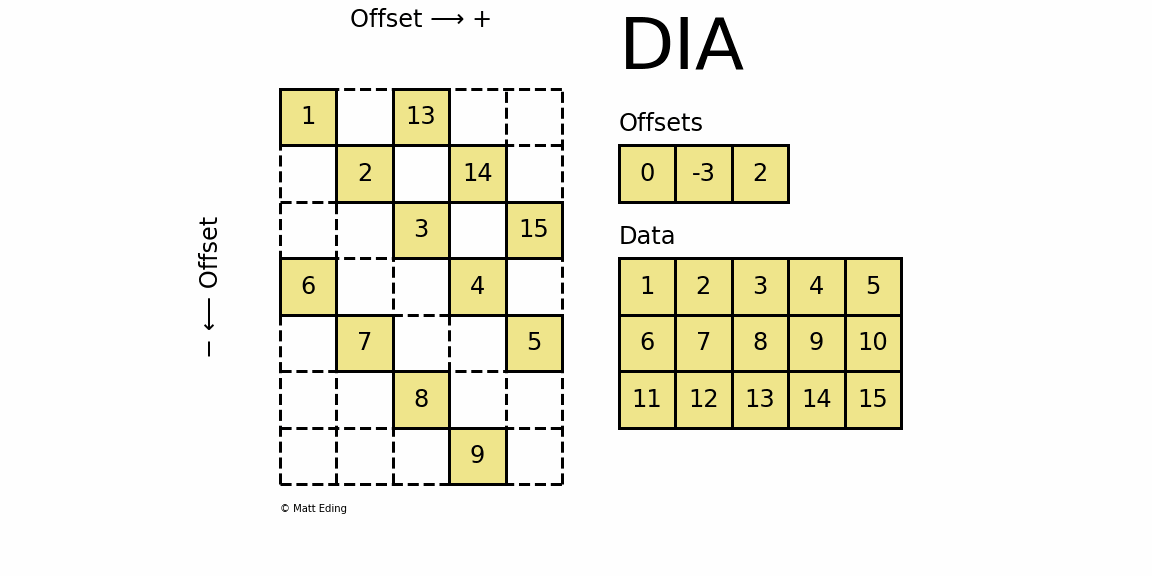
dia_matrix dia_matrix,全称Sparse matrix with DIAgonal storage,是一种对角线的存储方式。
如下图中,将稀疏矩阵使用offsets和data两个矩阵来表示。offsets表示data中每一行数据在原始稀疏矩阵中的对角线位置k(k>0, 对角线往右上角移动;k<0, 对角线往左下方移动;k=0,主对角线)。
该格式的稀疏矩阵可用于算术运算:它们支持加法,减法,乘法,除法和矩阵幂。
dia_matrix五个属性同coo matrix, 另外还有属性offsets;dia_matrix有四种初始化方式,其中前三种初始化方式同coo_matrix前三种初始化方式,即:通过密集矩阵构建、通过其他矩阵转化以及构建一个一定shape的空矩阵。
第四种初始化方式如下:
dia_matrix((data, offsets), shape=(M, N)) ,
其中,data[k,:]存储着稀疏矩阵offsets[k]对角线上的值
>>> data = np.arange(15).reshape(3, -1) + 1
>>> offsets = np.array([0, -3, 2])
>>> dia = sparse.dia_matrix((data, offsets), shape=(7, 5))
>>> dia.toarray()
array([[ 1, 0, 13, 0, 0],
[ 0, 2, 0, 14, 0],
[ 0, 0, 3, 0, 15],
[ 6, 0, 0, 4, 0],
[ 0, 7, 0, 0, 5],
[ 0, 0, 8, 0, 0],
[ 0, 0, 0, 9, 0]])
不是很常用,了解即可
bsr_matrix bsr_matrix,全称Block Sparse Row matrix,这种压缩方式极其类似CSR格式,但使用分块的思想对稀疏矩阵进行按行压缩。所以,BSR适用于具有dense子矩阵的稀疏矩阵。该种矩阵有五种初始化方式,分别如下:
bsr_matrix(D, [blocksize=(R,C)])
D是一个M*N的二维dense矩阵;blocksize需要满足条件:M % R = 0和N % C = 0,若不给定该参数,内部将会应用启发式的算法自动决定一个合适的blocksize.
bsr_matrix(S, [blocksize=(R,C)])
S是指其他类型的稀疏矩阵
bsr_matrix((M, N), [blocksize=(R,C), dtype])
构建一个shape为M*N的空矩阵
bsr_matrix((data, ij), [blocksize=(R,C), shape=(M, N)])
data 和ij 满足条件: a[ij[0, k], ij[1, k]] = data[k]
bsr_matrix((data, indices, indptr), [shape=(M, N)])
data.shape一般是k*R*C,其中R、C分别代表block的行和列长,k代表有几个小block矩阵;第i行的块列索引存储在indices[indptr[i]:indptr[i+1]],其值是data[ indptr[i]: indptr[i+1] ]。
bsr_matrix可用于算术运算:支持加法,减法,乘法,除法和矩阵幂。如下面的例子,对于许多稀疏算术运算,BSR比CSR和CSC更有效:
>>> from scipy.sparse import bsr_matrix
>>> import numpy
>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6]).repeat(4).reshape(6, 2, 2)
>>> bsr_matrix((data,indices,indptr), shape=(6, 6)).toarray()
array([[1, 1, 0, 0, 2, 2],
[1, 1, 0, 0, 2, 2],
[0, 0, 0, 0, 3, 3],
[0, 0, 0, 0, 3, 3],
[4, 4, 5, 5, 6, 6],
[4, 4, 5, 5, 6, 6]])
可以通过热图观察矩阵有没有明显分块模式再决定使不使用该方式
bsr matrix对象拥有9个属性,前四个属性与coo matrix相同,另外还有以下属性(注意csr matrix和bsr matrix之间的区别与联系):
data
即稀疏矩阵的数组,data.shape一般是k*R*C
indices
与属性data中的k个二维矩阵一一对应,元素值代表在某一行的列号
indptr
bsr各行起始起始值
blocksize
即tuple(R,C)
has_sorted_indices
判断每一行的indices是否是有序的,返回bool值
实用函数 构造特殊稀疏矩阵scipy.sparse模块还包含一些便捷函数,用于快速构建单位矩阵、对角矩阵等,下面做一个简单的汇总:
| identity(n[, dtype, format]) | 生成稀疏单位矩阵 |
| kron(A, B[, format]) | sparse matrices A 和 B的克罗内克积 |
| kronsum(A, B[, format]) | sparse matrices A 和 B的克罗内克和 |
| diags(diagonals[, offsets, shape, format, dtype]) | 构建稀疏对角阵 |
| spdiags(data, diags, m, n[, format]) | 构建稀疏对角阵,同上,但不可指定shape |
| block_diag(mats[, format, dtype]) | mats为iterable, 包含多个矩阵,根据mats构建块对角稀疏矩阵。 |
| tril(A[, k, format]) | 以稀疏格式返回矩阵的下三角部分 |
| triu(A[, k, format]) | 以稀疏格式返回矩阵的上三角部分 |
| bmat(blocks[, format, dtype]) | 从稀疏子块构建稀疏矩阵 |
| hstack(blocks[, format, dtype]) | 水平堆叠稀疏矩阵(column wise) |
| vstack(blocks[, format, dtype]) | 垂直堆叠稀疏矩阵 (row wise) |
| rand(m, n[, density, format, dtype, …]) | 使用均匀分布的值生成给定形状和密度的稀疏矩阵 |
| random(m, n[, density, format, dtype, …]) | 使用随机分布的值生成给定形状和密度的稀疏矩阵 |
| eye(m[, n, k, dtype, format]) | 生成稀疏单位对角阵(默认DIAgonal format) |
scipy.sparse.bmat举例:
In [1]: A = np.arange(8).reshape(2, 4)
In [2]: T = np.tri(5, 4)
In [3]: L = [[8] * 4] * 2
In [4]: I = sparse.identity(4)
In [5]: Z = sparse.coo_matrix((2, 3))
In [6]: sp.bmat([[ A, Z, L],
...: [None, None, I],
...: [ T, None, None]], dtype=int)
Out[7]:
<11x11 sparse matrix of type '<class 'numpy.int64'>'
with 33 stored elements in COOrdinate format>
In [8]: _.toarray() # ipython previous output
Out[9]:
array([[0, 1, 2, 3, 0, 0, 0, 8, 8, 8, 8],
[4, 5, 6, 7, 0, 0, 0, 8, 8, 8, 8],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0]])
稀疏矩阵类型判断
scipy.sparse模块还包含一些判断稀疏矩阵类型的函数,这里需要注意的是,issparse() 和 isspmatrix() 是相同的函数,也许是由于历史原因保留下来了两个。
isspars(x)
isspmatrix(x)
isspmatrix_csc(x)
isspmatrix_csr(x)
isspmatrix_bsr(x)
isspmatrix_lil(x)
isspmatrix_dok(x)
isspmatrix_coo(x)
isspmatrix_dia(x)
稀疏矩阵存取
load_npz(file) 从.npz文件中读取稀疏矩阵
save_npz(file, matrix[,compressed]) 将稀疏矩阵写入.npz文件中
其他
find(A) 返回稀疏矩阵中非零元素的索引以及值
经验总结要有效地构造矩阵,请使用dok_matrix或lil_matrix
lil_matrix类支持基本切片和花式索引,其语法与NumPy Array类似;lil_matrix形式是基于row的,因此能够很高效的转为csr,但是转为csc效率相对较低。
强烈建议不要直接使用NumPy函数运算稀疏矩阵
如果你想将NumPy函数应用于这些矩阵,首先要检查SciPy是否有自己的给定稀疏矩阵类的实现,或者首先将稀疏矩阵转换为NumPy数组(使用类的toarray()方法)。
要执行乘法或转置等操作,首先将矩阵转换为CSC或CSR格式,效率高
CSR格式特别适用于快速矩阵矢量产品
CSR,CSC和COO格式之间的所有转换都是线性复杂度。
以上为个人经验,希望能给大家一个参考,也希望大家多多支持软件开发网。