（kaldi、matlab、自己编写的）三种不同方式得到的mfcc数据之性能比较

（kaldi、matlab、自己编写的）三种不同方式得到的mfcc数据之性能比较1.绘制kaldi方式提取出的mfcc特征值1.1 将本地的mfcc数据读入matlab2.绘制matlab调用函数产生的mfcc特征值2.1 求取帧长和帧移2.2 绘制结果&显示3.绘制自己编写的matlab函数提取出来的mfcc特征值4.三种结果比较&结论
在之前的博客中分别实现了使用matlab编程获取wav语音数据的mfcc特征值、调用他人的方法获取mfcc方法、调用kaldi封装的mfcc函数进行特征值提取，那么究竟这三种方法哪种性能更优呢？也或者我们是否能在这个实验的比较中得到什么结果呢？
实验准备材料，本次实验将分别采用这三种方法，对同一语音数据进行测试，并将其进行特征值最后进行绘图表示，查看其具体差异。该语音信号是fs为16k,时长5s,内容为"中国加油"，接下来就让我们看下去吧~~ 1.绘制kaldi方式提取出的mfcc特征值

在开始本方法之前，我们需要先将之前通过kaldi方式产生的特征值读入到matlab。

1.1 将本地的mfcc数据读入matlab

因为之前产生得到是就是一个数据矩阵，所以matlab很轻易的就可以将文件读入，具体可以查看以下代码及结果：

%清除历史数据 clc; clear all %读入txt2.ark中的mfcc特征值 Y = load('txt2.ark'); y=Y(:,1); %获取mfcc特征矩阵的第一列 N=length(Y) x=1:1:N; set(gcf,'position',[180,160,960,600]);%设置画图的大小 plot(x,y); grid on;

很快我们即可得到其结果显示如下所示：

2.绘制matlab调用函数产生的mfcc特征值

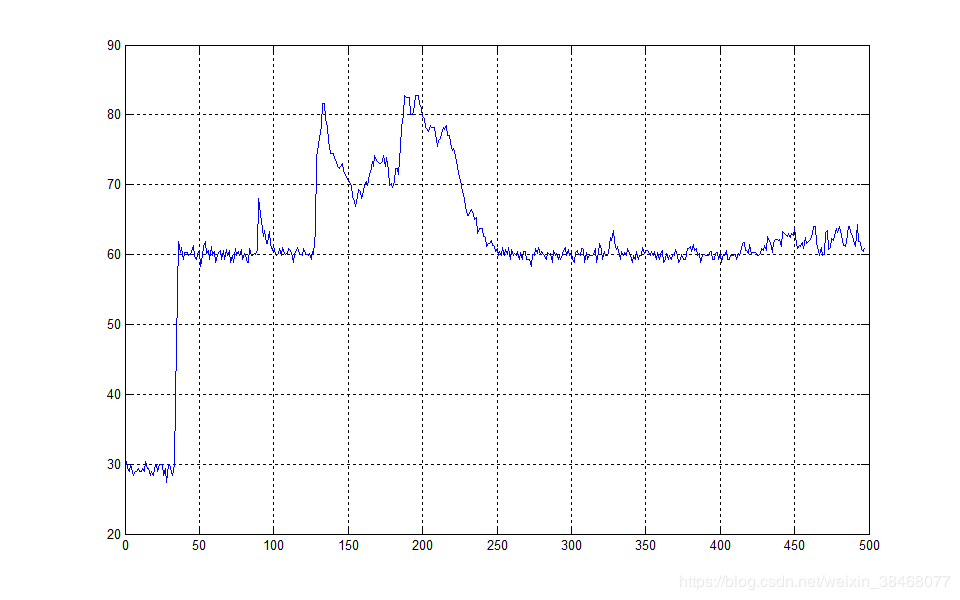
在这里还有一个问题就是为了确保该方式和kaldi方式产生的相同，换句话说就是要得到和kaldi方法相同的语音帧数，此刻我们还缺少两个参数，分别为每一帧的帧长和帧移。

2.1 求取帧长和帧移

通过matlab读取该语音文件我们得知该语音文件共含有79872个采样点，又因为kaildi得出的数据为497帧，于是为了计算出帧长和帧移，我们不妨设置如下等式：
(x−y)⋅496+x=49872 (x-y)\cdot496+x=49872 (x−y)⋅496+x=49872
式中字母xxx和yyy分别代表如下：

xxx代表帧长 yyy代表帧移

或许此刻你或许会说一个方程两个未知数，怎么可以得到结果呢？在这里我还要说明一点，因为在做语音分帧的时候帧的长度都是2的N次方，凭借着直觉，我将 x=512x=512x=512 带入方程，解得 y=160y=160y=160,并将这一组结果带入该函数，恰好得出我们需要的497帧语音数据。有了这个数据，我们便可以愉快的玩耍了。哈哈哈~~

2.2 绘制结果&显示

这里我直接调用的别人封装好的函数，并编辑了一下代码，如下：

[x1,fs]=audioread('test3.wav');%读取wav文件 %调用别人封装好的函数获取mfcc数据 ccc=Nmfcc(x1,fs,24,512,160);%mfcc特征值提取 %注意一下，这里的函数中需要传参，这里的512和160就是我们刚刚计算得出的数值。 %提取每一帧数据的第一列 xx=ccc(:,1)'; set(gcf,'position',[180,160,960,600]);%设置画图的大小 plot(xx); grid on;

执行完之后我们即可看到画出的波形图：

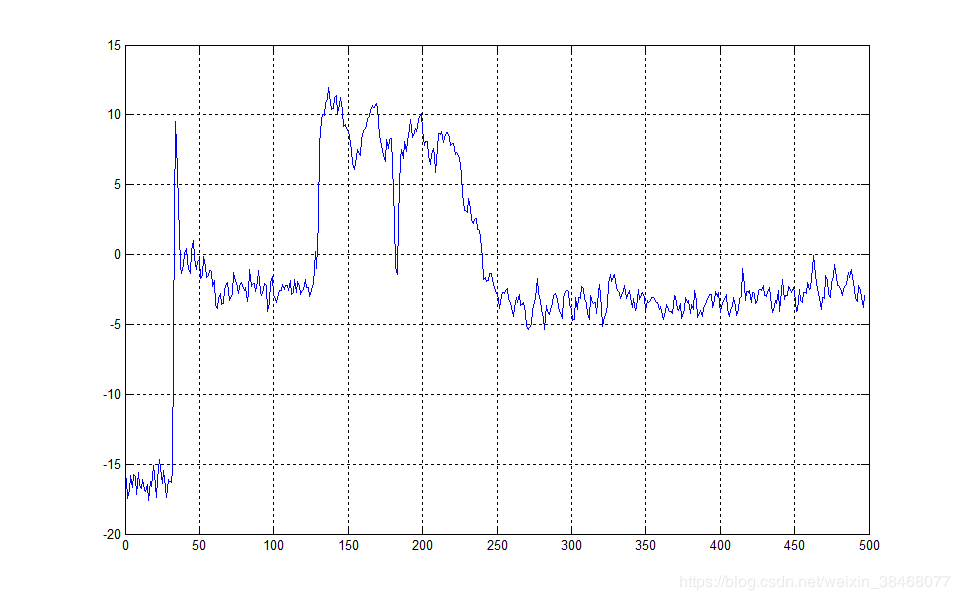
由于前边调用了别人写好的函数，但是我也对其封装函数进行了适当修改，这里我就将修改后的函数展示如下：

%MFCC计算函数 function ccc=Nmfcc(x,fs,p,frameSize,inc) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % function ccc=Nmfcc(x); % x是输入语音序列，Mel滤波器的个数为p，采样频率为fs，frameSize为帧长和FFT点数，inc为帧移；ccc为MFCC参数。 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 按帧长为frameSize，Mel滤波器的个数为p，采样频率为fs % 提取Mel滤波器参数，用汉明窗函数 bank=melbankm(p,frameSize,fs,0,0.5,'m'); % 归一化Mel滤波器组系数 bank=full(bank); bank=bank/max(bank(:)); % DCT系数,12*p for k=1:13 n=0:p-1; dctcoef(k,:)=cos((2*n+1)*k*pi/(2*p)); end % 归一化倒谱提升窗口 w = 1 + 6 * sin(pi * [1:13] ./ 12); w = w/max(w); % 预加重滤波器 xx=double(x); xx=filter([1 -0.9375],1,xx); % 语音信号分帧 xx=enframe(xx,frameSize,inc); n2=fix(frameSize/2)+1; % 计算每帧的MFCC参数 for i=1:size(xx,1) y = xx(i,:); s = y' .* hamming(frameSize); t = abs(fft(s)); t = t.^2; c1=dctcoef * log(bank * t(1:n2)); c2 = c1.*w'; m(i,:)=c2'; end %差分系数 dtm = zeros(size(m)); for i=3:size(m,1)-2 dtm(i,:) = -2*m(i-2,:) - m(i-1,:) + m(i+1,:) + 2*m(i+2,:); end dtm = dtm / 3; %求取二阶差分系数 dttm = zeros(size(dtm)); for i=3:size(m,1)-2 dttm(i,:) = -2*dtm(i-2,:) - dtm(i-1,:) + dtm(i+1,:) + 2*dtm(i+2,:); end dttm = dttm / 3; %合并MFCC参数、一阶差分MFCC参数、二阶差分MFCC参数 ccc = [m dtm]; %去除首尾两帧，因为这两帧的一阶差分参数为0 %ccc = ccc(3:size(m,1)-2,:); 3.绘制自己编写的matlab函数提取出来的mfcc特征值

这里我们需要调用自己之前写过的一个获取mfcc特征值的函数，来与之前的两种方式得出的数据进行对比，在这里我还需要说一下，因为函数是自己写的，基本没调用什么函数，所以代码量而言，就比其它两种方式的多很多。

%得到返回结果 myMfcc=Mymfcc(); %获取矩阵的第一列 xxx=myMfcc(:,1)'; %开始绘制图像 set(gcf,'position',[180,160,960,600]);%设置画图的大小 plot(xxx); grid on;

这里我对自己的函数进行了一下封装，大家可以来看一下效果：

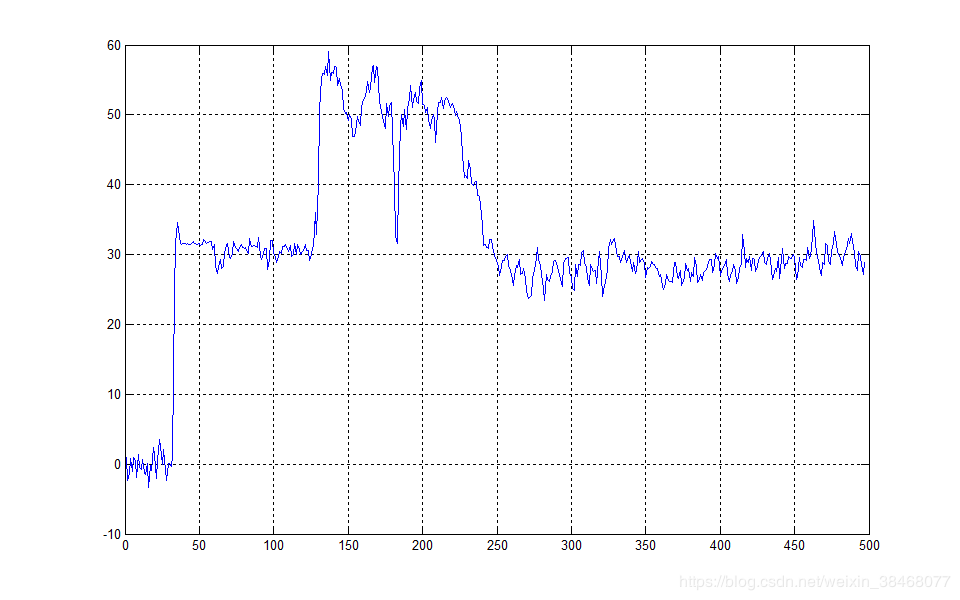
当然其中大部分的工作都在下边的函数里边，其内容如下：

function [mfcc_final]=Mymfcc() frameSize=512; inc=160; [x,fs]=audioread('test3.wav');%读取wav文件 N=length(x); %预加重y=x(i)-0.97*x(i-1) for i=2:N y(i)=x(i)-0.97*x(i-1); end y=y';%对y取转置 S=enframe(x,frameSize,inc);%分帧,对x进行分帧， [a b]=size(S); %尝试一下汉明窗a=0.46,得到汉明窗W=(1-a)-a*cos(2*pi*n/N) n=1:b; W=0.54-0.46*cos((2*pi.*n)/b); %创建汉明窗矩阵C C=zeros(a,b); ham=hamming(b); for i=1:a C(i,:)=ham; end %将汉明窗C和S相乘得SC SC=S.*C; %对SC的每一帧都进行N=4096的快速傅里叶变换,得到一个301*4096的矩阵 F=0;N=4096; for i=1:a %对SC作N=4096的FFT变换 D(i,:)=fft(SC(i,:),N); %以下循环实现求取能量谱密度E for j=1:N t=abs(D(i,j)); E(i,j)=(t^2)/N; end %获取每一帧的能量总和F(i) F(i)=sum(D(i,:)); end %开始计算谱熵 %求取P_i(k) P=zeros(a,4096); for i=1:a sum1=0; for t=1:N sum1=sum1+E(i,t); end for j=1:N P(i,j)=(E(i,j))/(sum1); end end %算出每一帧的谱熵H(i) for i=1:a sum1=0; for j=1:N sum1=sum1+P(i,j)*log(P(i,j)); end HH(i)=-sum1; end %计算谱熵结束 %将频率转换为梅尔频率 %梅尔频率转化函数图像 N1=length(x) for i=1:N1 mel(i)=2595*log10(1+i/700); end fl=0;fh=fs/2;%定义频率范围，低频和高频 bl=2595*log10(1+fl/700);%得到梅尔刻度的最小值 bh=2595*log10(1+fh/700);%得到梅尔刻度的最大值 %梅尔坐标范围 p=26;%滤波器个数 B=bh-bl;%梅尔刻度长度 mm=linspace(0,B,p+2);%规划28个不同的梅尔刻度 fm=700*(10.^(mm/2595)-1);%将Mel频率转换为频率 W2=N/2+1;%fs/2内对应的FFT点数,2049个频率分量 k=((N+1)*fm)/fs%计算28个不同的k值 hm=zeros(26,N);%创建hm矩阵 df=fs/N; freq=(0:N-1)*df;%采样频率值 %绘制梅尔滤波器 for i=2:27 %取整，这里取得是28个k中的第2-27个，舍弃0和28 n0=floor(k(i-1)); n1=floor(k(i)); n2=floor(k(i+1)); %要知道k(i)分别代表的是每个梅尔值在新的范围内的映射，其取值范围为：0-N/2 %以下实现公式--，求取三角滤波器的频率响应。 for j=1:N if n0<=j & j<=n1 hm(i-1,j)=2*(j-n0)/((n2-n0)*(n1-n0)); elseif n1<=j & j<=n2 hm(i-1,j)=2*(n2-j)/((n2-n0)*(n1-n0)); end end %此处求取H1(k)结束。 end %绘图,且每条颜色显示不一样 c=colormap(lines(26));%定义26条不同颜色的线条 set(gcf,'position',[180,160,1020,550]);%设置画图的大小 for i=1:26 plot(freq,hm(i,:),'--','color',c(i,:),'linewidth',2.5);%开始循环绘制每个梅尔滤波器 hold on end grid on;%显示方格 axis([0 1500 0 0.1]);%设置显示范围 %得到能量特征参数的和 H=E*hm'; %对H作自然对数运算 %因为人耳听到的声音与信号本身的大小是幂次方关系，所以要求个对数 for i=1:a for j=1:26 H(i,j)=log(H(i,j)); end end %作离散余弦变换 具体参考信号检测与估计的论文 for i=1:a for j=1:26 %先求取每一帧的能量总和 sum1=0; %作离散余弦变换 for p=1:26 sum1=sum1+H(i,p)*cos((pi*j)*(2*p-1)/(2*26)); end mfcc(i,j)=((2/26)^0.5)*sum1; %完成离散余弦变换 end end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%% 以下为求取mfcc的三个参数过程 %%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %作升倒谱运算 %因为大部分的信号数据一般集中在变换后的低频区，所以对每一帧只取前13个数据就好了 J=mfcc(:,(1:13)); %默认升到普系数为22 for i=1:13 K(i)=1+(22/2)*sin(pi*i/22); end %得到二维数组feat,这是mfcc的第一组数据，默认为三组 for i=1:a for j=1:13 L(i,j)=J(i,j)*K(j); end end feat=L; %接下来求取第二组（一阶差分系数）301x13 ，这也是mfcc参数的第二组参数 dtfeat=0; dtfeat=zeros(size(L));%默认初始化 for i=3:a-2 dtfeat(i,:)=-2*feat(i-2,:)-feat(i-1,:)+feat(i+1,:)+2*feat(i+2,:); end dtfeat=dtfeat/10; %求取二阶差分系数,mfcc参数的第三组参数 %二阶差分系数就是对前面产生的一阶差分系数dtfeat再次进行操作。 dttfeat=0; dttfeat=zeros(size(dtfeat));%默认初始化 for i=3:a-2 dttfeat(i,:)=-2*dtfeat(i-2,:)-dtfeat(i-1,:)+dtfeat(i+1,:)+2*dtfeat(i+2,:); end dttfeat=dttfeat/10; %这里的10是根据数据确定的，默认为2 %将得到的mfcc的三个参数feat、dtfeat、dttfeat拼接到一起 %得到最后的mfcc系数301x39 mfcc_final=0; mfcc_final=[feat,dtfeat,dttfeat];%拼接完成 4.三种结果比较&结论

在这之前我们已经将三种方式的得到的mfcc特征值分别进行了绘画，但是我们很难直接看出差别，于是在这一节，我们尝试将这三个显示在一张图中，从而比较其差别。

set(gcf,'position',[180,160,960,600]);%设置画图的大小 subplot(3,1,1); plot(y,'r','linewidth',1.5) grid on;title('kaldi生成的mfcc特征值','FontSize',15) subplot(3,1,2); plot(xx,'m','linewidth',1.5) grid on;title('调用matlab函数生成的mfcc特征值','FontSize',15) subplot(3,1,3); plot(xxx,'linewidth',1.5) grid on;title('自己编写的函数生成的mfcc特征值','FontSize',15)

说实话当我看到这个结果的时候还是有些惊诧的：

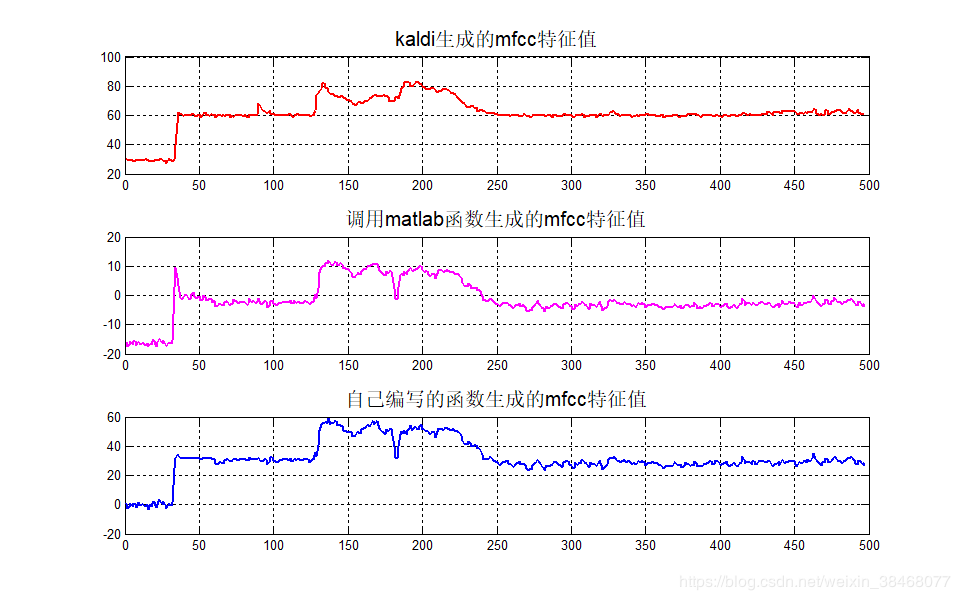
或许现在还看不出区别在哪里，但是我现在告诉你，这个测试的语音数据内容说的是"武汉加油"，四个字。这时候你可以再看一下其结果差异。我们可以看到后两种方法都依稀可以将这四个字判别开来，而kaldi产生的函数显然效果差些。再对其内容进行进一步分析：

%开始比较三种结果的差异 set(gcf,'position',[180,160,960,600]);%设置画图的大小 subplot(3,1,1); plot(y,'r','linewidth',1.5) grid on;title('kaldi生成的mfcc特征值','FontSize',15) axis([0 500 20 90]) hold on %画分割线 plot([126,126],[20,90],'g','linewidth',1.5); plot([153,153],[20,90],'g','linewidth',1.5); plot([183,183],[20,90],'g','linewidth',1.5); plot([208,208],[20,90],'g','linewidth',1.5); plot([245,245],[20,90],'g','linewidth',1.5); %写字 subplot(3,1,2); plot(xx,'m','linewidth',1.5) grid on;title('调用matlab函数生成的mfcc特征值','FontSize',15) hold on %画分割线 plot([126,126],[-20,20],'g','linewidth',1.5); plot([153,153],[-20,20],'g','linewidth',1.5); plot([183,183],[-20,20],'g','linewidth',1.5); plot([208,208],[-20,20],'g','linewidth',1.5); plot([245,245],[-20,20],'g','linewidth',1.5); %写字 hold off subplot(3,1,3); plot(xxx,'linewidth',1.5) grid on;title('自己编写的函数生成的mfcc特征值','FontSize',15) axis([0 500 -10 60]) hold on %画分割线 plot([126,126],[-10,60],'g','linewidth',1.5); plot([153,153],[-10,60],'g','linewidth',1.5); plot([183,183],[-10,60],'g','linewidth',1.5); plot([208,208],[-10,60],'g','linewidth',1.5); plot([245,245],[-10,60],'g','linewidth',1.5); %写字 text(128,20,'中','color','r','fontsize',20); text(155,20,'国','color','r','fontsize',20); text(185,20,'加','color','r','fontsize',20); text(213,20,'油','color','r','fontsize',20); hold off

其内容如下 所示：

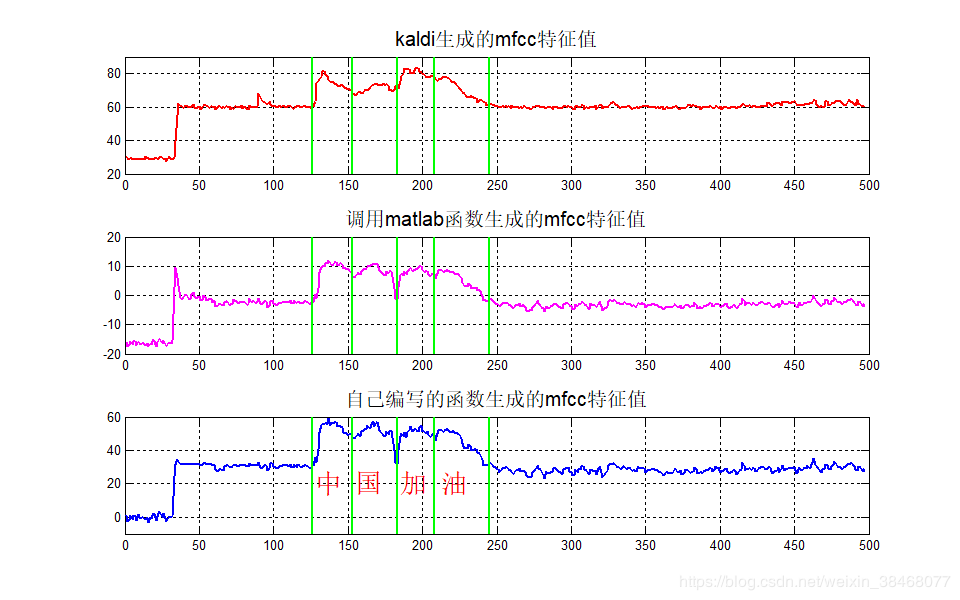
相信在上边的结果中我们可以清晰的看到，经过分析我也大致得到了以下结论：

kaldi产生的mfcc特征值在‘中‘，’国’这两个字处的波形与其它两个matlab函数生成的波形相差较大； 在kaldi产生的波形里边，在语音‘中’字之前出现了一个波峰，而在其它两个波形中均未出现； 调用matlab函数产生的那个波形，也就是第二个波形，在语音刚开始的那一段，峰值较高，与其它两个波形不一致； 还有一个问题需要指出的是如果单要比较这三个mfcc数据得到的速度的话，kaldi速度>调用matlab函数的速度>自己书写的函数的速度； 如果单从效果来说的话，自己书写的函数的效果>调用matlab函数的效果>kaldi的效果。

如果单从上边的的一条数据就得出一些结论，显然还是没有那么有说服力，接下来我又对其它两条语音数据进行了测试，这是语音文件“武汉加油”的波形显示。并且我还在该图中显示了语音信号的原始波形：

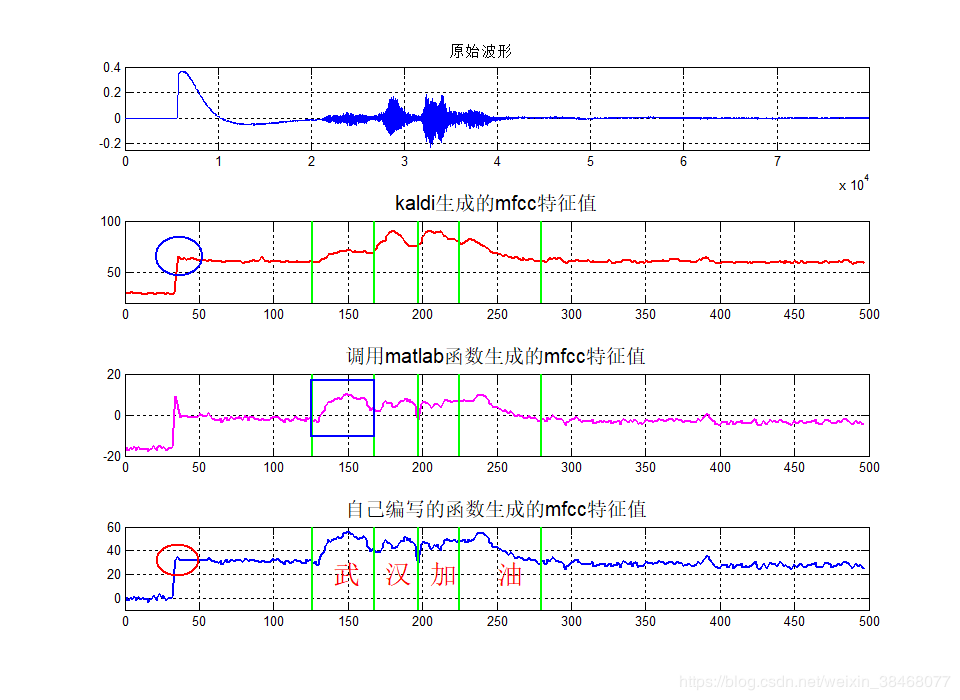
在上边的图示中我们可以发现我们之前说的那个异常波动点其实不是异常波动点，而是我们的原始语音信号中的噪声影响。再仔细分析就可发现，

三个波形中，是kaldi所生成的波形与原始波形一致性最高，但是语音开始的那段噪声并未明显显示; 调用别人matlab函数的波形图虽然将语音开始的那段噪声波动显示，但在”武“字的波形与kaldi的相差较大; 而自己编写的函数则集成了kaldi的缺点和别人matlab函数的缺点，着实有点悲哀。

无独有偶，测试另一个语音文件，该语音文件所说的是“你好，其问题就和我们刚刚总结的现象一致：如下所示

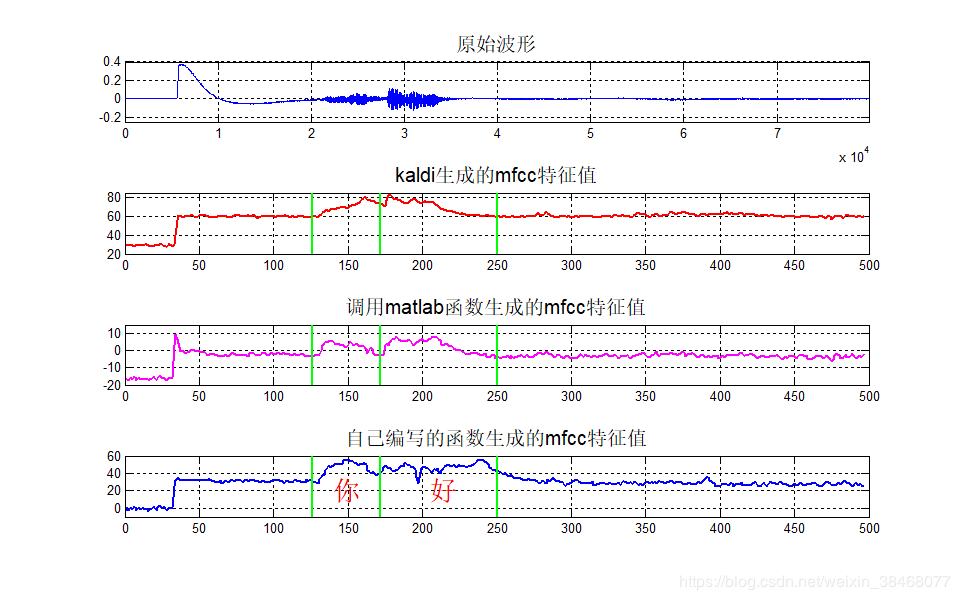
另外在这三个语音文件产生的几个波形图中，我们可以看到kaldi版本的波形与原始波形一致性较高，其次是调用matlab版本的调用其它函数所产生的数据，自己编写的函数则是与两者无论速度还是性能都与其它两种方法有差别，但是我并没有就此认输，我会查清楚kaldi版本所产生的数据准确度高的原因，并将在日后的研究中将差距原因再做总结。现在我再将此次实验得出的结果进行如下总结：

kaldi版本的特征值质量>调用别人函数的matlab版本的特征值质量>自己编写的； 两种matlab形式的在含有语音段的语音趋势与kaldi的和原始语音趋势有些许差距。

或许我在此做出的误差分析并不是真正的原因，如果各位读者有知道个中原因的，非常感谢您的指导，也欢迎大家一起讨论误差原因。

作者：王延凯的博客

性能 mfcc matlab kaldi