基于小波变换的图像边缘检测(matlab祖传代码注释)

上图为针对png格式无背景原图的边缘检测,对比各种边缘检测算子,小波变化的优势体现并不明显。

上图为针对含背景图片的边缘检测,小波变化的优势这里体现的比较明显。
相信看到这篇文章的小伙伴一定已经搜索了“小波变换 边缘检测”这样的关键词很多次了,但是得到的代码好像只有那一个,哈哈哈,我当时也是只发现了这一个代码,在查阅了一些文献后对代码思路有一些理解,在这里和大家分享~
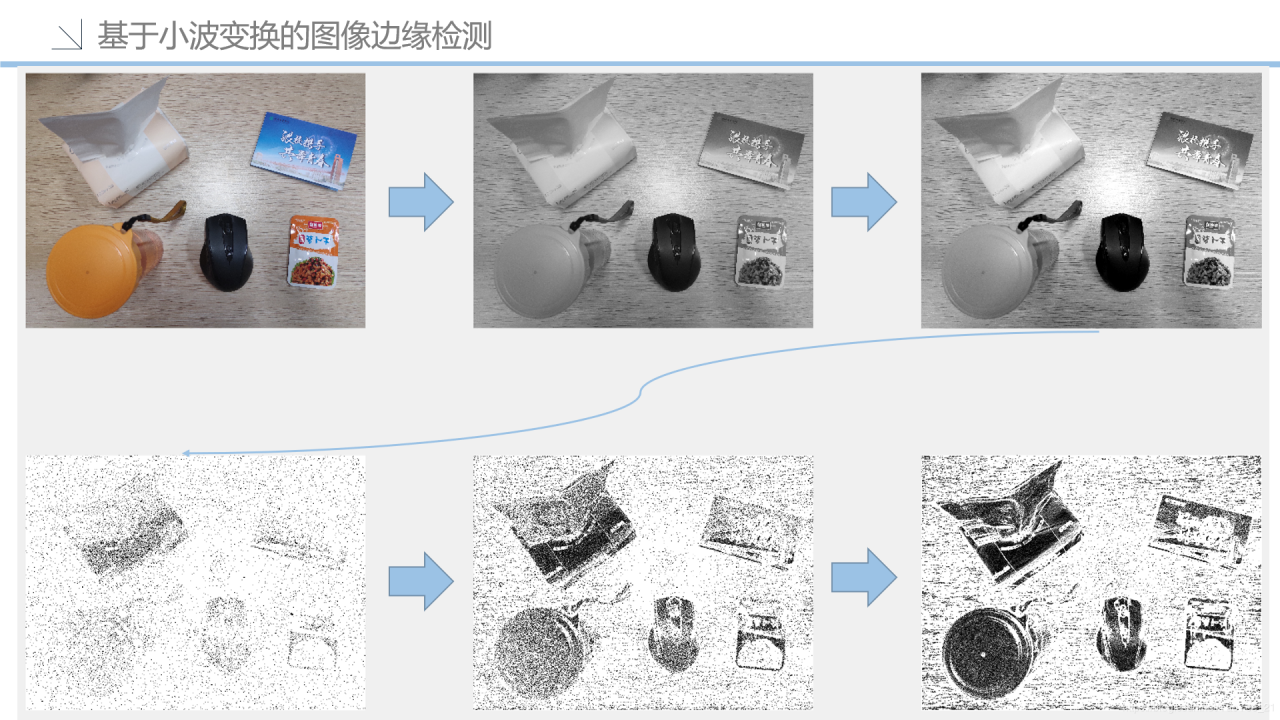
废话不多说,先放一张流程图便于大家理解代码。下面为加了一些注释的祖传代码。
clear all;
I = imread('E:\DAT\postgraudate\class\信号\matlab\test\retest.jpg'); %读取照片
subplot(2,3,1);
imshow(I);
I = rgb2gray(I);subplot(2,3,2);imshow(I); %彩色照片转灰度图
I1 = imadjust(I,stretchlim(I),[0,1]); %增强图片对比度,白的更白,黑的更黑
subplot(2,3,3);
imshow(I1);
[N,M] = size(I); %获取图片尺寸
h = [0.125,0.375,0.375,0.125]; %尺度向量 相当于低通滤波器
g = [0.5,-0.5]; %相当于高通滤波器
delta = [1,0,0];
J = 2; % 分解尺度
a(1:N,1:M,1,1:J+1) = 0; %初始化变量
dx(1:N,1:M,1,1:J+1) = 0; %x方向偏导初始化
dy(1:N,1:M,1,1:J+1) = 0; %y方向偏导初始化
d(1:N,1:M,1,1:J+1) = 0; % 模值初始化
a(:,:,1,1) = conv2(h,h,I,'same'); %卷积运算
dx(:,:,1,1) = conv2(delta,g,I,'same'); %计算x方向偏导
dy(:,:,1,1) = conv2(g,delta,I,'same'); %计算y方向偏导
x = dx(:,:,1,1);
y = dy(:,:,1,1);
d(:,:,1,1) = sqrt(x.^2+y.^2); %计算模值
I1 = imadjust(d(:,:,1,1),stretchlim(d(:,:,1,1)),[0 1]); %增强对比度
subplot(2,3,4);
imshow(I1);
lh = length(h);
lg = length(g);
for j = 1:J %按照分解尺度进行分解
lhj = 2^j*(lh-1)+1;
lgj = 2^j*(lg-1)+1;
hj(1:lhj)=0;
gj(1:lgj)=0;
for n = 1:lh
hj(2^j*(n-1)+1)=h(n);
end
for n = 1:lg
gj(2^j*(n-1)+1)=g(n);
end
a(:,:,1,j+1) = conv2(hj,hj,a(:,:,1,j),'same');
dx(:,:,1,j+1) = conv2(delta,gj,a(:,:,1,j),'same');
dy(:,:,1,j+1) = conv2(gj,delta,a(:,:,1,j),'same');
x = dx(:,:,1,j+1);
y = dy(:,:,1,j+1);
dj(:,:,1,j+1) = sqrt(x.^2+y.^2);
I1 = imadjust(dj(:,:,1,j+1),stretchlim(dj(:,:,1,j+1)),[0 1]);
%subplot(2,3,4+j);
figure();
imshow(I1);
end
%以下部分为噪点滤波,和小波变化无关
Icomp = imcomplement(I1); %反转图像
Ifilled = imfill(Icomp, 'holes');
se = strel('disk', 15); %小于此半径的连通域忽略掉
Iopenned = imopen(Ifilled, se);
%subplot(2,4,4+j+1);
figure();
imshow(Iopenned);
噪点滤波作用如下图所示
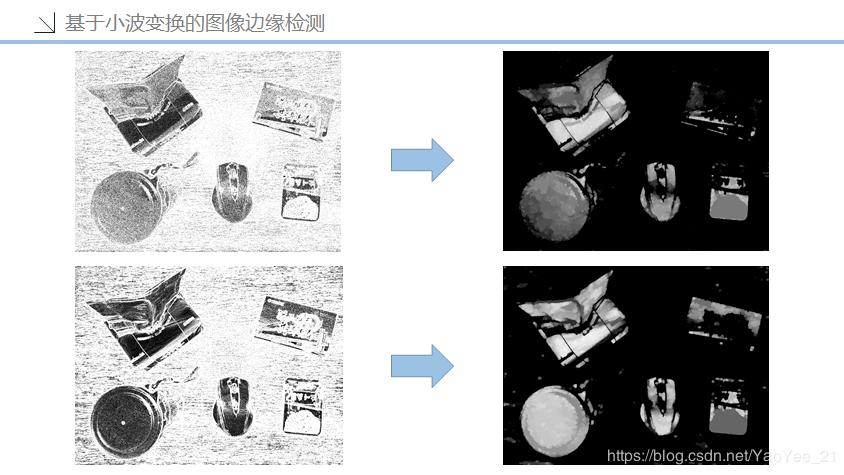
大家看到这里可能对每一行代码大概知道时什么意思了,但是整个代码段的逻辑结构可能还不清楚。就比如说,我现在去买菜,我知道了现在是我在给他钱,下一步是他找我钱,但是,我为毛要去买菜啊!这是个问题。
小波变换与尺度函数
时间多的,或者想融汇贯通这段代码的,点开上面这个链接,仔细看完,相信对你有很多帮助。我也是看了这篇文章对小波变换才知一二,没时间的,或者喜欢我的(哈哈哈)可以看我接下来的总结(扯淡)。
首先,小波变换分为连续小波变换和离散小波变换,由于我们用于计算的信号都是经过采样后的,所以接下来我们讲离散小波变化,同样代码里用的也是离散小波变换,这里可能有同学就要问了,为什么不用连续小波变换?是不是瞧不起我!
那么这里简单说一下,首先你怎么在代码里实现积分?如果有写过PID算法的同学可能知道,PID公式里也有积分,但是在代码里我们把他转变成了累加,这同时也是积分的意义,将坐标轴分成无限小的小段。。。扯远了
好的,现在我们确定使用离散小波变换了。
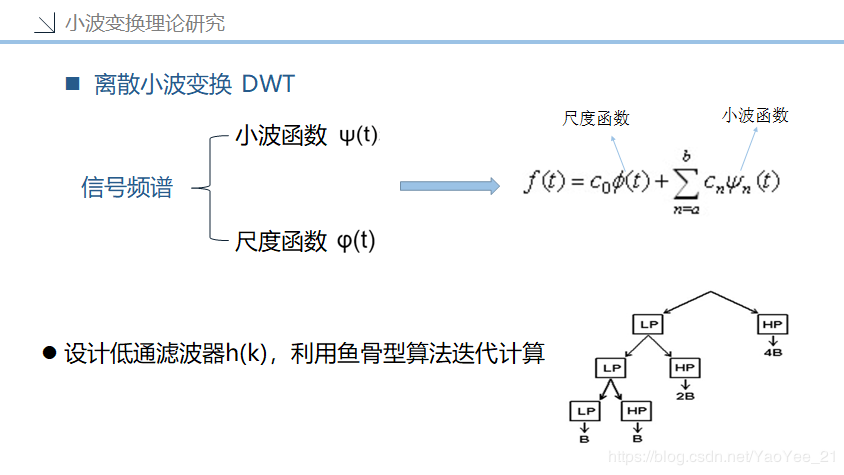
大家可以看到上图中信号输出 f(t) 等于后面的一串式子,那么我们怎么计算f(t)呢?
很简单,第一种方式,就按表达式算。那么我们是不是要有尺度函数和小波函数?那从哪得到呢?万能的淘宝也没有,需要自己构建,怎么构建呢?小波变换与尺度函数 这个链接又来啦,详见里面所述。总之就是太麻烦了,所以代码里采用第二种方式。
第二种方式,设计低通滤波器h(k),利用鱼骨型算法迭代计算。这个 h(k) 是什么呢?
h = [0.125,0.375,0.375,0.125];
没错,就是代码里这个参数,代表尺度向量,至于参数初始值为什么是这个,则需要根据尺度函数需要满足的3个条件来进行计算。
有了h和g后我们利用下面这个公式就可以一层层进行计算小波函数系数和尺度函数系数。

同样这两个公式在代码里也有体现。分解尺度 j 也就是我们代码里的循环次数。
到这里大家可能知道一些代码为什么是这样写了,知道我们原来买菜是为了做饭,那又为什么要做饭呢?这个问题还得大家一起去探讨。这里放几个我在学习小波变换的边缘检测中遇到的好文章,共享。
文章1 这篇文章就是文中放过的
文章2 这篇文章在讲相关参数 更深一点
文章3 这篇文章的5.2也有将代码思路
这篇文章是2019年10月6号写的,也是我在CSDN上写的第一篇文章,贡献了博客一半的访问量,今天是2020年2月6 号,这4个月期间也有断断续续了解一些小波变换边缘检测的新知识,比如说:
代码思路部分:祖传代码不完整,其输出是整个图像中每个像素点的模值,之后还要加一个寻找模极大值的部分,这样输出的模极大值才是图像边缘。
代码参数部分:滤波器的参数好像是B样条小波,那么整个小波变换所使用的小波基函数也就是B样条小波函数了。
有时候想重新写一篇博客,把现在的见解完整的写一遍,但是会发现不了解的东西还很多,小波变换比较新,虽然现在各行业应用的比较广泛,但是感觉教程不是很多,就像小波变换边缘检测全网好像就这一份代码。
努力吧,也不知道我什么时候可以摸透小波变换边缘检测,冲冲冲,也欢迎大家来找我交流,答疑和外包也可以。
个人QQ:1356580910,图像处理探索群:913931535 备注:CSDN
现在基于祖传代码加入了两种模极大值计算方法,一种需要手动调参,一种全自动计算。放一张现在的效果图吧(好像还可以)
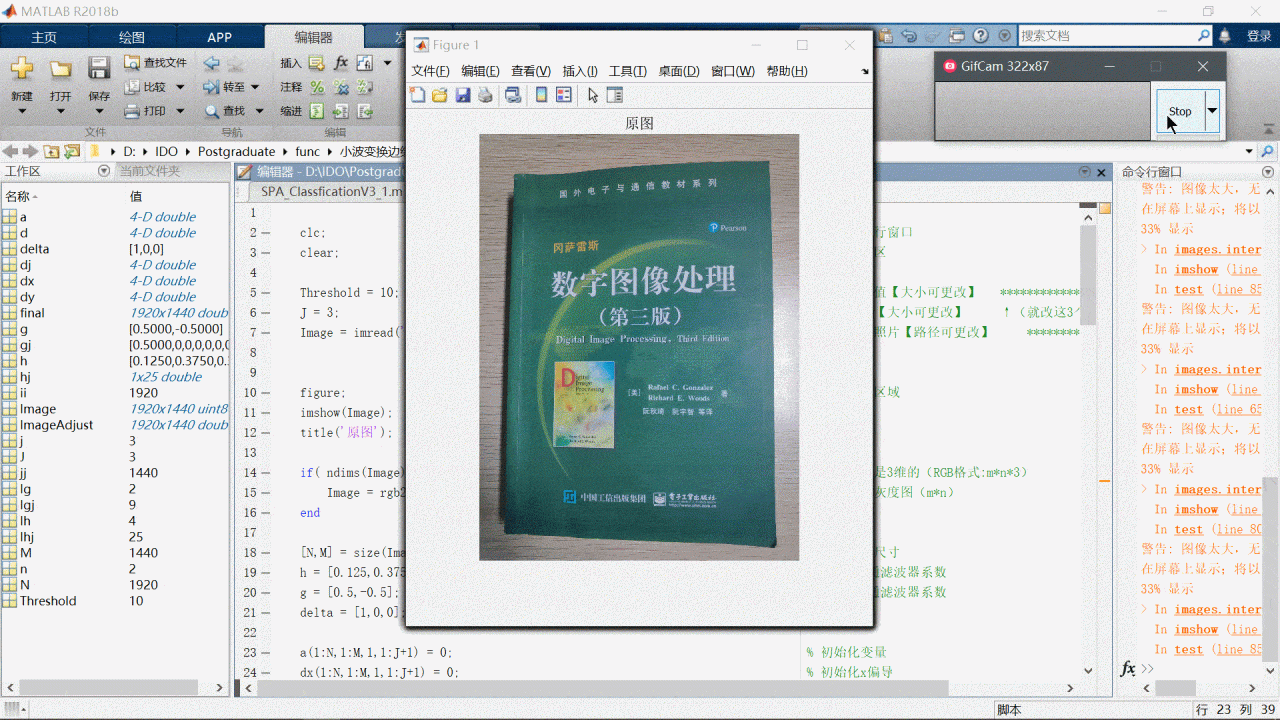
最后,希望赶快战胜疫情,我想上学了。
作者:YaoYee_7