【超详细！】周志华《机器学习》西瓜书 小白Python学习笔记（二）————第三章 线性模型 （对数几率回归）附课后题3.3详解

【超详细！】周志华《机器学习》西瓜书 小白Python学习笔记（二）——第三章 线性模型 （对数几率回归）附:课后题3.3详解回顾与前言第三章 线性模型对数几率回归课后习题3.3 回顾与前言

在上一篇博客中，我们通过小明习得“买瓜秘笈”的故事了解了机器学习的大概流程以及一些相应的基本术语。在接下来的文章中，我们将开始学习具体的机器学习算法啦！

学习什么知识模型都是一个从简到难的过程。很多时候未知的问题要通过将其分割成已经解决的问题，复杂的模型要通过简单模型的变形、组合来解决，比如说今天学习的线性模型看似很简单，非线性模型是通过映射等手段将其转化为线性模型而解决的；以及多分类问题也是将其分解成多个二分类问题而解决的。这是一种很经典的数学思维所以大家不要小看第三章 线性模型哦～

第三章 线性模型

对于第三章 线性模型我们主要将学习用途最广泛的对数几率回归的算法。
线性模型是最基本的模型，其基本形式是：
y=ax+by=ax+b y=ax+b
但是这种一维的形式实在是太简单了，于是我们从多维的线性模型开始，也就是将xxx以及系数都变成向量形式，即：
f(x)=wTx+bf(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+bf(x)=wTx+b
但是一般情况下，只有数值型的属性数据才能够放入模型进行回归。而实际问题中很多属性并不是通过数值表示的，比如上篇博客提到的西瓜的三个属性“色泽”“瓜蒂”“声响”是通过“光亮”“蜷缩”“浑浊”等词语表示的,标签“好瓜”“坏瓜”也是通过词语表示的。所以，我们要事先将这些属性、标签转化成数值型数据。

对于定序尺度的变量，比如{好瓜, 坏瓜}、{大,中,小}我们就可以分别设置每个标签对应一个数值；
比如：
       {好瓜→1坏瓜→0{ \ \ \ \ \ \ \ }\left\{\begin{array}{ll} 好瓜\rightarrow1 \\ 坏瓜\rightarrow0 \end{array}\right.       {好瓜→1坏瓜→0​

              {大→1大→0.5小→0{ \ \ \ \ \ \ { \ \ \ \ \ \ \ }\ }\left\{\begin{array}{ll} 大\rightarrow1 \\ 大\rightarrow0.5 \\ 小\rightarrow0 \end{array}\right.              ⎩⎨⎧​大→1大→0.5小→0​

对于变量值之间无法排序，也就是说各个属性值可能是并列的，比如颜色属性{绿色,黑色}与方向属性{东,南,西,北}；
如果属性有k个可能的取值，我们可以设置一个k维向量来表示属性值, 每个分量取值均为0或1代表是否是对应的属性值。
比如：绿色→\rightarrow→(1,0)
         {\ \ \ \ \ \ \ \ \ }          南方→\rightarrow→(0,1,0,0)
（ps：类似于经济学研究中虚拟变量的设置） 对数几率回归

回到西瓜的例子，我们现在已经将西瓜的标签{好瓜,坏瓜}设置成{0,1}。显然，这里的标签值就是线性模型中的yyy值，xxx则是西瓜的各种属性值。
如果将其带入基本模型f(x)=wTx+bf(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+bf(x)=wTx+b 之中，我们则会得到一个单位跃阶函数，如下图：
在wTx+b>0\boldsymbol{w}^T\boldsymbol{x}+b>0wTx+b>0时，y=1y=1y=1,
当wTx+b<0\boldsymbol{w}^T\boldsymbol{x}+b<0wTx+b<0时，y=0y=0y=0。

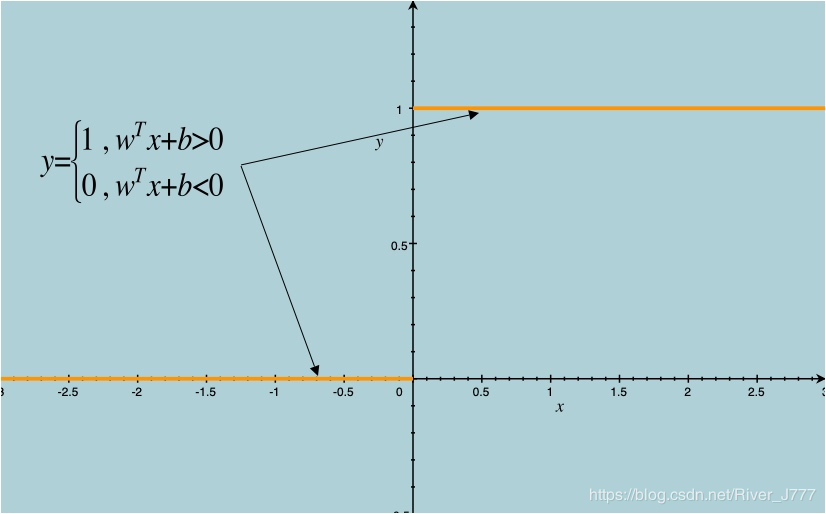
但是，跃阶函数并不是连续可微的，很难进行回归，于是数学家们找到了一个近似函数 ，称之为对数几率函数如图：

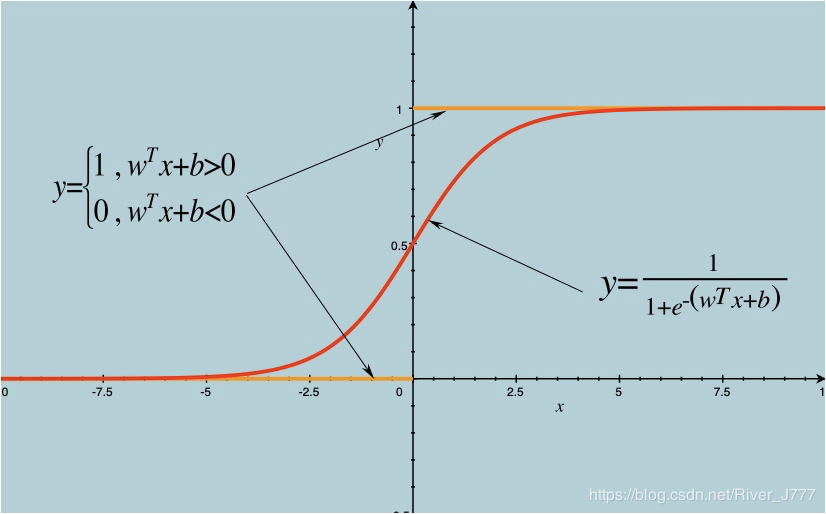
从图中我们可以看出，对数几率函数用来近似单位跃阶函数的两条极大的优点：

除了x=0附近，它可以把自变量转化成非常接近1或0的值； 它在x=0附近变化很陡。

凭借这两条优点，数学家们利用对数几率函数用来近似单位跃阶函数发明了对数几率回归，也叫做逻辑回归。（其实严格意义来说是分类方法，而不是回归方法）

对于wTx+b\boldsymbol{w}^{T} \boldsymbol{x}+bwTx+b，我们通常会在x\boldsymbol{x}x最后加入一列1作为常数项bbb的系数，记作x^\hat{\boldsymbol{x}}x^便可以将wTx+b\boldsymbol{w}^{T} \boldsymbol{x}+bwTx+b转化为βTx^\boldsymbol{\beta}^{T} \hat{\boldsymbol{x}}βTx^，以此来简化模型。
接着我们就可以用极大似然法对参数β\boldsymbol{\beta}β进行估计。
极大似然法的核心理念是“发生概率越大的事件越有可能发生”。所以我们要求出事件发生的概率，也就是在给定数据集后所有样本取到其对应标签的概率，定义为似然函数，并求最大值。不同的样本之间视为独立的，所以其联合事件的概率是各个样本概率的连乘，即：
ℓ(β)=∏i=1mp(yi∣x^i;β)\ell(\boldsymbol{\beta})=\prod_{i=1}^{m} p\left(y_{i} | \hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)ℓ(β)=i=1∏m​p(yi​∣x^i​;β)
取对数并不会改变似然函数的最大值点，所以为了方便计算，我们一般要取对数：
ℓ(β)=∑i=1mln⁡p(yi∣x^i;β) \ell(\boldsymbol{\beta})=\sum_{i=1}^{m} \ln p\left(y_{i} | \hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right) ℓ(β)=i=1∑m​lnp(yi​∣x^i​;β)

并可得标签取1或0的概率为：
p1(x^i;β)=eβTx^i1+eTx^i,p0(x^i;β)=11+eβTxip_1\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)=\frac{e^{\boldsymbol{\beta}^{T} }\hat{x}_{i}}{1+e^{\boldsymbol{T}}\hat{x}_{i}}, p_{0}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)=\frac{1}{1+e^{\boldsymbol{\beta}^{T} }\boldsymbol{x}_{i}} p1​(x^i​;β)=1+eTx^i​eβTx^i​​,p0​(x^i​;β)=1+eβTxi​1​

由于yi=0 or 1y_i=0\ or\ 1yi​=0 or 1, 则：
ℓ(β)={∑i=1m(−ln⁡(1+eβTx^i)),yi=0∑i=1m(βTx^i−ln⁡(1+eβTx^i)),yi=1 \ell(\boldsymbol{\beta})=\left\{\begin{array}{ll} \sum_{i=1}^{m}\left(-\ln \left(1+e^{\beta^{T} \hat{x}_{i}}\right)\right), & y_{i}=0 \\ \sum_{i=1}^{m}\left(\boldsymbol{\beta}^{T} \hat{\boldsymbol{x}}_{i}-\ln \left(1+e^{\boldsymbol{\beta}^{T} \hat{x}_{i}}\right)\right), & y_{i}=1 \end{array}\right. ℓ(β)=⎩⎨⎧​∑i=1m​(−ln(1+eβTx^i​)),∑i=1m​(βTx^i​−ln(1+eβTx^i​)),​yi​=0yi​=1​

整合成一个式子后并取相反数，我们可以知道，最大化似然函数等价于最小化下式：
ℓ(β)=∑i=1m(−yiβTx^i+ln⁡(1+eβTx^i)) \ell(\boldsymbol{\beta})=\sum_{i=1}^{m}\left(-y_{i} \boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_{i}+\ln \left(1+e^{\boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_{i}}\right)\right) ℓ(β)=i=1∑m​(−yi​βTx^i​+ln(1+eβTx^i​))
并求对应的参数β\boldsymbol{\beta}β，即：
β∗=arg⁡min⁡βℓ(β) \boldsymbol{\beta}^{*}=\underset{\boldsymbol{\beta}}{\arg \min } \ell(\boldsymbol{\beta}) β∗=βargmin​ℓ(β)
对于如同本文中似然函数的高阶可导连续凸函数，根据凸优化理论，可以利用最速下降法、牛顿法等求其最值。
以牛顿法为例, 其第 t + 1 轮迭代解的更新公式为：
βt+1=βt−(∂2ℓ(β)∂β∂βT)−1∂ℓ(β)∂β \boldsymbol{\beta}^{t+1}=\boldsymbol{\beta}^{t}-\left(\frac{\partial^{2} \ell(\boldsymbol{\beta})}{\partial \boldsymbol{\beta} \partial \boldsymbol{\beta}^{\mathrm{T}}}\right)^{-1} \frac{\partial \ell(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} βt+1=βt−(∂β∂βT∂2ℓ(β)​)−1∂β∂ℓ(β)​
可以表示为：

{βk+1=βk+dkdk=−(∂2ℓ(β)∂β∂βT)−1∂ℓ(β)∂β \left\{ \begin{aligned} &\boldsymbol{\beta}^{k+1}=\boldsymbol{\beta}^{k}+\boldsymbol{d}^k \\ &\boldsymbol{d}^k=-\left(\frac{\partial^{2} \ell(\boldsymbol{\beta})}{\partial \boldsymbol{\beta} \partial \boldsymbol{\beta}^{\mathrm{T}}}\right)^{-1} \frac{\partial \ell(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} \end{aligned} \right. ⎩⎪⎨⎪⎧​​βk+1=βk+dkdk=−(∂β∂βT∂2ℓ(β)​)−1∂β∂ℓ(β)​​
其中，dk\boldsymbol{d}^kdk称为牛顿方向.

牛顿法等算法推导过程见我的另外一篇博客，戳此处～

式子中关于β\boldsymbol{\beta}β的一阶、二阶导数为：
∂ℓ(β)∂β=−∑i=1mx^i(yi−p1(x^i;β))∂2ℓ(β)∂β∂βT=∑i=1mx^ix^iTp1(x^i;β)(1−p1(x^i;β)) \begin{aligned} \frac{\partial \ell(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} &=-\sum_{i=1}^{m} \hat{\boldsymbol{x}}_{i}\left(y_{i}-p_{1}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)\right) \\ \frac{\partial^{2} \ell(\boldsymbol{\beta})}{\partial \boldsymbol{\beta} \partial \boldsymbol{\beta}^{\mathrm{T}}} &=\sum_{i=1}^{m} \hat{\boldsymbol{x}}_{i} \hat{\boldsymbol{x}}_{i}^{\mathrm{T}} p_{1}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)\left(1-p_{1}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)\right) \end{aligned}∂β∂ℓ(β)​∂β∂βT∂2ℓ(β)​​=−i=1∑m​x^i​(yi​−p1​(x^i​;β))=i=1∑m​x^i​x^iT​p1​(x^i​;β)(1−p1​(x^i​;β))​
所以算法的流程为：

给定待估参数β\boldsymbol{\beta}β的初始值β0\boldsymbol{\beta}_0β0​，给定允许误差ϵ>0\epsilon>0ϵ>0，置迭代次数n=0n=0n=0； 计算牛顿方向dk=−(∂2ℓ(β)∂β∂βT)−1∂ℓ(β)∂β\boldsymbol{d}^k=-\left(\frac{\partial^{2} \ell(\boldsymbol{\beta})}{\partial \boldsymbol{\beta} \partial \boldsymbol{\beta}^{\mathrm{T}}}\right)^{-1} \frac{\partial \ell(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}}dk=−(∂β∂βT∂2ℓ(β)​)−1∂β∂ℓ(β)​； 如果∥dk∥<ϵ\| \textbf{d}_k\|<\epsilon∥dk​∥<ϵ，则停止运算；
否则，更新βk+1=βk+dk\boldsymbol{\beta}^{k+1}=\boldsymbol{\beta}^{k}+\boldsymbol{d}^kβk+1=βk+dk，置n=n+1n=n+1n=n+1,转到步骤2；

于是，我们便可以利用对数几率函数进行回归，称之为对数几率回归，以课后习题3.3为例。

课后习题3.3

3.3 编程实现对率回归，并给出西瓜数据集3.0α\alphaα上的结果。
数据集：西瓜数据集3.0α\alphaα 提取码:950l
首先，我们要读取数据集，并将样本属性与标签分别存入xxx、yyy中：

# 读取数据 inputfile = '/Users/Downloads/test.xlsx' data_original = pd.read_excel(inputfile) # 为了方便运算一般将x矩阵转置，得到2行17列的矩阵，第一行为密度，第二行为含糖率；加入一行1作为第三行，对应于常数项b x = np.array( [list(data_original[u'密度']), list(data_original[u'含糖率']), [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]) y = np.array([1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0])

其次，我们要初始化参数。
牛顿法等数值算法估计β\boldsymbol{\beta}β均需要迭代计算，所以需要定义初始值，即密度的系数、含糖率的系数和常数项bbb，此处初始值设为0，0，1.
允许误差epsilonepsilonepsilon，设为0.00001.
另外定义nnn记录迭代次数，初始值为0.

# 定义初始值,分别对应密度、含糖率与常数项的系数 beta = np.array([[0], [0], [1]]) # β列向量 n = 0 epsilon = 0.000001

开始牛顿法的迭代，使用while循环，跳出循环条件在后面

while 1:

为了便于计算似然函数关于β\boldsymbol{\beta}β的导数，现将β\boldsymbol{\beta}β与x\boldsymbol{x}x的乘积记为一个整体，记作beta_xbeta\_xbeta_x.

# 对β进行转置取第一行，再与x相乘（dot）,beta_x表示β转置乘以x beta_x = np.dot(beta.T[0], x)

通过先求出关于β\boldsymbol{\beta}β的一阶、二阶导数来求出牛顿方向d

# 先求关于β的一阶导数和二阶导数 dbeta = 0 d2beta = 0 for i in range(17): # 一阶导数 dbeta = dbeta - np.dot(np.array([x[:, i]]).T, (y[i] - (np.exp(beta_x[i]) / (1 + np.exp(beta_x[i]))))) # 二阶导数 d2beta = d2beta + np.dot(np.array([x[:, i]]).T, np.array([x[:, i]]).T.T) * ( np.exp(beta_x[i]) / (1 + np.exp(beta_x[i]))) * ( 1 - (np.exp(beta_x[i]) / (1 + np.exp(beta_x[i])))) #得到牛顿方向 d = - np.dot(linalg.inv(d2beta), dbeta)

根据牛顿方向的模与事先给定的允许误差ϵ\epsilonϵ比较大小，如果小于允许误差，则认为很接近极小值点，停止迭代：

# 迭代终止条件 if np.linalg.norm(d) <= epsilon: # 牛顿方向向量的模小于0.000001时认为很接近极小值点，停止迭代 break # 满足条件直接跳出循环

如果大于允许误差ϵ\epsilonϵ，则更新待估参数β\boldsymbol{\beta}β,继续迭代

# 牛顿迭代法更新β beta = beta + d n = n + 1

输出结果：

print('模型参数：') print(' 密度的系数为: ',beta[0],'\n','含糖率的系数为:',beta[1],'\n','常数项为: ',beta[2]) print('迭代次数：', n)

全部代码为：

# 对率回归分类 import numpy as np from numpy import linalg import pandas as pd # 读取数据 inputfile = '/Users/Downloads/test.xlsx' data_original = pd.read_excel(inputfile) # 为了方便运算一般将x矩阵转置，得到2行17列的矩阵，第一行为密度，第二行为含糖率；加入一行1作为第三行，对应于常数项b x = np.array( [list(data_original[u'密度']), list(data_original[u'含糖率']), [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]) y = np.array([1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]) # 定义初始值,分别对应密度、含糖率与常数项的系数 beta = np.array([[0], [0], [1]]) # β列向量 n = 0 epsilon = 0.000001 while 1: # 对β进行转置取第一行 # 再与x相乘（dot）,beta_x表示β转置乘以x) beta_x = np.dot(beta.T[0], x) # 先求关于β的一阶导数和二阶导数 dbeta = 0 d2beta = 0 for i in range(17): # 一阶导数 dbeta = dbeta - np.dot(np.array([x[:, i]]).T, (y[i] - (np.exp(beta_x[i]) / (1 + np.exp(beta_x[i]))))) # 二阶导数 d2beta = d2beta + np.dot(np.array([x[:, i]]).T, np.array([x[:, i]]).T.T) * ( np.exp(beta_x[i]) / (1 + np.exp(beta_x[i]))) * ( 1 - (np.exp(beta_x[i]) / (1 + np.exp(beta_x[i])))) #得到牛顿方向 d = - np.dot(linalg.inv(d2beta), dbeta) # 迭代终止条件 if np.linalg.norm(d) <= epsilon: # 牛顿方向向量的模小于0.000001时认为很接近极小值点，停止迭代 break # 满足条件直接跳出循环 # 牛顿迭代法更新β beta = beta + d n = n + 1 print('模型参数：') print(' 密度的系数为: ',beta[0],'\n','含糖率的系数为:',beta[1],'\n','常数项为: ',beta[2]) print('迭代次数：', n)

结果为：

模型参数： 密度的系数为: [3.15832966] 含糖率的系数为: [12.52119579] 常数项为: [-4.42886451] 迭代次数： 5

第三章的学习笔记很详细地将对数几率回归算法的来历、原理与编程展现给了大家，本章的其他内容如Fisher判别分析等，以理解算法的思维为主，大家阅读书本即可。

相关链接：
周志华《机器学习》西瓜书 小白Python学习笔记（一） ———— 第一章 绪论 & 第二章 模型评估与选择

作者：River_J777

周志华 python学习 对数几率 学习 回归 几率 模型 线性模型 线性 对数 机器学习 Python