通过python程序,采用牛顿法和梯度下降法求解多元一次函数的线性回归方程
通过python程序,采用牛顿法和梯度下降法求解多元一次函数的线性回归方程
梯度下降法原理
作者:是陆小鹿啊
梯度就是表示某一函数在该点处的方向导数沿着该方向取得较大值,即函数在当前位置的导数
Δ=df(Ɵ)÷d(Ɵ)
上式中,Ɵ是自变量,f(Ɵ)是关于Ɵ的函数,Ɵ表示梯度 简单来说Δ就是函数相对于自变量Ɵ的求导
梯度下降算法公式: Ɵ=Ɵ0-Ƞ*Δf(Ɵ0)
其中Ƞ是学习因子,由我们自己定义,Ɵ即为数据更新后下一个Ɵ0
f(Ɵ)=f(Ɵ0)+(Ɵ-Ɵ0)*Δf(Ɵ0)
通过该公示不断地进行数据迭代,就可以得到最终的数据
梯度下降法求解二元一次线性回归方程import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
data=np.genfromtxt('C:\\Users\\ll\\Desktop\\作业六2题.csv',delimiter=',') #导入数据
x_data=data[:,:-1]
y_data=data[:,2]
#定义学习率、斜率、截据a
#设方程为y=theta1x1+theta2x2+theta0
lr=0.00001
theta0=0
theta1=0
theta2=0
#定义最大迭代次数,因为梯度下降法是在不断迭代更新k与b
epochs=10000
#定义最小二乘法函数-损失函数(代价函数)
def compute_error(theta0,theta1,theta2,x_data,y_data):
totalerror=0
for i in range(0,len(x_data)):#定义一共有多少样本点
totalerror=totalerror+(y_data[i]-(theta1*x_data[i,0]+theta2*x_data[i,1]+theta0))**2
return totalerror/float(len(x_data))/2
#梯度下降算法求解参数
def gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs):
m=len(x_data)
for i in range(epochs):
theta0_grad=0
theta1_grad=0
theta2_grad=0
for j in range(0,m):
theta0_grad-=(1/m)*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta2)+y_data[j])
theta1_grad-=(1/m)*x_data[j,0]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
theta2_grad-=(1/m)*x_data[j,1]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
theta0=theta0-lr*theta0_grad
theta1=theta1-lr*theta1_grad
theta2=theta2-lr*theta2_grad
return theta0,theta1,theta2
#进行迭代求解
theta0,theta1,theta2=gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs)
print('结果:')
print('迭代次数:{0} 学习率:{1} a0={2},a1={3},a2={4},代价函数为{5}'.format(epochs,lr,theta0,theta1,theta2,compute_error(theta0,theta1,theta2,x_data,y_data)))
print("多元线性回归方程为:y=",theta1,"X1",theta2,"X2+",theta0)
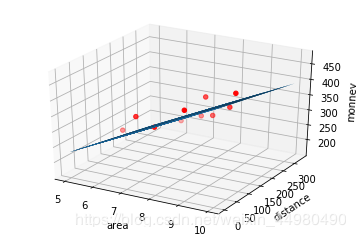
#画图
ax=plt.figure().add_subplot(111,projection='3d')
ax.scatter(x_data[:,0],x_data[:,1],y_data,c='r',marker='o')
x0=x_data[:,0]
x1=x_data[:,1]
#生成网格矩阵
x0,x1=np.meshgrid(x0,x1)
z=theta0+theta1*x0+theta2*x1
#画3d图
ax.plot_surface(x0,x1,z)
ax.set_xlabel('area')
ax.set_ylabel('distance')
ax.set_zlabel("monney")
plt.show()
结果:
迭代次数:10000 学习率:1e-05 a0=5.3774162274868,a1=45.0533119768975,a2=-0.19626929358281256,代价函数为366.7314528822914
多元线性回归方程为:y= 45.0533119768975 X1 -0.19626929358281256 X2+ 5.3774162274868
牛顿法的基本思想是利用迭代点 x_{k} 处的一阶导数 (梯度)和二阶导数 ( Hessen 矩阵) 对目标函数进行二次函数近似,然后把二次模型的极小点作为新的迭代点,并不断重复这一过程,直至求得满足精度的近似极小值。牛顿法的速度相当快,而且能高度逼近最优值。
牛顿法迭代公式:
X(k+1)=X(k)-F(Xk)/F'(Xk)
#导入相关库及数据文件
import pandas as pd
import numpy as np
from numpy import array
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import math
d= pd.read_excel('C:\\Users\\ll\\Desktop\\作业六2题.xlsx')
#根据表头名称定义参数
x1=d['店铺面积']
x2=d['车站距离']
y=d['月营业额(万日元)']
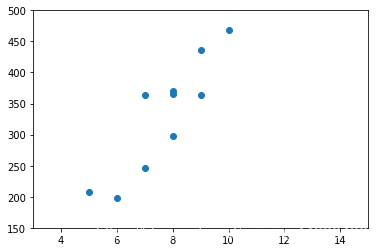
#月营业额与店铺面积的回归关系
plt.scatter(x1,y)
plt.axis([3,15,150,500])
plt.show()
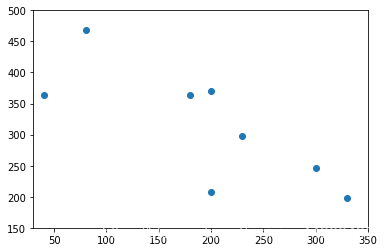
#月营业额与距离车站距离的回归关系
plt.scatter(x2,y)
plt.axis([30,350,150,500])
plt.show()
data = np.genfromtxt("C:\\Users\\ll\\Desktop\\作业六2题.csv",delimiter=",")
x1=data[0:10,0]#店铺面积
x2=data[0:10,1]#车站距离
y=data[0:10,2]#月营业额
#月营业额矩阵化
y1=np.array([y]).T
#为自变量系数矩阵X赋值
x11=np.array([x1]).T
x22=np.array([x2]).T
#创建系数矩阵
A=np.array([[1],[1],[1],[1],[1],[1],[1],[1],[1],[1]])
#将矩阵A与矩阵X11合并为矩阵B
B=np.hstack((A,x11))
#将矩阵B与矩阵X22合并为矩阵C
C=np.hstack((B,x22))
#矩阵C的转置矩阵
C_=C.T
C_
array([[ 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[ 10., 8., 8., 5., 7., 8., 7., 9., 6., 9.],
[ 80., 0., 200., 200., 300., 230., 40., 0., 330., 180.]])
#矩阵C的转置矩阵与矩阵C的乘积
C_C=np.dot(C_,C)
C_C
array([[1.000e+01, 7.700e+01, 1.560e+03],
[7.700e+01, 6.130e+02, 1.122e+04],
[1.560e+03, 1.122e+04, 3.722e+05]])
#求矩阵C与他的转置矩阵的C_的乘积的逆矩阵
C_C_=np.linalg.inv(C_C)
#求解系数矩阵w
w=np.dot(np.dot((C_C_),(C_)),y1)
w
array([[65.32391639],
[41.51347826],
[-0.34088269]])
b=w[0][0]
a1=w[1][0]
a2=w[2][0]
print("系数a1=",a1)
print("系数a2=",a2)
print("截距为=",b)
print("多元线性回归方程为:y=",a1,"x1+(",a2,")x2+",b)
系数a1= 41.51347825643848
系数a2= -0.34088268566362023
截距为= 65.32391638894899
多元线性回归方程为:y= 41.51347825643848 x1+( -0.34088268566362023 )x2+ 65.32391638894899
三、牛顿法和梯度下降法的比较
1.牛顿法:是通过求解目标函数的一阶导数为0时的参数,进而求出目标函数最小值时的参数。
优点:收敛速度很快。矩阵的逆在迭代过程中不断减小,可以起到逐步减小步长的效果。
缺点:矩阵的逆计算复杂,代价比较大
2.梯度下降法:是通过梯度方向和步长,直接求解目标函数的最小值时的参数。
越接近最优值时,步长应该不断减小,否则会在最优值附近来回震荡。
作者:是陆小鹿啊