Python实现多元线性回归方程梯度下降法与求函数极值

Vivienne ·

更新时间:2024-09-21

· 781 次阅读

梯度下降法

梯度下降法的基本思想可以类比为一个下山的过程。
假设这样一个场景：一个人被困在山上，需要从山上下来(找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低；因此，下山的路径就无法确定，必须利用自己周围的信息一步一步地找到下山的路。这个时候，便可利用梯度下降算法来帮助自己下山。怎么做呢，首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处；同理上山也是如此，只是这时候就变成梯度上升算法了
在这里插入图片描述
梯度下降

梯度下降的基本过程就和下山的场景很类似。

首先，我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值，也就是山底。根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对应到函数中，就是找到给定点的梯度，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数之变化最快的方向(在后面会详细解释)
所以，我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向，也就是场景中测量方向的手段。

牛顿法

并不是所有的方程都有求根公式，或者求根公式很复杂，导致求解困难。利用牛顿法，可以迭代求解。

原理是利用泰勒公式，在x0处展开，且展开到一阶，即f(x) = f(x0)+(x－x0)f’(x0)

求解方程f(x)=0，即f(x0)+(x-x0)f’(x0)=0，求解x = x1=x0－f(x0)/f’(x0)，因为这是利用泰勒公式的一阶展开，f(x) = f(x0)+(x－x0)f’(x0)处并不是完全相等，而是近似相等，这里求得的x1并不能让f（x）=0，只能说f(x1)的值比f(x0)更接近f（x）=0，于是乎，迭代求解的想法就很自然了，可以进而推出x(n+1)=x(n)－f(x(n))/f’(x(n))，通过迭代，这个式子必然在f（x）=0的时候收敛。整个过程如下图：
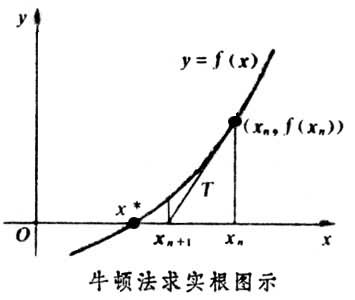
在这里插入图片描述
从本质上去看，牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。（牛顿法目光更加长远，所以少走弯路；相对而言，梯度下降法只考虑了局部的最优，没有全局思想。）

根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

用 Python编程，完成函数极值的求解

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
from mpl_toolkits.mplot3d import Axes3D
import warnings

def f2(x1,x2):
    return x1*x1+2*x2*x2-4*x1-2*x1*x2
X1 = np.arange(-4,4,0.2)
X2 = np.arange(-4,4,0.2)
X1, X2 = np.meshgrid(X1, X2) # 生成xv、yv，将X1、X2变成n*m的矩阵，方便后面绘图
Y = np.array(list(map(lambda t : f2(t[0],t[1]),zip(X1.flatten(),X2.flatten()))))
Y.shape = X1.shape # 1600的Y图还原成原来的（40,40）
%matplotlib inline
#作图
fig = plt.figure(facecolor='w')
ax = Axes3D(fig)
ax.plot_surface(X1,X2,Y,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.set_title(u'$ y = x1^2+2x2^2-4x1-2x1x2 $')
plt.show()

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
def Fun(x,y):#原函数
    return x-y+2*x*x+2*x*y+y*y
def PxFun(x,y):#偏x导
    return 1+4*x+2*y
def PyFun(x,y):#偏y导
    return -1+2*x+2*y
#初始化
fig=plt.figure()#figure对象
ax=Axes3D(fig)#Axes3D对象
X,Y=np.mgrid[-2:2:40j,-2:2:40j]#取样并作满射联合
Z=Fun(X,Y)#取样点Z坐标打表
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap="rainbow")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
#梯度下降
step=0.0008#下降系数
x=0
y=0#初始选取一个点
tag_x=[x]
tag_y=[y]
tag_z=[Fun(x,y)]#三个坐标分别打入表中，该表用于绘制点
new_x=x
new_y=y
Over=False
while Over==False:
    new_x-=step*PxFun(x,y)
    new_y-=step*PyFun(x,y)#分别作梯度下降
    if Fun(x,y)-Fun(new_x,new_y)<7e-9:#精度
        Over=True
    x=new_x
    y=new_y#更新旧点
    tag_x.append(x)
    tag_y.append(y)
    tag_z.append(Fun(x,y))#新点三个坐标打入表中
#绘制点/输出坐标
ax.plot(tag_x,tag_y,tag_z,'r.')
plt.title('(x,y)~('+str(x)+","+str(y)+')')
plt.show()

用 Python编程，完成梯度下降法

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
data=np.genfromtxt('D:/作业/人工实验6.csv',delimiter=',')
x_data=data[:,:-1]
y_data=data[:,2]
#定义学习率、斜率、截据
#设方程为y=theta1x1+theta2x2+theta0
lr=0.00001
theta0=0
theta1=0
theta2=0
#定义最大迭代次数，因为梯度下降法是在不断迭代更新k与b
epochs=10000
#定义最小二乘法函数-损失函数（代价函数）
def compute_error(theta0,theta1,theta2,x_data,y_data):
    totalerror=0
    for i in range(0,len(x_data)):#定义一共有多少样本点
        totalerror=totalerror+(y_data[i]-(theta1*x_data[i,0]+theta2*x_data[i,1]+theta0))**2
    return totalerror/float(len(x_data))/2
#梯度下降算法求解参数
def gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs):
    m=len(x_data)
    for i in range(epochs):
        theta0_grad=0
        theta1_grad=0
        theta2_grad=0
        for j in range(0,m):
            theta0_grad-=(1/m)*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta2)+y_data[j])
            theta1_grad-=(1/m)*x_data[j,0]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
            theta2_grad-=(1/m)*x_data[j,1]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
        theta0=theta0-lr*theta0_grad
        theta1=theta1-lr*theta1_grad
        theta2=theta2-lr*theta2_grad
    return theta0,theta1,theta2
#进行迭代求解
theta0,theta1,theta2=gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs)
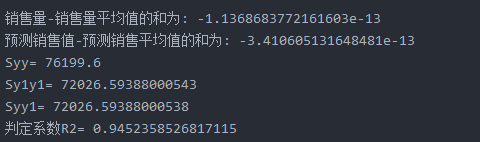
print('结果：迭代次数：{0} 学习率：{1}之后 a0={2},a1={3},a2={4},代价函数为{5}'.format(epochs,lr,theta0,theta1,theta2,compute_error(theta0,theta1,theta2,x_data,y_data)))
print("多元线性回归方程为:y=",theta1,"X1+",theta2,"X2+",theta0)
#画图
ax=plt.figure().add_subplot(111,projection='3d')
ax.scatter(x_data[:,0],x_data[:,1],y_data,c='r',marker='o')
x0=x_data[:,0]
x1=x_data[:,1]
#生成网格矩阵
x0,x1=np.meshgrid(x0,x1)
z=theta0+theta1*x0+theta2*x1
#画3d图
ax.plot_surface(x0,x1,z)
ax.set_xlabel('area')
ax.set_ylabel('distance')
ax.set_zlabel("Monthly turnover")
plt.show()

在这里插入图片描述