吴恩达机器学习课程CODE1:线性回归算法(应用平方误差与梯度下降)
线性回归问题需要有一个真实的直线来对给定x求出y,但现在我们不知道这条直线,需要根据训练集去拟合一条无限逼近这条真实直线的直线,以用于预测。
如图根据训练集,力求得到一条可以拟合尽量多点的直线:
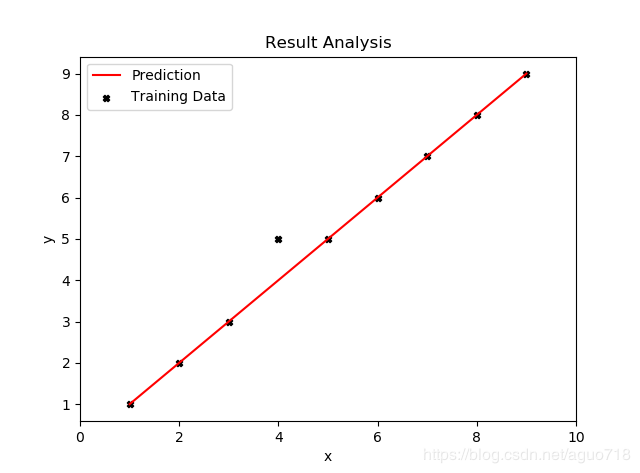
假设函数:hθ(x(i))=θ0+θ1xh_\theta (x^{(i)})=\theta _0+\theta _1xhθ(x(i))=θ0+θ1x
θ0,θ1\theta _0, \theta _1θ0,θ1是其的两个参数,即待求的两个参数
代价函数(损失函数):J(θ0,θ1)=12m∑i=1m(hθ(x(i))−y(i))2J(θ_0,θ_1)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta (x^{(i)})-y^{(i)})^2J(θ0,θ1)=2m1∑i=1m(hθ(x(i))−y(i))2
应用平方误差代价函数(Squared error function --解决回归问题常用的手段)
目标: minimizeθ0,θ1J(θ0,θ1)minimize_{θ_0,θ_1}J(θ_0,θ_1)minimizeθ0,θ1J(θ0,θ1) ------最小化损失函数J
3)梯度下降最小化损失函数可应用梯度下降算法解决。
取某一个参数如θ1\theta _1θ1,把损失函数看做J(θ1)J(\theta_1)J(θ1),则该曲线如图:
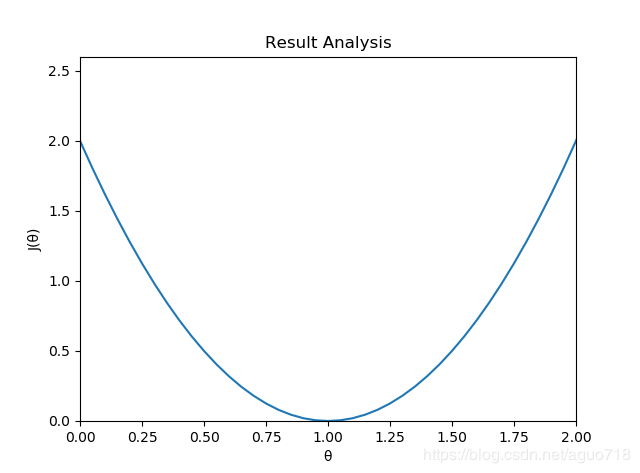
根据梯度下降算法使结果收敛到(1,0)点(当前点在该点左边则θ\thetaθ加上某个值,小步向J(θ)J(\theta)J(θ)最小点(1,0)靠近;当前点在该点右边则θ\thetaθ减去某个值,小步向J(θ)J(\theta)J(θ)最小点(1,0)靠近)
即θ=0\theta =0θ=0时,J(θ)J(\theta)J(θ)取最小值,即实现目标,此θ=1\theta=1θ=1即为所求。
梯度下降算法描述如下:
repeat util convergence{repeat\ util\ convergence\{repeat util convergence{
θj:=θj−α∂∂θjJ(θ0,θ1)\ \ \ \ \ \ \ \ \ \ \ \theta_j :=\theta_j-\alpha\frac{\partial}{\partial \theta_j}J(\theta_0, \theta_1) θj:=θj−α∂θj∂J(θ0,θ1)
(for j=0 and j=1)\
\ \ \ \ \ \ \ \ \ \ (for\ j=0\ and\ j=1) (for j=0 and j=1)
}\}}
将上一部分的J(θ0,θ1)J(θ_0,θ_1)J(θ0,θ1)代入,求偏导该梯度下降可写为:
repeat util convergence{repeat\ util\ convergence\{repeat util convergence{
θ0:=θ0−α1m∑i=1m(hθ(x(i))−y(i))\ \ \ \ \ \ \ \ \ \ \ \theta_0 :=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)}) θ0:=θ0−αm1∑i=1m(hθ(x(i))−y(i))
θ1:=θ1−α1m∑i=1m(hθ(x(i))−y(i))⋅x(i)\ \ \ \ \ \ \ \ \ \ \ \theta_1 :=\theta_1-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})\cdot x^{(i)} θ1:=θ1−αm1∑i=1m(hθ(x(i))−y(i))⋅x(i)
}\}}
(下一部分代码实现主要应用这两个公式,使1m∑i=1m(hθ(x(i))−y(i))\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})m1∑i=1m(hθ(x(i))−y(i))无限趋近于0作为循环终止条件,即J(θ)J(\theta)J(θ)导数值趋近于0、θ\thetaθ的变化极小)
注: 所有参数同步更新(simultaneous update ------梯度下降中一种最常用的方法),即
temp0:=θ0−α∂∂θ0J(θ0,θ1)temp0 :=\theta_0-\alpha\frac{\partial}{\partial \theta_0}J(\theta_0, \theta_1)temp0:=θ0−α∂θ0∂J(θ0,θ1)
temp1:=θ1−α∂∂θ1J(θ0,θ1)temp1 :=\theta_1-\alpha\frac{\partial}{\partial \theta_1}J(\theta_0, \theta_1)temp1:=θ1−α∂θ1∂J(θ0,θ1)
θ0=temp0\theta_0=temp0θ0=temp0
θ1=temp1\theta_1=temp1θ1=temp1
import pandas as pd
import numpy as np
dataset = pd.read_csv('./datasetsxy.csv')
col = dataset.columns.values.tolist() # 把每一列转换成一个list
datax = np.array(dataset[col[0]])
datay = np.array(dataset[col[1]])
m = len(datax) # the number of samples
a = 0.001 # 学习率初始化为0.001
b0 = 0
b1 = 1
while (1):
# 此处为梯度下降算法
sum0 = 0
sum1 = 0
for i in range(m):
sum0 = sum0 + (b0 + b1 * datax[i] - datay[i])
sum1 = sum1 + (b0 + b1 * datax[i] - datay[i]) * datax[i]
Jsum0 = (1 / m) * sum0 # J(θ)的导数
Jsum1 = (1 / m) * sum1
c0 = (Jsum0 < 0.001) # 导数接近0时,也可以理解为循环到θ值变化很小时
c1 = (Jsum1 < 0.001)
if c0 & c1:
break
b0 = b0 - a * Jsum0
b1 = b1 - a * Jsum1
print('y = ' ,b1 ,'x+', b0)
2)点和线(第一部分第一个图)
dataset = pd.read_csv('./datasetsxy.csv')
col = dataset.columns.values.tolist()
datax = np.array(dataset[col[0]])
datay = np.array(dataset[col[1]])
plt.ion()
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
ax1.set_title('Result Analysis')
ax1.set_xlabel('x')
ax1.set_ylabel('y')
plt.xlim(xmax=10, xmin=0)
ax1.scatter(datax, datay, s=20, c='k', marker='X', label='Training Data') # 画点
ax1.plot(datax, datax, 'r', label='Prediction') # 画线
ax1.legend(loc=2) # 标注点线等的含义
plt.show()
plt.waitforbuttonpress()
3)二次曲线(第一部分第二个图)
plt.ion()
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
ax1.set_title('Result Analysis')
ax1.set_xlabel('θ')
ax1.set_ylabel('J(θ)')
plt.xlim(xmax=2, xmin=0)
plt.ylim(ymax=2.6, ymin=0)
x = np.arange(0, 3, 0.05)
ax1.plot(x, 2*x*x-4*x+2)
plt.show()
plt.waitforbuttonpress()
欢迎讨论>_<
作者:aguo718