机器学习——从线性回归到逻辑回归【附详细推导和代码】

Nimat ·

更新时间:2024-09-21

· 736 次阅读

本文始发于个人公众号：TechFlow，原创不易，求个关注

在之前的文章当中，我们推导了线性回归的公式，线性回归本质是线性函数，模型的原理不难，核心是求解模型参数的过程。通过对线性回归的推导和学习，我们基本上了解了机器学习模型学习的过程，这是机器学习的精髓，要比单个模型的原理重要得多。

新关注和有所遗忘的同学可以点击下方的链接回顾一下之前的线性回归和梯度下降的内容。

一文讲透梯度下降法

详细推导线性回归模型

回归与分类

在机器学习当中，模型根据预测结果的不同分为两类，如果我们希望模型预测一个或者多个连续值，这类问题被称为是回归问题。像是常见的未来股票价格的估计、未来温度估计等等都算是回归问题。还有一类呢是分类问题，模型的预测结果是一个离散值，也就是说只有固定的种类的结果。常见的有垃圾邮件识别、网页图片鉴黄等等。

我们之前介绍的逻辑回归顾名思义是一个回归问题，今天的文章讲的呢是如何将这个回归模型转化成分类模型，这个由线性回归推导得到的分类模型称为逻辑回归。

逻辑回归

逻辑回归这个模型很神奇，虽然它的本质也是回归，但是它是一个分类模型，并且它的名字当中又包含”回归“两个字，未免让人觉得莫名其妙。

如果是初学者，觉得头晕是正常的，没关系，让我们一点点捋清楚。

让我们先回到线性回归，我们都知道，线性回归当中y=WX+by=WX+by=WX+b。我们通过W和b可以求出X对应的y，这里的y是一个连续值，是回归模型对吧。但如果我们希望这个模型来做分类呢，应该怎么办？很容易想到，我们可以人为地设置阈值对吧，比如我们规定y > 0最后的分类是1，y < 0最后的分类是0。从表面上来看，这当然是可以的，但实际上这样操作会有很多问题。

最大的问题在于如果我们简单地设计一个阈值来做判断，那么会导致最后的y是一个分段函数，而分段函数不连续，使得我们没有办法对它求梯度，为了解决这个问题，我们得找到一个平滑的函数使得既可以用来做分类，又可以解决梯度的问题。

很快，信息学家们找到了这样一个函数，它就是Sigmoid函数，它的表达式是：

σ(x)=11+e−x\sigma(x)= \frac{1}{1+e^{-x}}σ(x)=1+e−x1

它的函数图像如下：

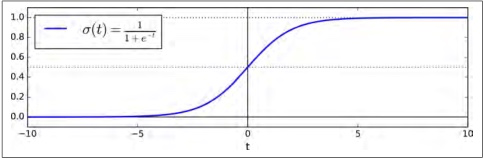
可以看到，sigmoid函数在x=0处取值0.5，在正无穷处极限是1，在负无穷处极限是0，并且函数连续，处处可导。sigmoid的函数值的取值范围是0-1，非常适合用来反映一个事物发生的概率。我们认为σ(x)\sigma(x)σ(x)表示x发生的概率，那么x不发生的概率就是1−σ(x)1-\sigma(x)1−σ(x)。我们把发生和不发生看成是两个类别，那么sigmoid函数就转化成了分类函数，如果σ(x)>0.5\sigma(x)>0.5σ(x)>0.5表示类别1，否则表示类别0.

到这里就很简单了，通过线性回归我们可以得到y=WX+b,P(1)=σ(y),P(0)=1−σ(y)y = WX + b, P(1)=\sigma(y), P(0)=1-\sigma(y)y=WX+b,P(1)=σ(y),P(0)=1−σ(y)。也就是说我们在线性回归模型的外面套了一层sigmoid函数，我们通过计算出不同的y，从而获得不同的概率，最后得到不同的分类结果。

损失函数

下面的推导全程高能，我相信你们看完会三连的（点赞、转发、关注）。

让我们开始吧，我们先来确定一下符号，为了区分，我们把训练样本当中的真实分类命名为yyy，yyy的矩阵写成YYY。同样，单条样本写成xxx,xxx的矩阵写成XXX。单条预测的结果写成y^\hat{y}y^，所有的预测结果写成Y^\hat{Y}Y^。

对于单条样本来说，y有两个取值，可能是1，也可能是0，1和0代表两个不同的分类。我们希望y=1y = 1y=1的时候，y^\hat{y}y^尽量大，y=0y = 0y=0时，1−y^1 - \hat{y}1−y^尽量大，也就是y^\hat{y}y^尽量小，因为它取值在0-1之间。我们用一个式子来统一这两种情况：

P(y∣x)=y^y(1−y^)1−yP(y|x)=\hat{y}^y(1-\hat{y})^{1-y}P(y∣x)=y^y(1−y^)1−y

我们代入一下，y=0y=0y=0时前项为1，表达式就只剩下后项，同理，y=1y=1y=1时，后项为1，只剩下前项。所以这个式子就可以表示预测准确的概率，我们希望这个概率尽量大。显然，P(y∣x)>0P(y|x)>0P(y∣x)>0，所以我们可以对它求对数，因为log函数是单调的。所以P(y∣x)P(y|x)P(y∣x)取最值时的取值，就是logP(y∣x)logP(y|x)logP(y∣x)取最值的取值。

log⁡P(y∣x)=ylog⁡y^+(1−y)log⁡(1−y^)\log P(y|x)=y\log \hat{y} + (1-y)\log (1-\hat{y})logP(y∣x)=ylogy^+(1−y)log(1−y^)

我们期望这个值最大，也就是期望它的相反数最小，我们令J=−log⁡P(y∣x)J=-\log P(y|x)J=−logP(y∣x)，这样就得到了它的损失函数：

J(θ)=−1mYlog⁡Y^+(1−Y)log⁡(1−Y^)J(\theta)=-\frac{1}{m}Y\log \hat{Y} + (1-Y)\log (1-\hat{Y})J(θ)=−m1YlogY^+(1−Y)log(1−Y^)

如果知道交叉熵这个概念的同学，会发现这个损失函数的表达式其实就是交叉熵。交叉熵是用来衡量两个概率分布之间的”距离“，交叉熵越小说明两个概率分布越接近，所以经常被用来当做分类模型的损失函数。关于交叉熵的概念我们这里不多赘述，会在之后文章当中详细介绍。我们随手推导的损失函数刚好就是交叉熵，这并不是巧合，其实底层是有一套信息论的数学逻辑支撑的，我们不多做延伸，感兴趣的同学可以了解一下。

硬核推导

损失函数有了，接下来就是求梯度来实现梯度下降了。

这个函数看起来非常复杂，要对它直接求偏导过于硬核（危），如果是许久不碰高数的同学直接肝不亚于硬抗苇名一心。

为了简化难度，我们先来做一些准备工作。首先，我们先来看下σ\sigmaσ函数，它本身的形式很复杂，我们先把它的导数搞定。

(11+e−x)′=e−x(1+e−x)2=1+e−x−1(1+e−x)2=11+e−x⋅(1−11+e−x)=σ(x)(1−σ(x)) \begin{aligned} (\frac{1}{1+e^{-x}})'&=\frac{e^{-x}}{(1+e^{-x})^2} \\ &=\frac{1+e^{-x}-1}{(1+e^{-x})^2} \\ &=\frac{1}{1+e^{-x}}\cdot (1-\frac{1}{1+e^{-x}}) \\ &=\sigma(x) (1-\sigma(x)) \end{aligned} (1+e−x1)′=(1+e−x)2e−x=(1+e−x)21+e−x−1=1+e−x1⋅(1−1+e−x1)=σ(x)(1−σ(x))

因为y^=σ(θX)\hat{y}=\sigma(\theta X)y^=σ(θX)，我们将它带入损失函数，可以得到，其中σ(θ)=σ(θX)\sigma(\theta)=\sigma(\theta X)σ(θ)=σ(θX)：

J(θ)=−1mYlog⁡σ(θ)+(1−Y)log⁡(1−σ(θ))J(\theta)=-\frac{1}{m}Y\log \sigma(\theta) + (1 - Y)\log( 1- \sigma(\theta))J(θ)=−m1Ylogσ(θ)+(1−Y)log(1−σ(θ))

接着我们求J(θ)J(\theta)J(θ)对θ\thetaθ的偏导，这里要代入上面对σ(x)\sigma(x)σ(x)求导的结论：

∂∂θJ(θ)=−1m(Y⋅1σ(θ)⋅σ′(θ)+(1−Y)⋅11−σ(θ)⋅σ′(θ)⋅(−1))=−1m(Y⋅1σ(θ)⋅σ(θ)(1−σ(θ))⋅X−(1−Y)⋅11−σ(θ)⋅σ(θ)(1−σ(θ))⋅X)=−1m(Y(1−σ(θ))−σ(θ)+Y⋅σ(θ))⋅X=−1m(σ(θ)−Y)⋅X=−1m(Y^−Y)⋅X \begin{aligned} \frac{\partial}{\partial \theta}J(\theta)&=-\frac{1}{m}(Y\cdot \frac{1}{\sigma(\theta)}\cdot \sigma'(\theta)+(1-Y)\cdot \frac{1}{1-\sigma(\theta)}\cdot \sigma'(\theta)\cdot(-1)) \\ &=-\frac{1}{m}(Y\cdot \frac{1}{\sigma(\theta)}\cdot \sigma(\theta)(1-\sigma(\theta))\cdot X-(1-Y)\cdot \frac{1}{1-\sigma(\theta)}\cdot \sigma(\theta)(1-\sigma(\theta))\cdot X) \\ &=-\frac{1}{m}(Y(1-\sigma(\theta)) - \sigma(\theta)+Y\cdot \sigma(\theta))\cdot X\\ &=-\frac{1}{m}(\sigma(\theta) - Y)\cdot X\\ &=-\frac{1}{m}(\hat{Y} - Y)\cdot X \end{aligned} ∂θ∂J(θ)=−m1(Y⋅σ(θ)1⋅σ′(θ)+(1−Y)⋅1−σ(θ)1⋅σ′(θ)⋅(−1))=−m1(Y⋅σ(θ)1⋅σ(θ)(1−σ(θ))⋅X−(1−Y)⋅1−σ(θ)1⋅σ(θ)(1−σ(θ))⋅X)=−m1(Y(1−σ(θ))−σ(θ)+Y⋅σ(θ))⋅X=−m1(σ(θ)−Y)⋅X=−m1(Y^−Y)⋅X

代码实战

梯度的公式都推出来了，离写代码实现还远吗？

不过巧妇难为无米之炊，在我们撸模型之前，我们先试着造一批数据。

我们选择生活中一个很简单的场景——考试。假设每个学生需要参加两门考试，两门考试的成绩相加得到最终成绩，我们有一批学生是否合格的数据。希望设计一个逻辑回归模型，帮助我们直接计算学生是否合格。

为了防止sigmoid函数产生偏差，我们把每门课的成绩缩放到(0, 1)的区间内。两门课成绩相加超过140分就认为总体及格。

import numpy as np
def load_data():
    X1 = np.random.rand(50, 1)/2 + 0.5
    X2 = np.random.rand(50, 1)/2 + 0.5
    y = X1 + X2
    Y = y > 1.4
    Y = Y + 0
    x = np.c_[np.ones(len(Y)), X1, X2]
    return x, Y

这样得到的训练数据有两个特征，分别是学生两门课的成绩，还有一个偏移量1，用来记录常数的偏移量。

接着，根据上文当中的公式，我们不难（真的不难）实现sigmoid以及梯度下降的函数。

def sigmoid(x):
    return 1.0/(1+np.exp(-x))
def gradAscent(data, classLabels):
    X = np.mat(data)
    Y = np.mat(classLabels)
    m, n = np.shape(dataMat)
    # 学习率
    alpha = 0.01
    iterations = 10000
    wei = np.ones((n, 1))
    for i in range(iterations):
        y_hat = sigmoid(X * wei)
        error = Y - y_hat
        wei = wei + alpha * X.transpose()*error
    return wei

这段函数实现的是批量梯度下降，对Numpy熟悉的同学可以看得出来，这就是在直接套公式。

最后，我们把数据集以及逻辑回归的分割线绘制出来。

import matplotlib.pyplot as plt
def plotPic():
    dataMat, labelMat = load_data()
    #获取梯度
    weis = gradAscent(dataMat, labelMat).getA()
    n = np.shape(dataMat)[0]
    xc1 = []
    yc1 = []
    xc2 = []
    yc2 = []
    #数据按照正负类别划分
    for i in range(n):
        if int(labelMat[i]) == 1:
            xc1.append(dataMat[i][1])
            yc1.append(dataMat[i][2])
        else:
            xc2.append(dataMat[i][1])
            yc2.append(dataMat[i][2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xc1, yc1, s=30, c='red', marker='s')
    ax.scatter(xc2, yc2, s=30, c='green')
    #绘制分割线
    x = np.arange(0.5, 1, 0.1)
    y = (-weis[0]- weis[1]*x)/weis[2]
    ax.plot(x, y)
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.show()

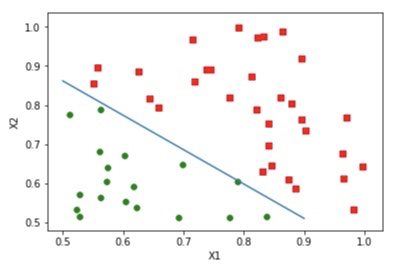
最后得到的结果如下：

随机梯度下降版本

可以发现，经过了1万次的迭代，我们得到的模型已经可以正确识别所有的样本了。

我们刚刚实现的是全量梯度下降算法，我们还可以利用随机梯度下降来进行优化。优化也非常简单，我们计算梯度的时候不再是针对全量的数据，而是从数据集中选择一条进行梯度计算。

基本上可以复用梯度下降的代码，只需要对样本选取的部分加入优化。

def stocGradAscent(data, classLab, iter_cnt):
    X = np.mat(data)
    Y = np.mat(classLab)
    m, n = np.shape(dataMat)
    weis = np.ones((n, 1))
    for j in range(iter_cnt):
        for i in range(m):
            # 使用反比例函数优化学习率
            alpha = 4 / (1.0 + j + i) + 0.01
            randIdx = int(np.random.uniform(0, m))
            y_hat = sigmoid(np.sum(X[randIdx] * weis))
            error = Y[randIdx] - y_hat
            weis = weis + alpha * X[randIdx].transpose()*error
    return weis

我们设置迭代次数为2000，最后得到的分隔图像结果如下：

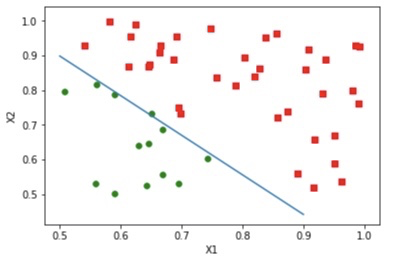
当然上面的代码并不完美，只是一个简单的demo，还有很多改进和优化的空间。只是作为一个例子，让大家直观感受一下：其实自己亲手写模型并不难，公式的推导也很有意思。这也是为什么我会设置高数专题的原因。CS的很多知识也是想通的，在学习的过程当中灵感迸发旁征博引真的是非常有乐趣的事情，希望大家也都能找到自己的乐趣。

今天的文章就是这些，如果觉得有所收获，请顺手扫码点个关注吧，你们的举手之劳对我来说很重要。