线性代数求行列式的值(用C++程序轻松解决)
C++代码实现行列式求值行列式求值的基本思路思路一——行列式展开不利用辅助函数的递归:辅助函数递归奉上一个完整代码,可以直接根据提示计算思路二——逆序数全排列思路三——初等变换调试分析
线性代数行列式求值算的可真是让人CPU疼,但计算机是不累的,所以用一个c++程序帮助你验证求解行列式的值吧。 行列式求值的基本思路
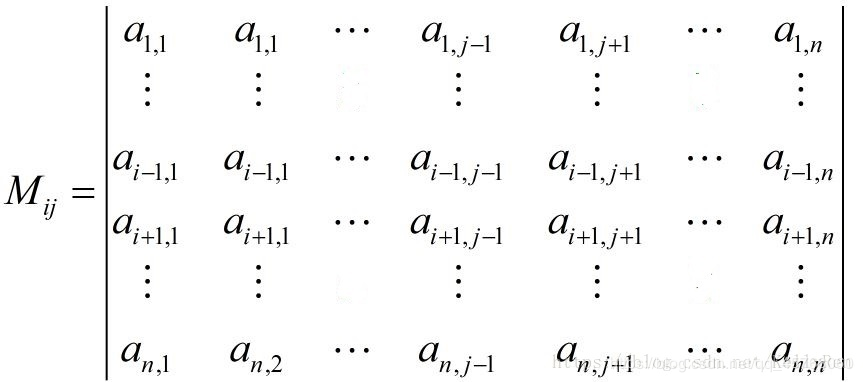 代数余子式:
代数余子式:
余子式再乘以-1的i+j次方(ij为行列式的行和列)

**我们可以看到行列式展开得到的代数余子式又是一个行列式,这是一个逐步求精的过程。显然可以用递归的方法。
基本算法: 行列式按第一行展开: 循环求各个元素与其对应代数余子式乘积的和。 其中余子式求值递归为行列式求值 递归终止条件:
行列式阶数为1,返回该数
作者:缄xp
线性代数行列式求值算的可真是让人CPU疼,但计算机是不累的,所以用一个c++程序帮助你验证求解行列式的值吧。 行列式求值的基本思路
行列式求值主要有以下这几种思路:
行列式等于它的任意列(或行)各个元素与其对应代数余子式乘积的和。 直接利用行列式的定义(逆序数)求解 利用行列式的性质做初等变换在求解: 性质1:互换行列式的两列(或两行),行列式仅改变符号。 性质2:行列式某行(或某列)的 k 倍加到另一行(或列)上,行列式不变。 思路一——行列式展开首先再次介绍下余子式和代数余子式:
余子式:在 n 阶行列式中,把某个元素所在的行列都去掉之后,剩下的 n-1 阶行列式就叫做该元素的余子式: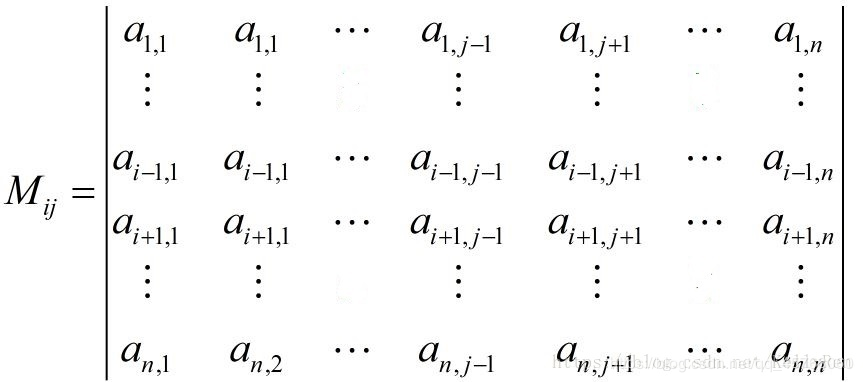 代数余子式:
代数余子式:余子式再乘以-1的i+j次方(ij为行列式的行和列)

**我们可以看到行列式展开得到的代数余子式又是一个行列式,这是一个逐步求精的过程。显然可以用递归的方法。
基本算法: 行列式按第一行展开: 循环求各个元素与其对应代数余子式乘积的和。 其中余子式求值递归为行列式求值 递归终止条件:
行列式阶数为1,返回该数
下面给出两种递归的方法:**
不利用辅助函数的递归:代码如下:
double cal(double **det,int n)//det-行列式,n:行列式的阶数
{
double detVal = 0;//行列式的值
if(n == 1)//递归终止条件
return det[0][0];
double **tempdet = new double *[n-1];//用来存储余相应的余子式
for(int i=0;i<n-1;i++)
tempdet[i] = new double[n-1];
for(int i=0;i<n;i++)//第一重循环,行列式按第一行展开
{
for(int j=0;j<n-1;j++)
for(int k=0;k<n-1;k++)
{
if(k <i)
tempdet[j][k]=det[j+1][k] ;
else
tempdet[j][k]=det[j+1][k+1];
}
detVal += det[0][i] * pow(-1.0,i) * cal(tempdet,n-1);
}
return detVal;
}
辅助函数递归
这一种构建了一个辅助函数,可以更加直观的理解此递归算法
//获得det[i][j]余子式行列式
vector<vector > getComplementMinor(vector<vector > det,int i,int j) ;
//获得行列式det的值
double getDetVal(vector<vector > det);
//获得det[i][j]余子式行列式
vector<vector > getComplementMinor(vector<vector > det,int i,int j)
{
int n=det.size(),m=det[0].size();//n为det的行,m为det的列;
vector<vector > ans(n-1);//保存获得的结果
for(int k=0;k<n-1;k++)
for(int l=0;l<n-1;l++)
{
ans[k].push_back(det[k<i?k:k+1][l<j?l:l+1]);
}
return ans;
}
double getDetVal(vector<vector > det)
{
double ans=0;
int n=det.size(),m=det[0].size();//n为det的行,m为det的列;
if(n != m)
{
cout<<" 您输入的矩阵不是方阵!求么子行列式!";
exit(1);
}
if(det.size() == 1)
return det[0][0];
for(int i=0;i<m;i++)
{
ans+=det[0][i] * pow(-1,i)*getDetVal(getComplementMinor(det,0,i));
}
return ans;
}
奉上一个完整代码,可以直接根据提示计算
#include
using namespace std;
double cal(double **det,int n)//det-行列式,n:行列式的阶数
{
double detVal = 0;//行列式的值
if(n == 1)//递归终止条件
return det[0][0];
double **tempdet = new double *[n-1];//用来存储余相应的余子式
for(int i=0;i<n-1;i++)
tempdet[i] = new double[n-1];
for(int i=0;i<n;i++)//第一重循环,行列式按第一行展开
{
for(int j=0;j<n-1;j++)
for(int k=0;k<n-1;k++)
{
if(k <i)
tempdet[j][k]=det[j+1][k] ;
else
tempdet[j][k]=det[j+1][k+1];
}
detVal += det[0][i] * pow(-1.0,i) * cal(tempdet,n-1);
}
return detVal;
}
int main()
{
int n;
cout<> n;//输入行列式的阶数
double **det = new double *[n];//需要动态内存
for(int i=0;i<n;i++)
det[i] = new double[n];
cout<<" 输入行列式:"<<endl;
for(int i=0;i<n;i++)
for(int j=0;j> det[i][j];
cout<<" 该行列式的值为:"<<cal(det,n);
}
思路二——逆序数全排列
思路三——初等变换
调试分析
第一种方法在精度上较好,但计算的阶数有限;后两者运算速度会比较好。但是本人最近较忙,后两者暂未给出(不要打我)- . -。
做题时用第一种方法完全可以帮你解决线性代数的问题。
作者:缄xp