张正友相机标定法与3D坐标系构建(附Python代码)
在计算机视觉的学习中,我们经常需要使用到相机的参数。但是,相机的参数往往是不容易得到的。比如我们使用相机去拍照时,这时相机的参数需要自己通过实验得出。本文将简要介绍获取相机参数的标定方法——张正友标定法。
一、棋盘格的生成在张正友相机标定法中,用到的标定板是类似于国际象棋的棋盘格。
在这里,我使用OpenCV函数生成了一个9×16的棋盘格。(棋盘格的规格可以根据自己电脑的显示屏分辨率进行调整,我的显示屏分辨率是1920×1080,因此每一个格子像素大小是120×120)
下面是棋盘格生成的Python代码:
import cv2
import sys
import numpy as np
image = np.ones([1080, 1920, 3], np.uint8) * 255 # 棋盘格的规格
x_nums = 16
y_nums = 9
square_pixel = 120 # 每个格子的大小是120×120
x0 = square_pixel
y0 = square_pixel
# 棋盘格生成
def DrawSquare():
flag = -1
for i in range(y_nums):
flag = 0 - flag
for j in range(x_nums):
if flag > 0:
color = [0,0,0]
else:
color = [255,255,255]
cv2.rectangle(image,(x0 + j*square_pixel,y0 + i*square_pixel),
(x0 + j*square_pixel+square_pixel,y0 + i*square_pixel+square_pixel),color,-1)
flag = 0 - flag
cv2.imwrite('/chessboard.bmp',image)
if __name__ == '__main__':
DrawSquare()
棋盘格生成之后,你可以选择打印出来,也可以选择直接在电脑上显示。当然,个人推荐打印出来较为方便。
二、相机标定 1.什么是相机标定?相机标定就是通过某种方法,利用特定图像求出相机的内参数和畸变系数。在本文中,我使用的标定方法是张正友标定法,是指张正友教授于1998年提出的单平面棋盘格的摄像机标定方法。该方法可以不需要特殊的标定物,只需要一张打印出来的棋盘格。为相机标定提供了很大便利,并且具有很高的精度。
2.基本原理张正友标定法是一种常用的标定方法,通过求解棋盘面到棋盘面图像的单应变换,从而求出相机的内参数和畸变系数。该法有相关的论文,感兴趣的盆友可以去看原文。论文的标题是:
A Flexible New Techniquefor Camera Calibration
Zhengyou Zhang, Senior Member, IEEE
原理简要概括起来就是:
•标定物的世界坐标已知
•图像像素坐标可通过特征点检测算法得到
•构成多个世界坐标到图像像素坐标的对应点对
•从而可以解算参数
算法流程:
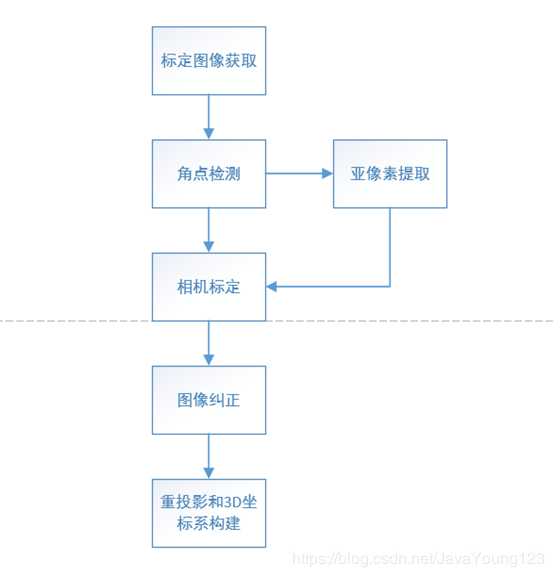
将标定板固定在一个平坦的平面上,使用相机去拍取10——20张图片作为准备要标定的图片。在拍照时,可以固定相机去移动标定板,也可以固定标定板去移动相机。这一步很重要,确保你拍的照片有很好的光照,并且图案是从不同的角度拍摄的,还要确保图案位于屏幕的不同部分。最好是整个棋盘格充满图像。
2.2 角点检测角点检测也称为特征点检测,是计算机视觉系统中获取图像特征的一种方法。内角点指的是标定板上不挨着边界的角点,我所用的标定板角点数是8×15。使用一个固定窗口在图像上进行任意方向上的滑动,比较滑动前与滑动后两种情况,窗口中的像素灰度变化程度,如果存在任意方向上的滑动,都有着较大灰度变化,那么我们可以认为该窗口中存在角点。
在程序中直接使用了OpenCV的findChessboardCorners()函数来检测角点。在这里,我设置了一个标志ret,如果ret为true,说明检测角点成功。ret为false的图像说明检测不成功,会影响程序的运行,所以需要人工去除检测角点失败的图像。
上述的角点检测可以得到一个大约的坐标,要精确确定它们的位置,可以使用cornerSubPix()函数,得到更加精确的亚像素级角点坐标。最后,使用drawChessboardCorners()函数绘制出被成功标定的角点。如图所示:

直接使用OpenCV中的calibrateCamera()函数来进行标定,求出了相机的内参数矩阵、畸变系数、旋转矩阵和平移向量。
代码如下:
import cv2
import numpy as np
import glob
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001) # 设置最佳迭代终止条件
world = np.zeros((8 * 15, 3), np.float32)
world[:, :2] = np.mgrid[0:15, 0:8].T.reshape(-1, 2)
world_points = []
image_points = []
images = glob.glob('/img*.jpg') # 输入图像路径
calibrated_images = []
for image in images:
img = cv2.imread(image)
gray_image = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 把BGR图像转化为灰度图像
size = gray_image.shape[::-1]
ret, corners = cv2.findChessboardCorners(gray_image, (15, 8), None) # 角点检测
print(ret)
if ret:
world_points.append(world)
corners_subpixel = cv2.cornerSubPix(gray_image, corners, (5, 5), (-1, -1), criteria)
# 寻找亚像素点
if [corners_subpixel]:
image_points.append(corners_subpixel)
else:
image_points.append(corners)
cv2.drawChessboardCorners(img, (15, 8), corners, ret) # 画出成功检测的角点
calibrated_images.append(img)
print(len(image_points)) # 图像的数量
# 相机标定
ret, camera_matrix, distortion_coefficient, r_vectors, t_vectors = cv2.calibrateCamera(world_points, image_points, size, None, None)
# 输出相机的内参数矩阵、畸变系数、旋转矩阵和平移向量
print("camera matrix:\n", camera_matrix)
print("distortion coefficient:\n", distortion_coefficient)
print("rotation vectors:\n", r_vectors)
print("translation vectors:\n", t_vectors)
三、3D坐标系构建
1.图像纠正
由于光线投射导致实际对象物体跟投影到2D平面的图像不一致,幸运的是这种不一致性是稳定的,我们可以通过对相机标定,计算出畸变参数来实现对后续图像的畸变校正。关于畸变类型,常见的图像畸变类型有径向与切向畸变。张正友标定法主要考虑的是径向畸变。
使用getOptimalNewCameraMatrix()函数求出优化的相机内参,然后再使用 undistort()函数进行图像径向畸变校正。
有了内部参数,畸变参数和旋转变换矩阵,我们就可以使用cv2.projectPoints()将对象点转换到图像点,进行反向投影。算反投影得到的点与图像上检测到的点的误差,最后计算一个对于所有标定图像的平均误差,这个值就是反投影误差。反投影误差可以评估结果的好坏。越接近0,说明结果越理想。
利用计算得到的相机内参数和畸变系数,就能进行3D Box的构建,即估计图像中图案的姿势。先设置好3D Box的8个三维顶点的坐标(根据实际棋盘格的物理尺寸来设计),然后利用K和R,t,投影到图像中得到8个顶点的二维投影坐标,然后基于二维投影坐标画二维直线即可。我创建了一个叫draw_3D_Box()的函数,绘制三维坐标轴,并连接检测成功的角点,构建3D Box。
代码续上:
# 获取优化后的相机内参
img2 = cv2.imread('/img.jpg')
h, w = img2.shape[:2]
new_camera_matrix, roi = cv2.getOptimalNewCameraMatrix(camera_matrix, distortion_coefficient, (w, h), 1,(w, h))
print("roi:"+str(roi))
dst = cv2.undistort(img2, camera_matrix, distortion_coefficient, None, new_camera_matrix) # 图像校正
cv2.imwrite('/undistort_img.jpg', dst)
# 重投影误差
total_error = 0
for i in range(len(world_points)):
image_points2, _ = cv2.projectPoints(world_points[i], r_vectors[i], t_vectors[i], camera_matrix,distortion_coefficient)
error = cv2.norm(image_points[i], image_points2, cv2.NORM_L2) / len(image_points2)
total_error += error
mean_error = total_error / len(world_points)
print("Reprojection error: " + str(mean_error))
# 3D点
axis2 = np.float32([[0, 0, 0], [0, 3, 0], [3, 3, 0], [3, 0, 0], [0, 0, -3], [0, 3, -3], [3, 3, -3], [3, 0, -3]])
# 3D坐标系构建函数
def draw_3D_Box(img, corners, imgpts):
imgpts = np.int32(imgpts).reshape(-1, 2)
# 绿色背景
img = cv2.drawContours(img, [imgpts[:4]], -1, (0, 255, 0), -3)
for i, j in zip(range(4), range(4, 8)):
img = cv2.line(img, tuple(imgpts[i]), tuple(imgpts[j]), (255, 0, 0), 3)
img = cv2.drawContours(img, [imgpts[4:]], -1, (0, 0, 255), 3)
return img
# 用PnP算法获取旋转矩阵和平移向量
_, r_vectors, t_vectors, inliers = cv2.solvePnPRansac(world, corners_subpixel, camera_matrix, distortion_coefficient)
# 重投影
imgpts, jac = cv2.projectPoints(axis2, r_vectors, t_vectors, camera_matrix, distortion_coefficient)
# 3D坐标系构建
outcome_image = draw_3D_Box(dst, corners_subpixel, imgpts)
cv2.imwrite('/outcome_img.jpg', outcome_image)
最后的效果如下:

大功告成!
作者:★海阔天空♂