Java数据结构之线段树中的懒操作详解
目录
一、问题提出
二、区间更新
三、区间查询
四、实战
1.问题描述
2.输入
3.代码
4.测试
一、问题提出对于线段树,若要求对区间中的所有点都进行更新,可以引入懒操作。
懒操作包括区间更新和区间查询操作。
二、区间更新对 [l,r] 区间进行更新,例如将 [l,r] 区间所有元素都更新为 v,步骤如下。
1.若当前节点区间被查询区间[l,r]覆盖,则仅对该节点进行更新并做懒标记,表示该节点已被更新,对该节点的子节点暂不更新。
2.判断是在左子树中查询还是在右子树中查询。在查询过程中,若当前节点带有懒标记,则将懒标记传给子节点(将当前节点的懒标记清除,将子节点更新并做懒标记),继续查找。
3.在返回时更新最值。
三、区间查询带有懒标记的区间查询和普通的区间查询有所不同,在查询过程中若遇到节点有懒标记,则下传懒标记,继续查询。
四、实战 1.问题描述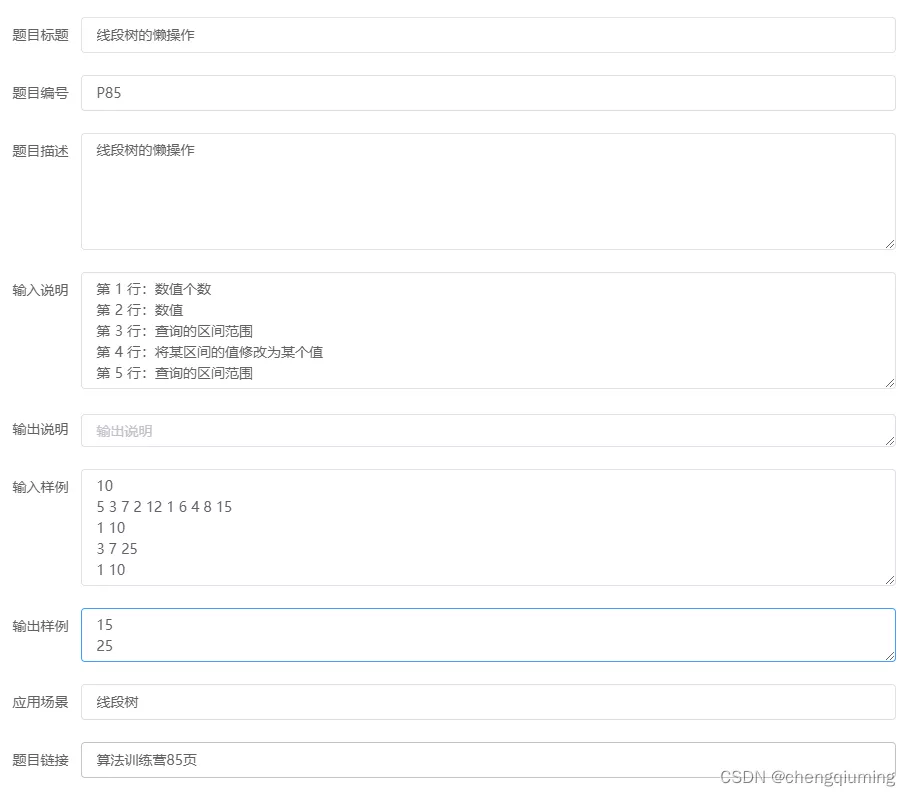
3.代码10
5 3 7 2 12 1 6 4 8 15
3 7 25
1 10
package com.platform.modules.alg.alglib.p85;
public class P85 {
public String output = "";
private final int maxn = 100005;
private final int inf = 0x3f3f3f3f;
private int n;
private int a[] = new int[maxn];
private node tree[] = new node[maxn * 4]; // 树结点存储数组
public P85() {
for (int i = 0; i < tree.length; i++) {
tree[i] = new node();
}
}
void lazy(int k, int v) {
tree[k].mx = v; // 更新最值
tree[k].lz = v; // 做懒标记
}
// 向下传递懒标记
void pushdown(int k) {
lazy(2 * k, tree[k].lz); // 传递给左孩子
lazy(2 * k + 1, tree[k].lz); // 传递给右孩子
tree[k].lz = -1; // 清除自己的懒标记
}
// 创建线段树,k表示存储下标,区间[l,r]
void build(int k, int l, int r) {
tree[k].l = l;
tree[k].r = r;
tree[k].lz = -1; // 初始化懒操作
if (l == r) {
tree[k].mx = a[l];
return;
}
int mid, lc, rc;
mid = (l + r) / 2; // 划分点
lc = k * 2; // 左孩子存储下标
rc = k * 2 + 1; // 右孩子存储下标
build(lc, l, mid);
build(rc, mid + 1, r);
tree[k].mx = Math.max(tree[lc].mx, tree[rc].mx); // 结点的最大值等于左右孩子最值的最大值
}
// 将区间 [l,r] 修改更新为 v
void update(int k, int l, int r, int v) {
// 找到该区间
if (tree[k].l >= l && tree[k].r <= r) {
lazy(k, v); // 更新并做懒标记
return;
}
if (tree[k].lz != -1)
pushdown(k); // 懒标记下移
int mid, lc, rc;
mid = (tree[k].l + tree[k].r) / 2; // 划分点
lc = k * 2; // 左孩子存储下标
rc = k * 2 + 1; // 右孩子存储下标
if (l <= mid)
update(lc, l, r, v); // 到左子树更新
if (r > mid)
update(rc, l, r, v);// 到右子树更新
tree[k].mx = Math.max(tree[lc].mx, tree[rc].mx); // 返回时修改更新最值
}
// 求区间 [l,r] 的最值
int query(int k, int l, int r) {
int Max = -inf;
if (tree[k].l >= l && tree[k].r <= r) // 找到该区间
return tree[k].mx;
if (tree[k].lz != -1)
pushdown(k); // 懒标记下移
int mid, lc, rc;
mid = (tree[k].l + tree[k].r) / 2; // 划分点
lc = k * 2; // 左孩子存储下标
rc = k * 2 + 1; // 右孩子存储下标
if (l <= mid)
Max = Math.max(Max, query(lc, l, r)); // 到左子树查询
if (r > mid)
Max = Math.max(Max, query(rc, l, r)); // 到右子树查询
return Max;
}
public String cal(String input) {
int l, r;
int i, v;
String[] line = input.split("\n");
n = Integer.parseInt(line[0]); // 第 1 行:10
String[] nums = line[1].split(" ");
// 第 2 行:5 3 7 2 12 1 6 4 8 15
for (i = 1; i <= n; i++)
a[i] = Integer.parseInt(nums[i - 1]);
build(1, 1, n); // 创建线段树
// 输入查询最值的区间 [l,r] 1 10
String[] range = line[2].split(" ");
l = Integer.parseInt(range[0]);
r = Integer.parseInt(range[1]);
// 求区间[l..r]的最值
output += query(1, l, r) + "\n";
// 输入更新的区间值 l r v 第 3 行: 3 7 25
String[] change = line[3].split(" ");
l = Integer.parseInt(change[0]);
r = Integer.parseInt(change[1]);
v = Integer.parseInt(change[2]);
// 将区间 [l,r] 修改更新为 v
update(1, l, r, v);
// 求区间[l..r]的最值 第 4 行:1 10
range = line[4].split(" ");
l = Integer.parseInt(range[0]);
r = Integer.parseInt(range[1]);
// 求区间 [l..r] 的最值
output += query(1, l, r) + "\n";
return output;
}
}
// 结点
class node {
int l; // l 表示区间左右端点
int r; // r 表示区间左右端点
int mx; // mx表示区间[l,r]的最值
int lz; // lz 懒标记
}
4.测试

以上就是Java数据结构之线段树中的懒操作详解的详细内容,更多关于Java线段树 懒操作的资料请关注软件开发网其它相关文章!