线段树（Segment Tree）

版权声明：本文为CSDN博主「Alex_McAvoy」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/u011815404/article/details/87277945

目录【概述】【基础操作实现】1.建树1）思路2）实现2.单点查询1）思路2）实现3.单点修改1）思路2）实现4.区间查询1）思路2）实现5.区间修改1）思路2）实现【模版】1.单点更新+区间查询2.区间更新+区间查询 【概述】

线段树是一种二叉搜索树，其存储的是一个区间的信息，每个结点以结构体的形式去存储，每个结构体包含三个元素：区间左端点、区间有端点、该区间要维护的信息（视实际情况而定），其基本思想是分治的思想。

线段树维护的信息，需要满足可加性，即能以可以接受的速度合并信息和修改信息，包括在使用懒惰标记时，标记也要满足可加性。（例如取模就不满足可加性，对 444 取模然后对 333 取模，两个操作就不能合并在一起做）

其特点是：

每个节点的左孩子区间范围为 [l，mid][l，mid][l，mid]，右孩子为 [mid+1,r][mid+1,r][mid+1,r] 对于结点 kkk，左孩子结点为 2∗k2*k2∗k，右孩子为 2∗k+12*k+12∗k+1，符合完全二叉树的性质

线段树一般结构如图：

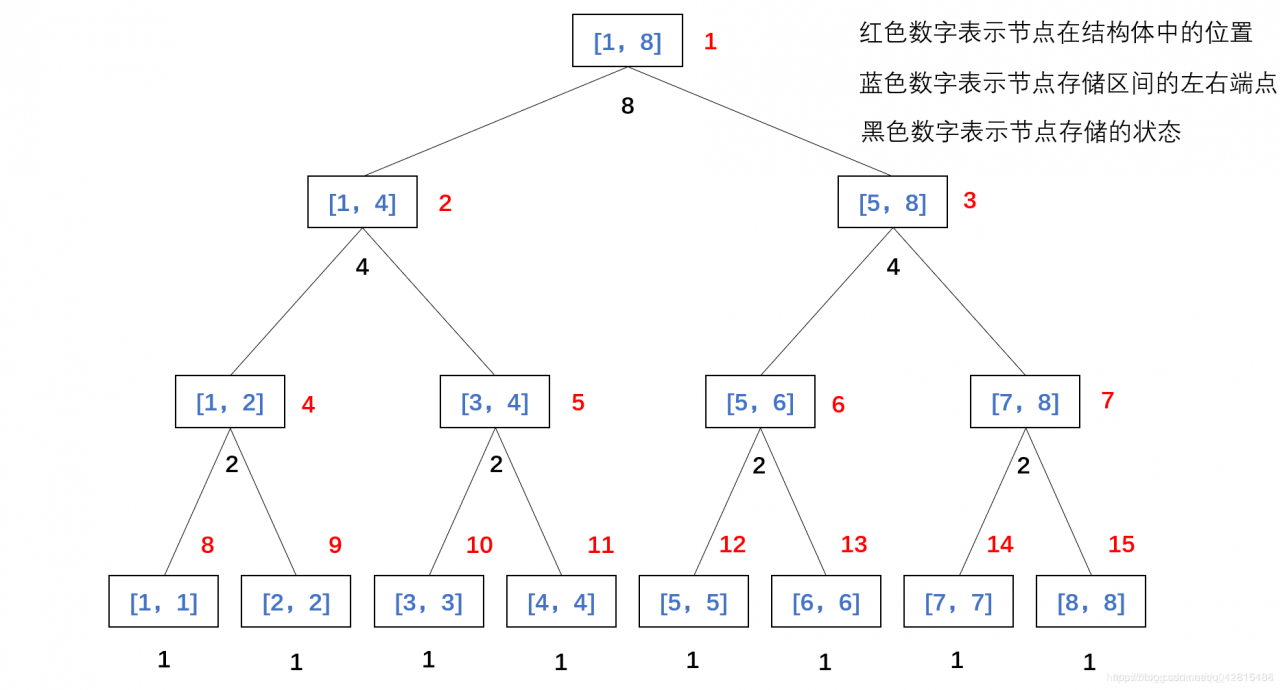【基础操作实现】

线段树的基础操作主要有 5 个：建树、单点查询、单点修改、区间查询、区间修改。

以下的实现均以求区间和为例。

结点：

struct node { int l, r; //区间左右端点 int w; //区间和 }tree[4*n+1]; //树开4倍空间。 1.建树 1）思路 对于二分到的每一个结点，给它的左右端点确定范围 如果是叶子节点，存储要维护的信息 状态合并 2）实现 void build(int l, int r, int k) { tree[k].l = l; tree[k].r = r; if(l==r) //叶子节点 { scanf("%d", &tree[k].w); return; } int mid = (l+r)/2; buildTree(l, mid, k*2); //左孩子 buildTree(mid+1, r, k*2+1); //右孩子 tree[k].w = tree[k*2].w + tree[k*2+1].w; //状态合并，此结点的w=两个孩子的w和 } 2.单点查询 1）思路

单点查询即查询一个点的状态，其查询方法与二分查询法基本一致。

若当前枚举的点左右端点相等，即为叶节点时，就是最终的目标节点。

若当前枚举的点左右端点不等，设查询位置为 xxx，当前结点区间范围为 l、rl、rl、r，中点为 midmidmid，则若 x<=midx<=midx<=mid，则递归它的左孩子，否则递归它的右孩子。

2）实现 void queryNode(int k) { if(tree[k].l==tree[k].r) //当前结点的左右端点相等，为叶子节点，是最终答案 { ans = tree[k].w; return; } int mid = (tree[k].l+tree[k].r)/2; if(x<=mid) //目标位置比中点靠左，就递归左孩子 queryNode(k*2); else //反之，递归右孩子 queryNode(k*2+1); } 3.单点修改 1）思路

单点修改即更改某一个点的状态，对第 xxx 个数加上 yyy，其基本思想是结合单点查询的原理，找到 xxx 的位置，然后根据建树状态合并的原理，修改每个结点的状态。

2）实现 void updateNode(int k) { if(tree[k].l==tree[k].r) //找到目标位置 { tree[k].w += y; return; } int mid = (tree[k].l+tree[k].r)/2; if(x<=mid) //目标位置比中点靠左，就递归左孩子 updateNode(k*2); else //反之，递归右孩子 updateNode(k*2+1); tree[k].w = tree[k*2].w+tree[k*2+1].w; //所有包含结点k的结点状态更新 } 4.区间查询 1）思路

区间查询，即查询一段区间的状态

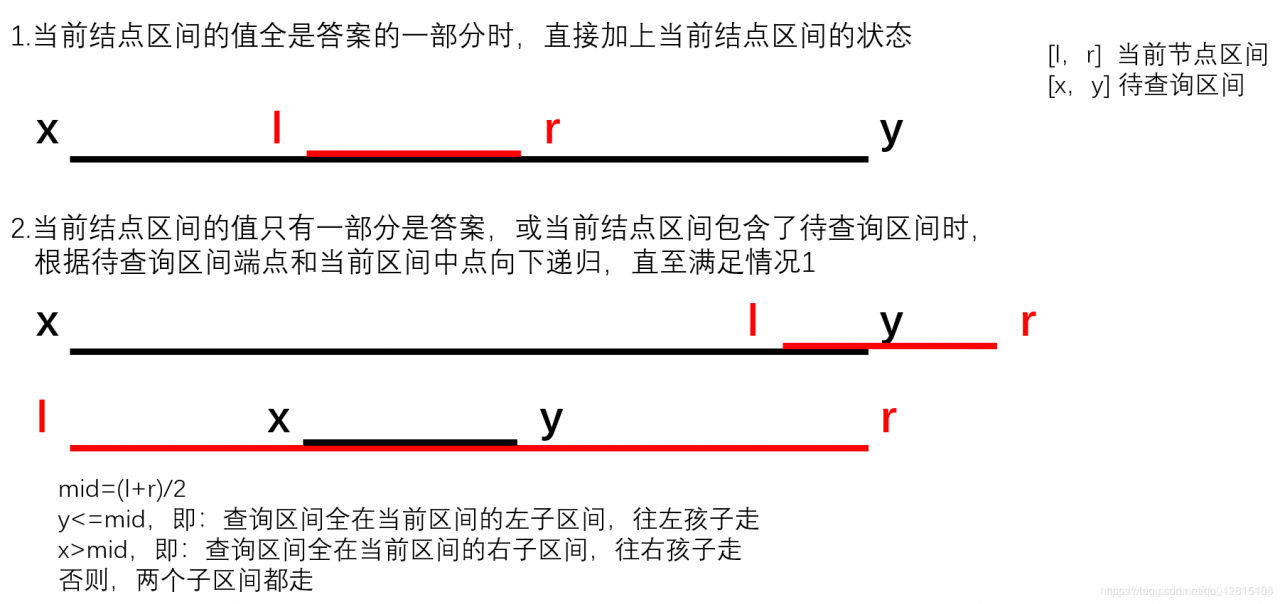2）实现 void queryInterval(int k,int x,int y) { if(tree[k].l>=x&&tree[k].r<=y) { ans += tree[k].w; return; } int mid = (tree[k].l+tree[k].r)/2; if(xmid) queryInterval(k*2+1, x, y); } 5.区间修改 1）思路

区间修改即修改一段连续区间的值，给区间 [a,b][a,b][a,b] 的每个数都加 xxx

线段树更新树时，为了避免更新而导致超时问题，因此每次修改只修改相对应的区间，然后记录一个延迟标记，其作用是：存储到这个节点的修改信息，暂时不把修改信息传到子节点。简单来说，每次更新的时候不要更新到底，用延迟标记使得更新延迟到下次需要更新 or 询问的时候。

下次更新或者查询的时候，如果查到该节点，就把延迟标记进行下传，将值加到他的子节点上去，同时将延迟标记变为 000，避免下次重复更新。这样只更新到查询的子区间，不需要再往下找了，极大的降低了时间复杂度。

以下图为例，一开始对区间 [1,4][1,4][1,4] 每个值都 +3+3+3，只有当需要对 [3,4][3,4][3,4] 区间查询时，才对下面的区间进行更新，其他区间无需更新。

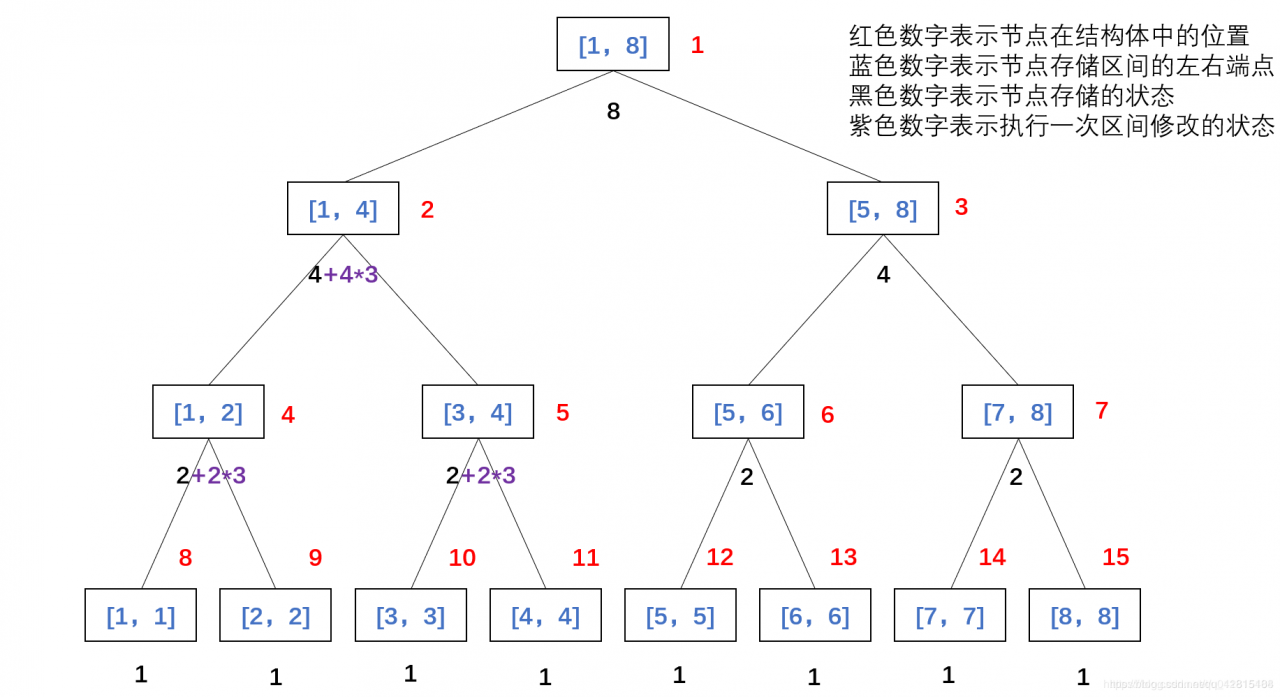
具体操作：

原结构体中增加新的变量，存储这个标记 递归到这个节点时，只更新这个节点的状态，并把当前的更改值累积到标记中 当需要递归这个节点的子节点时，标记下传给子节点，此时不必是哪个子节点，两个都传下去

下传操作的原理：

当前节点的标记累积到子节点的标记中 修改子节点状态，在当前的求和实例中，即原状态+子节点区间点的个数*父节点传下来的标记 父节点标记清 000 2）实现

标记下传：

void pushDown(int k) { tree[k*2].f += tree[k].f; //左孩子更新延迟标记 tree[k*2+1].f += tree[k].f; //右孩子更新延迟标记 tree[k*2].w += tree[k].f*(tree[k*2].r-tree[k*2].l+1); //左孩子状态更新 tree[k*2+1].w += tree[k].f*(tree[k*2+1].r-tree[k*2+1].l+1); //右孩子状态更新 tree[k].f = 0; //当前延迟标记清零 }

区间修改：

void updateInterval(int k,int x,int y) { if(tree[k].l>=x&&tree[k].r<=y) //当前区间全部对要修改的区间有用 { tree[k].w += (tree[k].r-tree[k].l+1)*x; //(r-1)+1区间点的总数 tree[k].f += x; return; } if(tree[k].f) //标记下传。只有不满足上面的if条件才执行，所以一定会用到当前节点的子节点 pushDown(k); int mid = (tree[k].l+tree[k].r)/2; if(xmid) updateInterval(k*2+1,x,y); tree[k].w = tree[k*2].w + tree[k*2+1].w; //更改区间状态 } 【模版】 1.单点更新+区间查询

以求和为例，具体情况根据题意

struct Node { int l, r; //左右区间 int sum; //区间和 }tree[N*4]; int a[N]; void pushUp(int i) //维护子结点 { tree[i].sum = tree[i*2].sum + tree[i*2+1].sum; } void build(int i, int l, int r) //建树 { tree[i].l = l; tree[i].r = r; if(l==r) //叶节点 { tree[i].sum = a[l]; //边输入边建树 //scanf("%d",&a[i]); return; } int mid = (l+r)>>1; build(i*2, l, mid); //结点的左儿子 build(i*2+1, mid+1, r); //结点的右儿子 pushUp(i); } //对id号点进行修改 void update(int i, int id, int val) //线段树单点修改 { if(tree[i].l==tree[i].r) { tree[i].sum += val; return; } int mid = (tree[i].l+tree[i].r)/2; if(idmid) update(i*2+1, id, val); pushUp(i); } int query(int i, int ql, int qr) //线段树区间查询 { if(ql=tree[i].r) //当前区间在目标区间内 return tree[i].sum; int mid = (tree[i].l+tree[i].r)/2; int res = 0; if(qlmid) res += query(i*2+1, ql, qr); return res; } int main() { int n, m; cin>>n; for(int i = 1; i >a[i]; build(1, 1, n); //先输入再建树 cin>>m; //m组询问 while(m--) { int p; cin>>p; if(p==1) //单点更新 { int id, val; cin>>id>>val; update(1, id, val); } else if(p==2) //区间查询 { int a, b; cin>>a>>b; cout<<query(1, a, b)<<endl; } } return 0; } 2.区间更新+区间查询 struct Node { int l, r; //左右区间 int sum; //区间和 int maxx, minn; //区间最值 int lazyAdd; //区间增值时的延迟标记 int lazySet; //区间赋值时的延迟标记 }tree[N*4]; int a[N]; int resSum, resMax, resMin; //存储结果 void pushDown(int i) //标记下传 { if(tree[i].lazySet!=-1) { tree[i*2].lazySet = tree[i*2+1].lazySet = tree[i].lazySet; tree[i*2].lazyAdd = tree[i*2+1].lazyAdd = 0; tree[i*2].minn = tree[i*2+1].minn = tree[i].lazySet; tree[i*2].maxx = tree[i*2+1].maxx = tree[i].lazySet; tree[i*2].sum = (tree[i*2].r-tree[i*2].l+1)*tree[i].lazySet; tree[i*2+1].sum = (tree[i*2+1].r-tree[i*2+1].l+1)*tree[i].lazySet; tree[i].lazySet = -1; } ///左子节点 tree[i*2].lazyAdd += tree[i].lazyAdd; //打上延迟标记 tree[i*2].minn += tree[i].lazyAdd; //更新 tree[i*2].maxx += tree[i].lazyAdd; //更新 tree[i*2].sum += tree[i].lazyAdd*(tree[i*2].r-tree[i*2].l+1); //更新 ///右子节点 tree[i*2+1].lazyAdd += tree[i].lazyAdd; //打上延迟标记 tree[i*2+1].minn += tree[i].lazyAdd; //更新 tree[i*2+1].maxx += tree[i].lazyAdd; //更新 tree[i*2+1].sum += tree[i].lazyAdd*(tree[i*2+1].r-tree[i*2+1].l+1); //更新 tree[i].lazyAdd=0;//清除标记 } void pushUp(int i) //维护子节点 { tree[i].sum = tree[i*2].sum + tree[i*2+1].sum; tree[i].maxx = max(tree[i*2].maxx, tree[i*2+1].maxx); tree[i].minn = min(tree[i*2].minn, tree[i*2+1].minn); } void build(int i, int l, int r) //建树 { tree[i].l = l; tree[i].r = r; tree[i].lazyAdd = 0; tree[i].lazySet = -1; if(l==r) //叶结点 { tree[i].sum = a[l]; tree[i].maxx = a[l]; tree[i].minn = a[l]; return; } int mid = (l+r)>>1; build(i*2, l, mid); //结点左儿子 build(i*2+1, mid+1, r);//结点右儿子 pushUp(i); } void updateSet(int i, int ql, int qr, int val) //区间修改，整体赋值为val { if(tree[i].l>=ql && tree[i].r<=qr) { tree[i].sum = val*(tree[i].r-tree[i].l+1); tree[i].minn = val; tree[i].maxx = val; tree[i].lazySet = val; tree[i].lazyAdd = 0; return; } pushDown(i);//标记下传 int mid = (tree[i].l+tree[i].r)/2; if(qlmid) updateSet(i*2+1, ql, qr, val); pushUp(i); } void updateAdd(int i, int ql, int qr, int val) //区间修改，整体+val { if(tree[i].l>=ql&&tree[i].r<=qr) { tree[i].sum += val*(tree[i].r-tree[i].l+1); tree[i].minn += val; tree[i].maxx += val; tree[i].lazyAdd += val; return; } pushDown(i); //标记下传 int mid = (tree[i].l+tree[i].r)/2; if(qlmid) updateAdd(i*2+1, ql, qr, val); pushUp(i); } void query(int i,int ql,int qr) //区间查询 { if(ql<=tree[i].l && tree[i].r<=qr) { resSum += tree[i].sum; resMax = max(resMax,tree[i].maxx); resMin = min(resMin,tree[i].minn); return ; } pushDown(i); int mid = (tree[i].l+tree[i].r)/2; if(qlmid) query(i*2+1, ql, qr); pushUp(i); } int main() { int n; cin>>n; for(int i = 1; i >a[i]; build(1, 1, n); int m; cin>>m; while(m--) { int p; cin>>p; if(p==1) //区间整体赋值 { int a, b; //区间 int val; //值 scanf("%d%d%d", &a, &b, &val); updateSet(1, a, b, val); } else if(p==2) //区间整体加值 { int a, b; //区间 int val; //值 scanf("%d%d%d", &a, &b, &val); updateAdd(1, a, b, val); } else if(p==3) //区间查询 { int a, b; cin>>a>>b; resSum = 0, resMax = -INF, resMin = INF; query(1, a, b); cout<<"Sum="<<resSum<<endl; cout<<"Max="<<resMax<<endl; cout<<"Min="<<resMin<<endl; } } return 0; }
作者：菜是原罪QAQ

segment tree 线段树