从GB到GBDT到XGBoost

boosting一句话理解：三个臭皮匠，顶个诸葛亮。
在计算机学习理论里，强可学习和弱可学习是等价的。
弱可学习模型转化为强可学习模型方法：前向分布加法模型。

yk+1 = yk + ( y-yk )
( y-yk )即为残差，每一个新的弱分类器学习的目标都是残差
这么一个简单的模型，能否得到我们想要的结果？
理论上( y-yk )只有方向是准确的，具体是多少是模糊的。

理论上( y-yk )只有方向是准确的，具体是多少是模糊的。
用梯度代替( y-yk )：
yk+1 = yk + ( ak *梯度)， ak为步长
这里的梯度就是我们常听说的伪残差，拟合伪残差得到方向，扫描搜索得到最好的步长。

使用指数函数为损失函数，即为Adaboost
使用决策树为分类器，即为GBDT
通过上述算法，我们(x,伪残差)得到方向g，（x,g）得到步长（单变量一元回归）

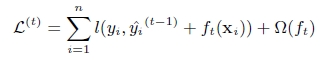
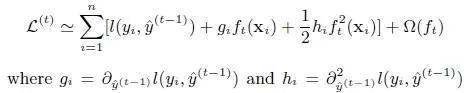
GBDT使用上述公式一阶泰勒展开
XGBoosting上述公式二阶泰勒展开
我们知道泰勒二阶展开就是牛顿法，直接求出了方向和步长，不需要线性搜索合适的步长。

XGBoosting上述公式二阶泰勒展开
我们知道泰勒二阶展开就是牛顿法，直接求出了方向和步长，不需要线性搜索合适的步长。
实际上处理不会一步到位，避免过拟合
详细推导见：https://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf link.
从这里可以看出XGBoost基本还是集成前人的东西，考虑大数据处理，优化并行计算，形成工业级应用才是XGBoost最大作用。

https://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf link.
https://arxiv.org/abs/1603.02754

xgboost gb gbdt