图像处理Task05图像分割/二值化

Tulla ·

更新时间:2024-11-14

· 909 次阅读

5.1简介

该部分的学习内容是对经典的阈值分割算法进行回顾，图像阈值化分割是一种传统的最常用的图像分割方法，因其实现简单、计算量小、性能较稳定而成为图像分割中最基本和应用最广泛的分割技术。它特别适用于目标和背景占据不同灰度级范围的图像。它不仅可以极大的压缩数据量，而且也大大简化了分析和处理步骤，因此在很多情况下，是进行图像分析、特征提取与模式识别之前的必要的图像预处理过程。图像阈值化的目的是要按照灰度级，对像素集合进行一个划分，得到的每个子集形成一个与现实景物相对应的区域，各个区域内部具有一致的属性，而相邻区域不具有这种一致属性。这样的划分可以通过从灰度级出发选取一个或多个阈值来实现。

5.2学习目标

1.了解阈值分割基本概念
2.理解最大类间方差法（大津法）、自适应阈值分割的原理
3.掌握OpenCV框架下上述阈值分割算法API的使用

5.3内容介绍

1、最大类间方差法、自适应阈值分割的原理
2、OpenCV代码实践

5.4算法理论介绍 5.4.1最大类间方差法（大津阈值法）

大津法（OTSU）是一种确定图像二值化分割阈值的算法，由日本学者大津于1979年提出。从大津法的原理上来讲，该方法又称作最大类间方差法，因为按照大津法求得的阈值进行图像二值化分割后，前景与背景图像的类间方差最大。

它被认为是图像分割中阈值选取的最佳算法，计算简单，不受图像亮度和对比度的影响，因此在数字图像处理上得到了广泛的应用。它是按图像的灰度特性，将图像分成背景和前景两部分。因方差是灰度分布均匀性的一种度量,背景和前景之间的类间方差越大,说明构成图像的两部分的差别越大,当部分前景错分为背景或部分背景错分为前景都会导致两部分差别变小。因此,使类间方差最大的分割意味着错分概率最小。

应用： 是求解图像全阈值的最佳方法，适用于大部分需要求图像全局阈值的场合。

优点： 计算简单快速，不受图像亮度和对比度的影响。

缺点： 对图像噪声敏感；只能针对单一目标分割；当目标和背景大小比例悬殊、类间方差函数可能呈现双峰或者多峰，这个时候效果不好。

算法原理介绍：

求类间方差：

OTSU算法的假设是存在阈值ThT_hTh将图像所有像素分为两类C1C_1C1(小于ThT_hTh)和C2C_2C2(大于ThT_hTh)，则这两类像素各自的均值就为m1m_1m1、m2m_2m2，图像全局均值为mgm_gmg。同时像素被分为C1C_1C1和C2C_2C2类的概率分别为p1p_1p1、p2p_2p2。因此就有：
p1∗m1+p2∗m2=mg(1) \begin{array}{c} p_1*m_1+p_2*m_2=m_g \end{array}(1) p1∗m1+p2∗m2=mg(1)

p1+p2=1(2) \begin{array}{c}p_1+p_2=1 \end{array} (2)p1+p2=1(2)

根据方差的概念，类间方差表达式为：

σ2=p1(m1−mg)2+p2(m2−mg)2(3) \begin{array}{c}\sigma ^2=p_1(m_1-m_g)^2+p_2(m_2-m_g)^2 \end{array} (3)σ2=p1(m1−mg)2+p2(m2−mg)2(3)

我们把上式化简，将(1)(1)(1)代入(3)(3)(3)，可得：

σ2=p1p2(m1−mg)2(4) \begin{array}{c}\sigma ^2=p_1p_2(m_1-m_g)^2 \end{array} (4)σ2=p1p2(m1−mg)2(4)

其中：

p1=∑i=0kpi(5) \begin{array}{c} p_1=\sum\limits_{i=0}^{k}p_i\end{array} (5)p1=i=0∑kpi(5)

pip_ipi是灰度像素为iii的像素点在一幅图像中出现的频率
m1=1p1∑i=0kipi(6) \begin{array}{c} m_1=\frac{1}{p_1}\sum\limits_{i=0}^{k}ip_i\end{array} (6)m1=p11i=0∑kipi(6)

m1=1p2∑i=k+1L−1ipi(7) \begin{array}{c} m_1=\frac{1}{p_2}\sum\limits_{i=k+1}^{L-1}ip_i\end{array} (7)m1=p21i=k+1∑L−1ipi(7)

其中，L=256L=256L=256，按公式遍历0~255个灰度级，求得能使上式最大化的灰度级KKK就是OTSU阈值了；
首先灰度级KKK的累加均值mmm和图像全局均值mgm_gmg分别为：
m=∑i=0kipi(8) \begin{array}{c} m=\sum\limits_{i=0}^{k}ip_i\end{array} (8)m=i=0∑kipi(8)

mg=∑i=0L−1ipi(9) \begin{array}{c} m_g=\sum\limits_{i=0}^{L-1}ip_i\end{array} (9)mg=i=0∑L−1ipi(9)

由式(6)(6)(6)得：

m1=1p1m(10) \begin{array}{c}m_1=\frac{1}{p_1}m \end{array} (10)m1=p11m(10)

m1=1p2(mg−m)(11) \begin{array}{c}m_1=\frac{1}{p_2}(m_g-m) \end{array} (11)m1=p21(mg−m)(11)
式(10),(11)(10),(11)(10),(11)代入式(4)(4)(4),我们可以得到最终的类间方差公式：

σ2=(mg∗p1−m)2p1(1−p1)(4) \begin{array}{c}\sigma ^2=\frac{(m_g*p_1-m)^2}{p_1(1-p_1)} \end{array} (4)σ2=p1(1−p1)(mg∗p1−m)2(4)
根据公式(5),(8),(9)(5),(8),(9)(5),(8),(9)求得能使式(12)(12)(12)最大化的灰度级KKK就是OTSU的阈值

分割：

这个分割就是二值化，OpenCV给了以下几种方式，很简单，可以参考：
在这里插入图片描述

5.4.2自适应阈值

前面介绍了OTSU算法，但这算法属于全局阈值法，所以对于某些光照不均的图像，这种全局阈值分割的方法会显得苍白无力，如下图：
在这里插入图片描述显然，这样的阈值处理结果不是我们想要的，那么就需要一种方法来应对这样的情况。

这种办法就是自适应阈值法(adaptiveThreshold)，它的思想不是计算全局图像的阈值，而是根据图像不同区域亮度分布，计算其局部阈值，所以对于图像不同区域，能够自适应计算不同的阈值，因此被称为自适应阈值法。(其实就是局部阈值法)

如何确定局部阈值呢？可以计算某个邻域(局部)的均值、中值、高斯加权平均(高斯滤波)来确定阈值。值得说明的是：如果用局部的均值作为局部的阈值，就是常说的移动平均法。通过均值平滑图像实现自适应阈值的原理及方法在这里。

5.5基于OpenCV的实现

关于C++的实现
OTSU算法
自适应阈值算法
下面给出Python-OpenCV的实现：

a.简单阈值

在这里，问题直截了当。对于每个像素，应用相同的阈值。如果像素值小于阈值，则将其设置为0，否则将其设置为最大值。函数cv.threshold用于应用阈值。第一个参数是源图像，它应该是灰度图像。第二个参数是阈值，用于对像素值进行分类。第三个参数是分配给超过阈值的像素值的最大值。OpenCV提供了不同类型的阈值，这由函数的第四个参数给出。通过使用cv.THRESH_BINARY类型。所有简单的阈值类型为：

cv.THRESH_BINARY
cv.THRESH_BINARY_INV
cv.THRESH_TRUNC
cv.THRESH_TOZERO
cv.THRESH_TOZERO_INV

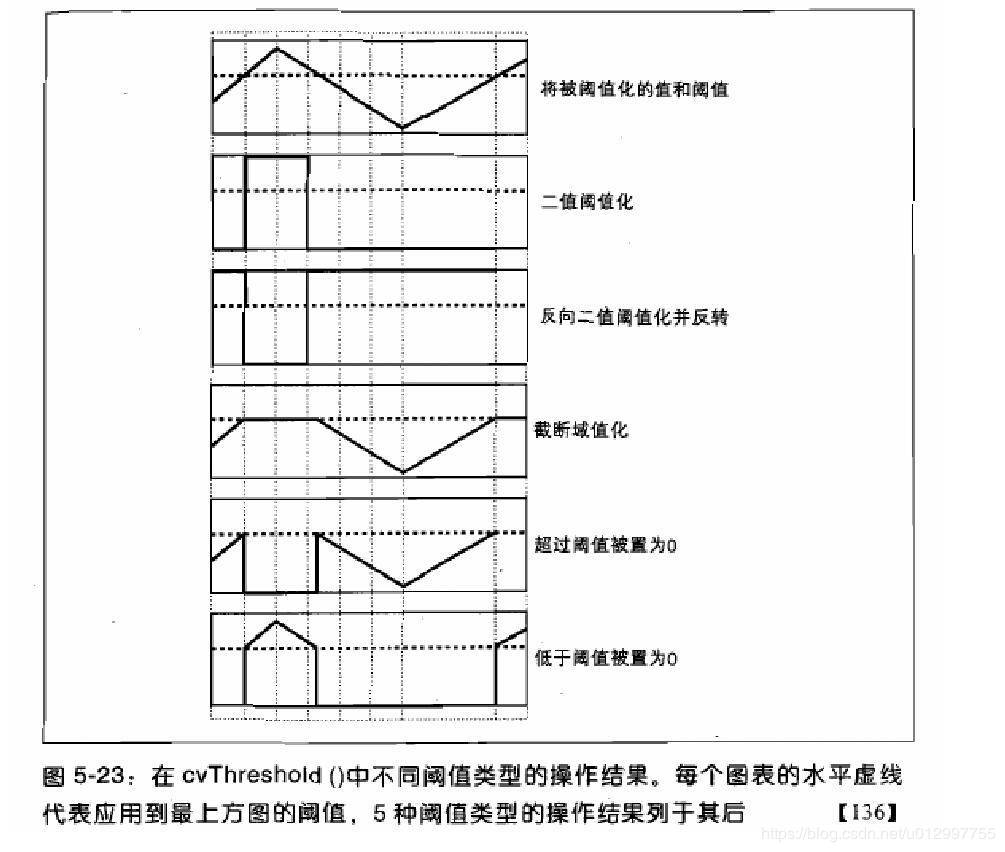在这里插入图片描述该方法返回两个输出。第一个是使用的阈值，第二个输出是阈值后的图像。

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
img = cv.imread('D:/Mechine_learning_data/lena512.bmp',0)
ret,thresh1 = cv.threshold(img,127,255,cv.THRESH_BINARY)
ret,thresh2 = cv.threshold(img,127,255,cv.THRESH_BINARY_INV)
ret,thresh3 = cv.threshold(img,127,255,cv.THRESH_TRUNC)
ret,thresh4 = cv.threshold(img,127,255,cv.THRESH_TOZERO)
ret,thresh5 = cv.threshold(img,127,255,cv.THRESH_TOZERO_INV)
titles = ['Original Image','BINARY','BINARY_INV','TRUNC','TOZERO','TOZERO_INV']
images = [img, thresh1, thresh2, thresh3, thresh4, thresh5]
print(ret)
for i in range(6):
    plt.subplot(2,3,i+1),plt.imshow(images[i],'gray')
    plt.title(titles[i])
    plt.xticks([]),plt.yticks([])
plt.show()

输出结果为：
在这里插入图片描述

b.自适应阈值

在上一节中，我们使用一个全局值作为阈值。但这可能并非在所有情况下都很好，例如，如果图像在不同区域具有不同的光照条件。在这种情况下，自适应阈值阈值化可以提供帮助。在此，算法基于像素周围的小区域确定像素的阈值。因此，对于同一图像的不同区域，我们获得了不同的阈值，这为光照度变化的图像提供了更好的结果。

这种方法需要我们指定三个参数，返回值只有一个。
Adaptive Method 指定计算阀值的方法
-cv2.ADAPTIVE_THRESH_MEAN_C:阀值取自相邻区域的平均值
-cv2.ADAPTIVE_THRESH_GAUSSIAN_C:阀值取自相邻区域的加权和，权重为一个高斯窗口
Block Size 邻域大小（用来计算阀值的区域大小）
C这就是一个常数，阀值就等于的平均值或者加权平均值减去这个常数

import cv2 
import numpy as np
from matplotlib import pyplot as plt
# 变成灰度图
img = cv2.imread('D:/Mechine_learning_data/55.jpg',cv2.IMREAD_GRAYSCALE)
#print(np.array(img).shape)
#中值滤波
img = cv2.medianBlur(img,5)
ret , th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
 # 11为block size，2为C值
th2 = cv2.adaptiveThreshold(img,255,cv2.ADAPTIVE_THRESH_MEAN_C , cv2.THRESH_BINARY,11,2 )
th3 = cv2.adaptiveThreshold(img,255,cv2.ADAPTIVE_THRESH_GAUSSIAN_C , cv2.THRESH_BINARY,11,2)
titles = ['original image' , 'global thresholding (v=127)','Adaptive mean thresholding',
          'adaptive gaussian thresholding']
images = [img,th1,th2,th3]
for i in range(4):
    plt.subplot(2,2,i+1),plt.imshow(images[i],'gray')
    plt.title(titles[i])
    plt.xticks([]),plt.yticks([])
plt.show()

输出结果为：
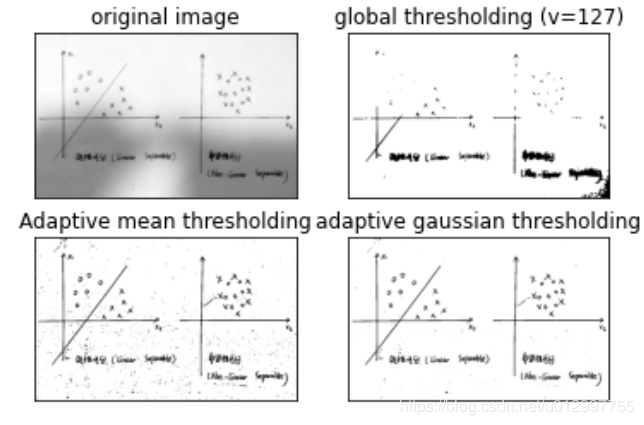在这里插入图片描述可以发现，用自适应阈值法将图像信息保留的更加完整。

c.OTSU的二值化

在全局阈值化中，我们使用任意选择的值作为阈值。相反，Otsu的方法避免了必须选择一个值并自动确定它的情况。

考虑仅具有两个不同图像值的图像（双峰图像），其中直方图将仅包含两个峰。一个好的阈值应该在这两个值的中间。类似地，Otsu的方法从图像直方图中确定最佳全局阈值。

为此，使用了cv.threshold作为附加标志传递。阈值可以任意选择。然后，算法找到最佳阈值，该阈值作为第一输出返回。

查看以下示例。输入图像为椒盐噪点图像。在第一种情况下，采用值为127的全局阈值。在第二种情况下，直接采用Otsu阈值法。在第三种情况下，首先使用中值滤波对图像进行滤波以去除噪声，然后应用Otsu阈值处理。了解噪声滤波如何改善结果。

import random
def sp_noise(image,prob):
    '''
    添加椒盐噪声
    prob:噪声比例 
    '''
    output = np.zeros(image.shape,np.uint8)
    thres = 1 - prob 
    for i in range(image.shape[0]):
        for j in range(image.shape[1]):
            rdn = random.random()
            if rdn  thres:
                output[i][j] = 255
            else:
                output[i][j] = image[i][j]
    return output
    img = cv2.imread('D:/Mechine_learning_data/lena512.bmp',cv2.IMREAD_GRAYSCALE)
src2 = sp_noise(img,0.05)
# 全局阈值
ret1,th1 = cv.threshold(src2,127,255,cv.THRESH_BINARY)
# Otsu阈值
ret2,th2 = cv.threshold(src2,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)
# 高斯滤波后再采用Otsu阈值
blur = cv.medianBlur(src2,5)
ret3,th3 = cv.threshold(blur,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)
print(ret2,ret3)
# 绘制所有图像及其直方图
images = [img, 0, th1,
          img, 0, th2,
          blur, 0, th3]
titles = ['Original Noisy Image','Histogram','Global Thresholding (v=127)',
          'Original Noisy Image','Histogram',"Otsu's Thresholding",
          'Gaussian filtered Image','Histogram',"Otsu's Thresholding"]
for i in range(3):
    plt.subplot(3,3,i*3+1),plt.imshow(images[i*3],'gray')
    plt.title(titles[i*3]), plt.xticks([]), plt.yticks([])
    plt.subplot(3,3,i*3+2),plt.hist(images[i*3].ravel(),256)
    plt.title(titles[i*3+1]), plt.xticks([]), plt.yticks([])
    plt.subplot(3,3,i*3+3),plt.imshow(images[i*3+2],'gray')
    plt.title(titles[i*3+2]), plt.xticks([]), plt.yticks([])
plt.show()

其中，用后两种方法得到的全局阈值分别为：116 117；
输出结果为：
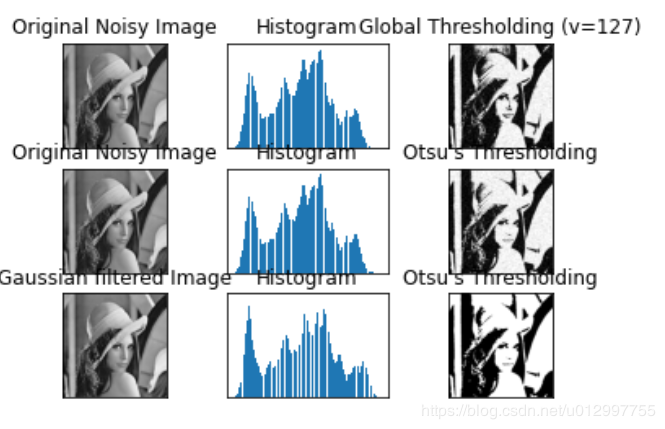在这里插入图片描述虽然不是双峰图像，但依然可以看出Otsu的作用

Otsu的二值化用Python代码的实现

σw2(t)=q1(t)σ12(t)+q2(t)σ22(t) \sigma_w^2(t) = q_1(t)\sigma_1^2(t)+q_2(t)\sigma_2^2(t) σw2(t)=q1(t)σ12(t)+q2(t)σ22(t)

q1(t)=∑i=1tP(i)&q2(t)=∑i=t+1IP(i) q_1(t) = \sum_{i=1}^{t} P(i) \quad \& \quad q_2(t) = \sum_{i=t+1}^{I} P(i) q1(t)=i=1∑tP(i)&q2(t)=i=t+1∑IP(i)

μ1(t)=∑i=1tiP(i)q1(t)&μ2(t)=∑i=t+1IiP(i)q2(t) \mu_1(t) = \sum_{i=1}^{t} \frac{iP(i)}{q_1(t)} \quad \& \quad \mu_2(t) = \sum_{i=t+1}^{I} \frac{iP(i)}{q_2(t)} μ1(t)=i=1∑tq1(t)iP(i)&μ2(t)=i=t+1∑Iq2(t)iP(i)

σ12(t)=∑i=1t[i−μ1(t)]2P(i)q1(t)&σ22(t)=∑i=t+1I[i−μ2(t)]2P(i)q2(t) \sigma_1^2(t) = \sum_{i=1}^{t} [i-\mu_1(t)]^2 \frac{P(i)}{q_1(t)} \quad \& \quad \sigma_2^2(t) = \sum_{i=t+1}^{I} [i-\mu_2(t)]^2 \frac{P(i)}{q_2(t)} σ12(t)=i=1∑t[i−μ1(t)]2q1(t)P(i)&σ22(t)=i=t+1∑I[i−μ2(t)]2q2(t)P(i)

实际上，它找到位于两个峰值之间的t值，以使两个类别的差异最小。它可以简单地在Python中实现，如下所示：

原理很简单，就是不断通过循环来迭代求出最合适的KKK值；

blur = cv.medianBlur(src2,5)
# 寻找归一化直方图和对应的累积分布函数
hist = cv.calcHist([blur],[0],None,[256],[0,256])
hist_norm = hist.ravel()/hist.max()
Q = hist_norm.cumsum()
bins = np.arange(256)
fn_min = np.inf
thresh = -1
for i in range(1,256):
    p1,p2 = np.hsplit(hist_norm,[i]) # 概率
    q1,q2 = Q[i],Q[255]-Q[i] # 对类求和
    b1,b2 = np.hsplit(bins,[i]) # 权重
    # 寻找均值和方差
    m1,m2 = np.sum(p1*b1)/q1, np.sum(p2*b2)/q2
    v1,v2 = np.sum(((b1-m1)**2)*p1)/q1,np.sum(((b2-m2)**2)*p2)/q2
    # 计算最小化函数
    fn = v1*q1 + v2*q2
    if fn < fn_min:
        fn_min = fn
        thresh = i
# 使用OpenCV函数找到otsu的阈值
ret, otsu = cv.threshold(blur,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)
print( "{} {}".format(thresh,ret) )

输出结果为：最优阈值为117，这与OpenCV自带的函数求解出来的结果一致；

The End

作者：习惯了看孤独的风景

图像分割二值化

1024 个赞