图像分割-阈值处理详解(未完成)
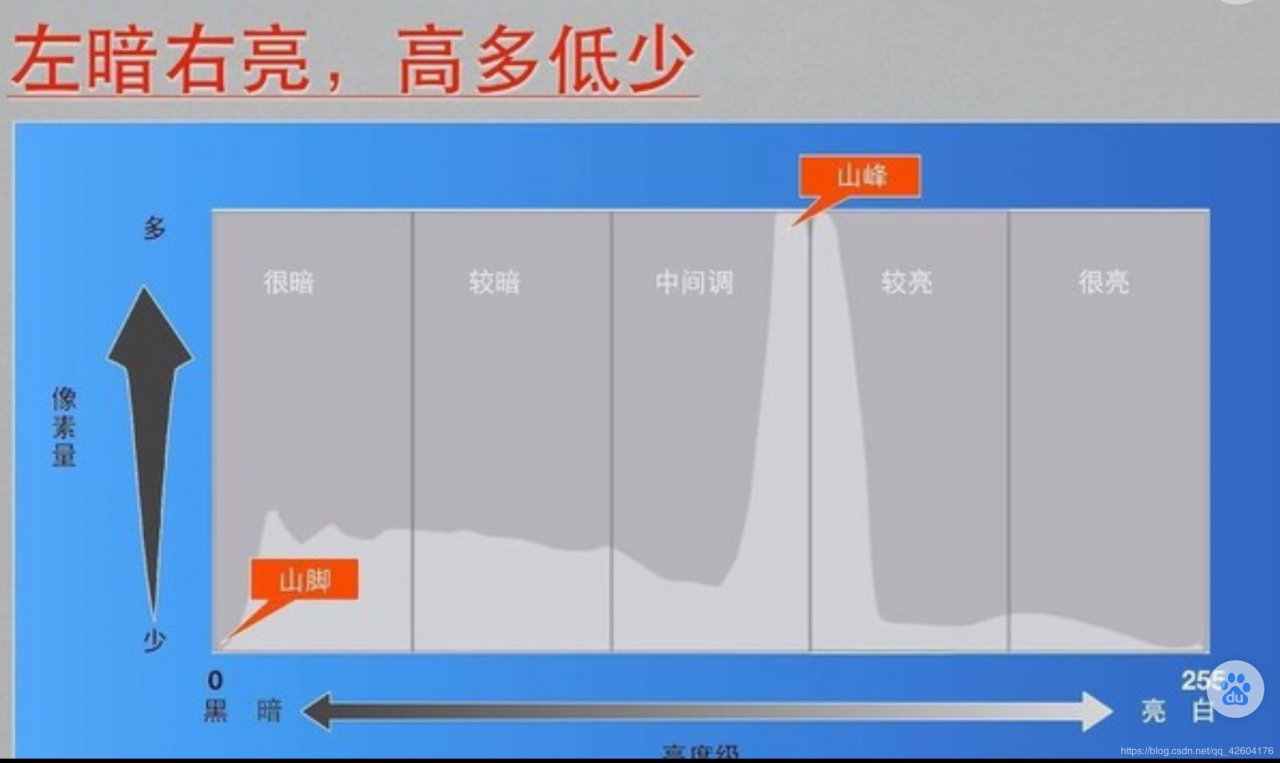
首先将灰度图转化成灰度直方图,横坐标是灰度值(0-255),纵坐标是像素个数。
如下图所示:
灰度直方图性质:
两幅灰度直方图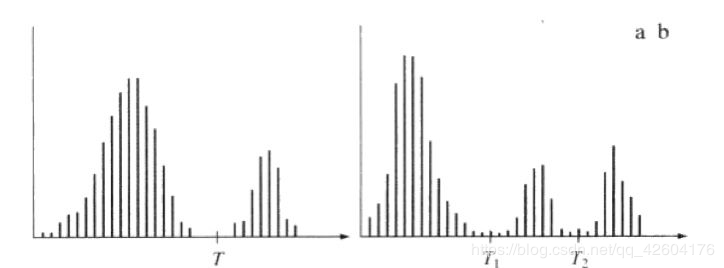
如图,从图A可以看出,直方图有两个明显的波峰和一个明显的波谷,表明灰度普遍分为两个密集区域。此时将门限设置在两者之间的波谷,则可以很好地分割出背景和物体。
同理,观察图B,有三个明显的波峰和两个明显的波谷,此时可以设置双门限,将图像分割为三类,如下图冰山就是很好的例子,分割为暗背景、冰山的明亮区域和阴影区域。
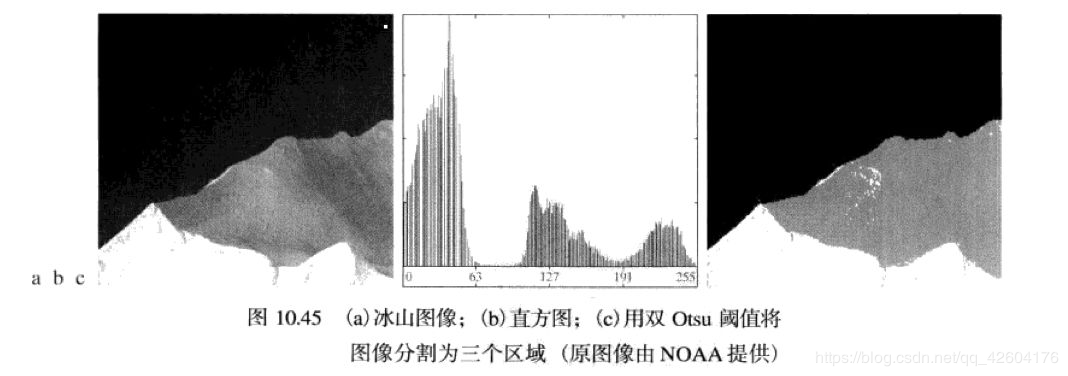
然而并不是所有图像的直方图都是有明显的多个波峰和波谷的。
单峰型:
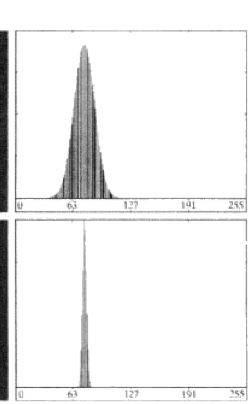
无明显波谷型
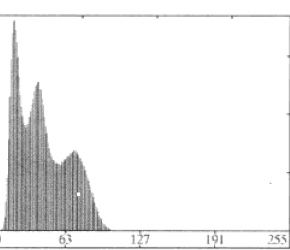
灰度趋于一致型(被噪声污染过)
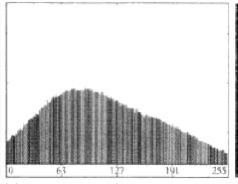
灰度阈值取决于波谷的宽度和深度,影响波谷特性的关键因素有:
1、波峰的间隔(波峰离得越远,分离这些模式机会越好)
2、图像中的噪声内容(模式随噪声的增加而展宽)
3、物体和背景的相对尺寸
4、光源的均匀性
5、图像反射的均匀性
接下来的所有的阈值处理方法,其目的都是:将灰度直方图变得好处理 并 找到分割背景和物体的门限灰度值。
基于全局的阈值处理 1迭代算法算法步骤:


粗略的代码实现:(没用过)
#define H 185
#define W 70
void Iteration(byte T,byte delta_T)
{
//分割图像
byte i,j;
float m1=0;
float m2=0;
byte old_T=T;
byte new_T=0.5*(m1+m2);
while(abs(new_T-old_T)>delta_T)
{
int G1=0;
int G2=0;
int timer_G1=0;
int timer_G2=0;
for(i=0;i<H;i++)
{
for(j=0;jT)
{
G1+=arry[i][j];
timer_G1++;
}
else
{
G2+=arry[i][j];
timer_G2++;
}
}
}
m1=G1*1.0f/timer_G1;
m2=G2*1.0f/timer_G2;
old_T=new_T;
new_T=0.5*(m1+m2);
}
//根据得出的阈值二值化图像
for(i=0;i<H;i++)
{
for(j=0;jnew_T)
{
arry[i][j]=255;
}
else
{
arry[i][j]=0;
}
}
}
}
当直方图存在比较明显的波谷时,这种方法是比较好的。δT控制迭代次数,此处我用的是byte类型的,没有小数,对精度有影响的。
这是

大津法又叫最大类间方差法、最大类间阈值法(OTSU)。
它的基本思想是,用一个阈值将图像中的数据分为两类,
一类中图像的像素点的灰度均小于这个阈值,另一类中的图像的像素点的灰度均大于或者等于该阈值。 //一般来说使用遍历的方法来求
如果这两个类中像素点的灰度的方差越大,说明获取到的阈值就是最佳的阈值
(方差是灰度分布均匀性的一种度量,背景和前景之间的类间方差越大,说明构成图像的两部分的差别越大,当部分前景错分为背景或部分背景错分为前景都会导致两部分差别变小。因此,使类间方差最大的分割意味着错分概率最小。)。
则利用该阈值可以将图像分为前景和背景两个部分。
而我们所感兴趣的部分一般为前景。
对于灰度分布直方图有两个峰值的图像,大津法求得的T近似等于两个峰值之间的低谷。
(这段阐述转自这里https://www.jianshu.com/p/56b140f9535a)
从一篇博客截来的图,罗列了我们要计算的变量。https://blog.csdn.net/u012198575/article/details/81128799

粗略代码实现
#define H 186
#define W 70
byte Ostu()
{
byte Ostu_Threshold = 0; //大津阈值
int size=H*W;
float variance; //类间方差
float maxVariance = 0, w1 = 0, w2 = 0, avgValue = 0;
float u0=0,u1=0,u2=0;
//生成灰度直方图
float histogram[256]; //灰度直方图
byte i,j;
for(i=0;i<H;i++)
{
for(j=0lj<W;j++)
{
histogram[arry[i][j]]++;
}
}
for(i=0;i<=255;i++)
{
//对直方图归一化
histogram[i]=histogram[i]/size; //代表灰度值为i像素占整个处理图像的百分比
}
//遍历找出类间方差最大(maxVariance)的阈值(Ostu_Threshold)
for(i=0;i<=255;i++)
{
//计算背景像素占比,平均灰度
for(j=0;j<=i;j++)
{
w1+=histogram[j];
u1+=histogram[j]*j;
}
//计算前景像素占比,平均灰度
w2=1-w1;
if(i==255)
{
u2=histogram[j]*j;
}
else
{
for(j=i+1;j maxVariance)
{ //找到使灰度差最大的值
maxVariance = variance;
Ostu_Threshold = i; //那个值就是阈值
}
}
return Ostu_Threshold;
}
3用图像平滑改善全局阈值处理
总的来说就是在二值化之前先用33或者55之类的均值模板将整个图像处理一下。
不过这样的坏处是使物体与背景的边界变得有些模糊。侵蚀越多,边界误差越大。
在某些极端情况下,这种方法效果并不好。
这种方法将关注聚焦于物体与背景的边缘像素,在边缘的灰度跳动非常明显,由此得到的灰度直方图将会得到很大的改善。
在这里我们求得边缘的方法主要是梯度算子和拉普拉斯算子。
算法步骤:

一般来说我们确定阈值T是根据,梯度最大值或者拉普拉斯最大值的某百分比来确定的。当有不同需求时,采用不同的占比。
这种阈值处理的目的是为了解决光照和反射带来的问题。
1图像分块可变阈值处理其实就是把一个图片分割为多块,分别使用大津阈值。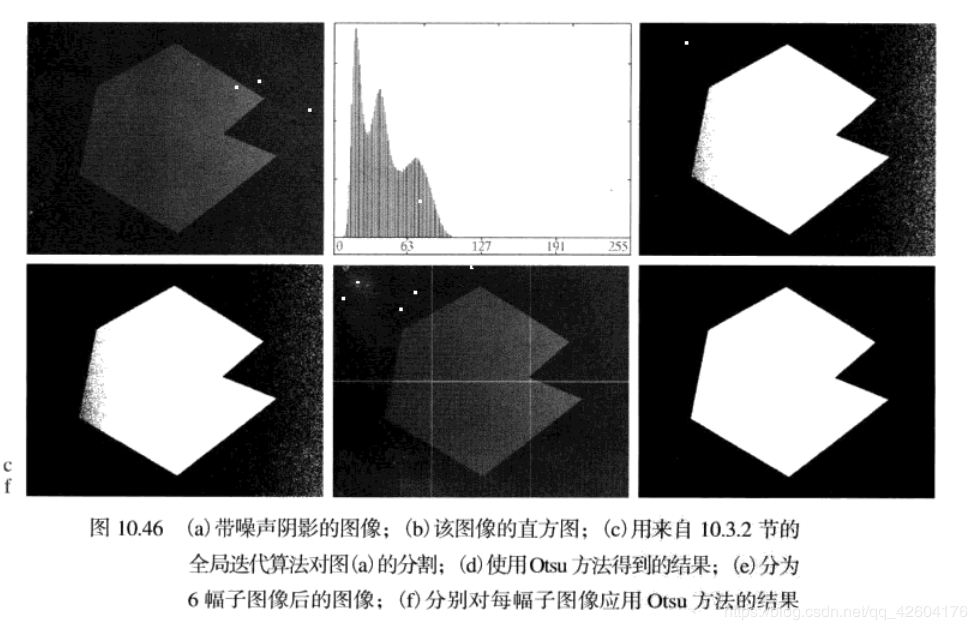
分块处理后的子图像直方图

算法步骤:
1、计算以某一像素为中心的邻域的灰度标准差和均值

2、设定可变阈值
3、观察是否满足阈值条件
4、二值化

其中a和b都是需要人工整定。
效果图:
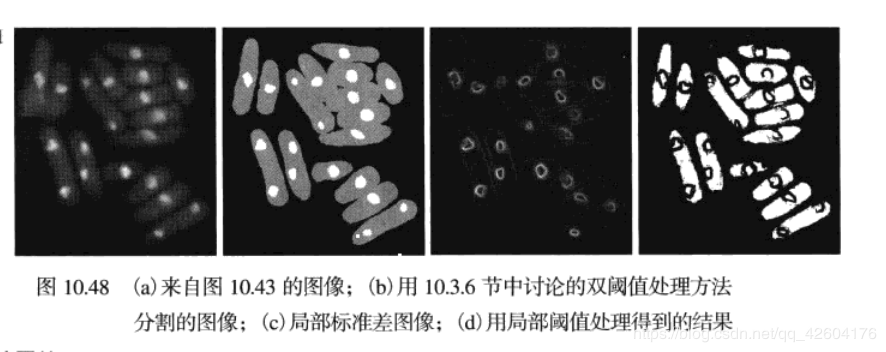

有关的链接:(这个算法我还没有理解,等我理解了再来补充)
https://blog.csdn.net/qq_34510308/article/details/93162142
作者:狄傻狗