二分图算法总结(染色法、匈牙利算法)
二分图: 所有的点可以分为两个集合V1、V2,图中任意一条边的两个顶点分别在不同的集合,即任意一个集合的内部不能有边。
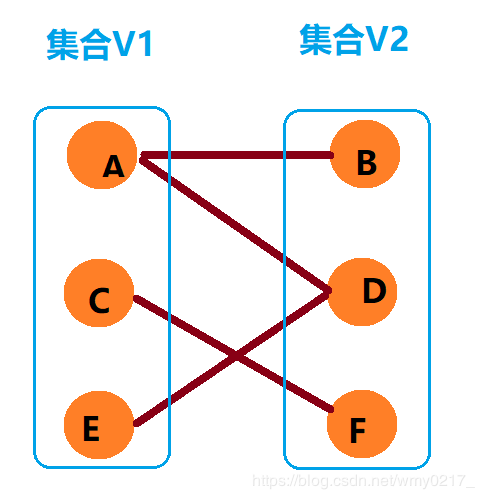
二分图中不含奇数环(奇数环: 边数为奇数的环)
解释一下! 如下图:) 如果 A 放到 V1 集合,B 放到 V2 集合,那么 C 应该放到哪个集合呢,很明显,C 与 A、B 都有边,放哪个集合都不行!!!

1、我们这里将 1 和 2 代表两种颜色(也就是两个集合,染1的在一个集合,染2的在另一个集合),初始时所有点颜色都为0,代表未染色。
2、默认将第一个点染成 1 (默认为2也可以)
3、再 dfs/bfs 对其他点进行染色
4、至少有两个邻接点染色相同,则染色失败,(邻接点染相同颜色的话,说明这两个点在同一集合,而二分图是不能有邻接点在同一集合的)不是二分图,否则就是二分图
① 默认将 A 染成 1
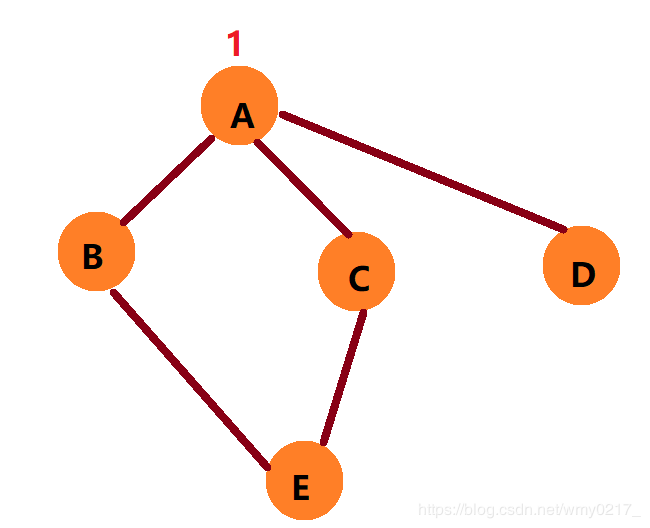
② 那么 B、C、D 只能染 2
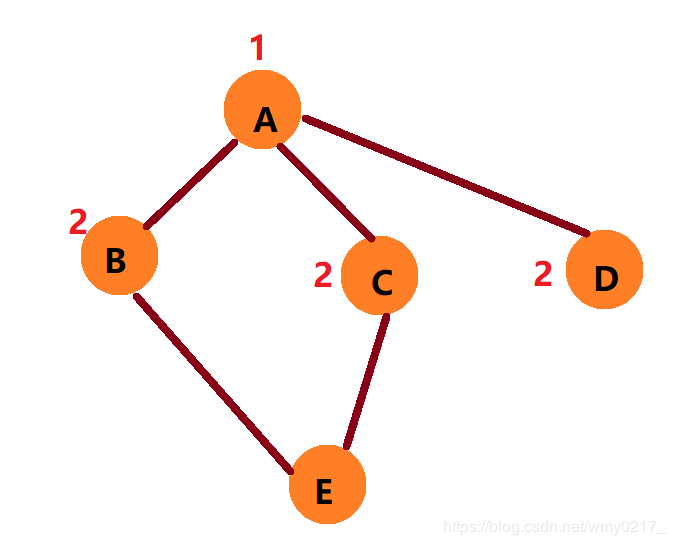
③ E 只能染 1
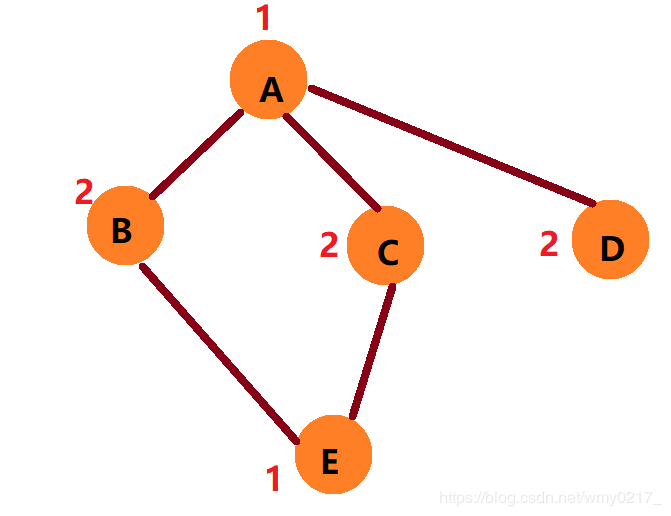
④ 所有点均被染色,并且没有出现两个邻接点是同一颜色,说明此图是二分图
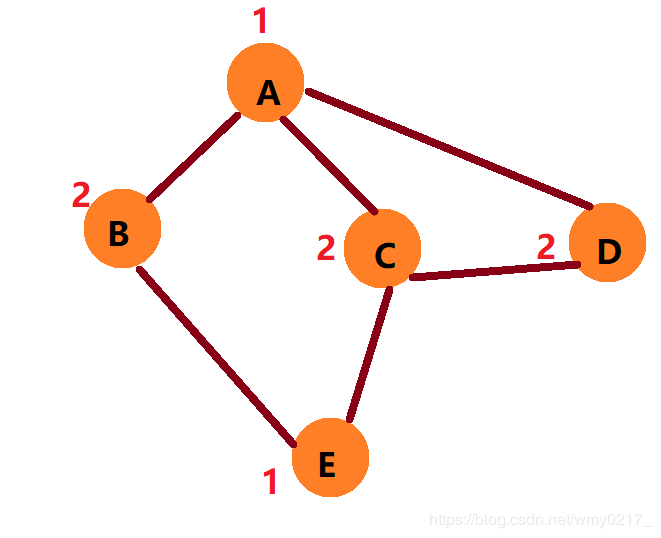
如果在这个图的基础上,我们加一条边,如下图,C 和 D是邻接点染了相同颜色,证明不是二分图
例题: AcWing 860. 染色法判定二分图
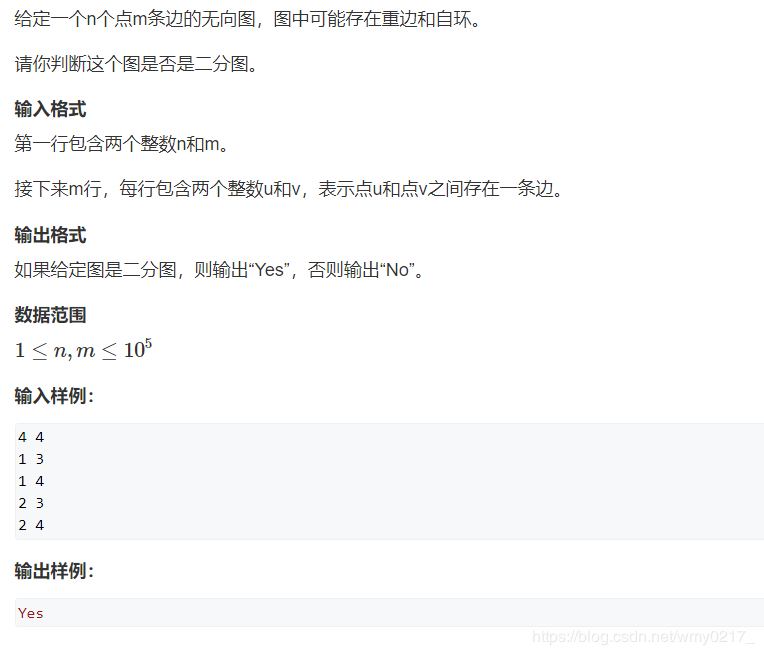
dfs做法:
#include
#include
#include
using namespace std;
const int N = 1e5+10, M = 2e5+10;
int n,m;
int h[N], e[M], ne[M], idx; //邻接表的存储
int color[N];
void add(int a,int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool dfs(int u,int c)
{
color[u] = c; //当前这个点u的颜色是 c
for(int i=h[u]; i!=-1; i=ne[i])
{
int j = e[i];
if(!color[j]) //u 的邻接点 j 未被染色
{
dfs(j,3-c); // u的颜色如果是1,j就是3-1=2;u的颜色如果是2,j就是3-2=1
}
else if(color[j] == c) return false; //两邻接点染相同颜色
}
return true;
}
int main()
{
cin >> n >> m;
memset(h,-1,sizeof(h));
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b), add(b,a); // 无向图建两条相反方向的边
}
bool flag = true;
for(int i=1; i<=n; i++) //遍历图的所有点
if(!color[i])
{
if(!dfs(i,1))
{
flag = false;
break;
}
}
if(flag) cout<<"Yes";
else cout<<"No";
}
bfs做法:
#include
#include
#include
#include
using namespace std;
typedef pair PII; //first存点编号,second存颜色
const int N = 1e5+10, M = 2e5+10;
int n,m;
int h[N], e[M], ne[M], idx; //邻接表的存储
int color[N];
void add(int a,int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool bfs(int u)
{
queue q;
q.push({u,1});
color[u] = 1; //当前这个点u的颜色是 c
while(q.size()) //队列不空
{
PII t = q.front();
q.pop();
int ver = t.first, c = t.second;
for(int i = h[ver]; i!=-1; i=ne[i])
{
int j = e[i];
if(!color[j]) //未被染色
{
color[j] = 3 - c;
q.push({j,3-c});
}
else if(color[j] == c) return false; //两邻接点染相同颜色
}
}
return true;
}
int main()
{
cin >> n >> m;
memset(h,-1,sizeof(h));
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b), add(b,a); // 无向图建两条相反方向的边
}
bool flag = true;
for(int i=1; i<=n; i++) //遍历图的所有点
if(!color[i])
{
if(!bfs(i))
{
flag = false;
break;
}
}
if(flag) cout<<"Yes";
else cout<<"No";
}
匈牙利算法
匹配: 一个边集中的任意两条边都不依附于同一个顶点,则称这个边集是一个匹配
最大匹配: 在匹配的基础上边数最大
匈牙利算法就是求二分图的最大匹配数的。
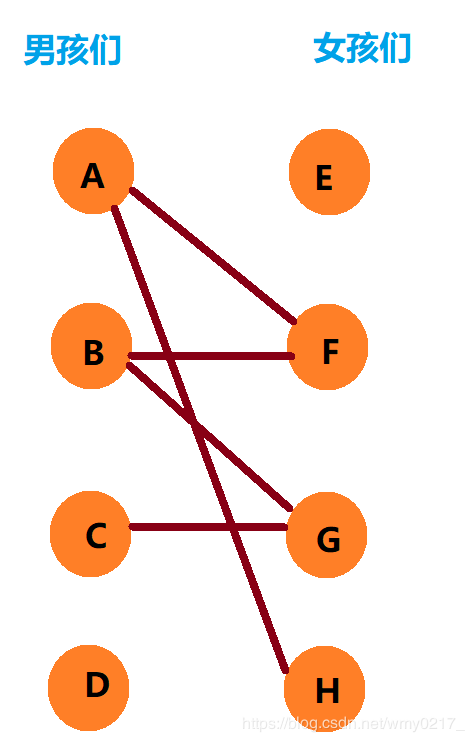
我们可以把匹配看成类似处对象一样,左边一个集合是所有男孩,右边一个集合是所有女孩,我们需要求最多可以凑成几对情侣。
下图分别是男孩和女孩,连线代表男孩喜欢的女孩(这里的女孩都比较好,只要男孩喜欢她,她就会同意在一起)。
① 首先看 A 男孩,A 男孩喜欢 F、H,且 F 单身。耶,A 和 F在一起了!
② 再看看 B 男孩,B 男孩喜欢 F、G,可 F 已经有男朋友了,但 G 没有男朋友。耶,B 和 G 在一起了!
③ 再看看 C 男孩,C 男孩只喜欢 G 女孩,可 G 已经有男朋友了,C 男孩就去找到 G 的男朋友 B,问 B 能不能换个女朋友???(B 是一个渣男,只要他还能和其他的喜欢的女生在一起,他就愿意去和现对象分手),于是,B 看了看自己除了 喜欢G,还喜欢 F ,可 F 也已经有男朋友了,B 找到了 F的男朋友 A,问 A 能不能换个女朋友(A也是渣男),A 发现自己除了 F 还喜欢 H ,很开心的与 F 分手,并与 H 在一起, 于是,B 开心的和 F 在一起了,并与 G 分手(he tui渣男) ,因为 C 男孩的坚持,C 如愿以偿的和 G 在一起了!!!
④ D 男孩可能要好好学习,不想谈恋爱,没有对象,E 女孩因为没有人喜欢,也没有对象。
所以说 ,凑成 3 对情侣(A 和 H、B 和 F、 C 和 G),最大匹配数为3.
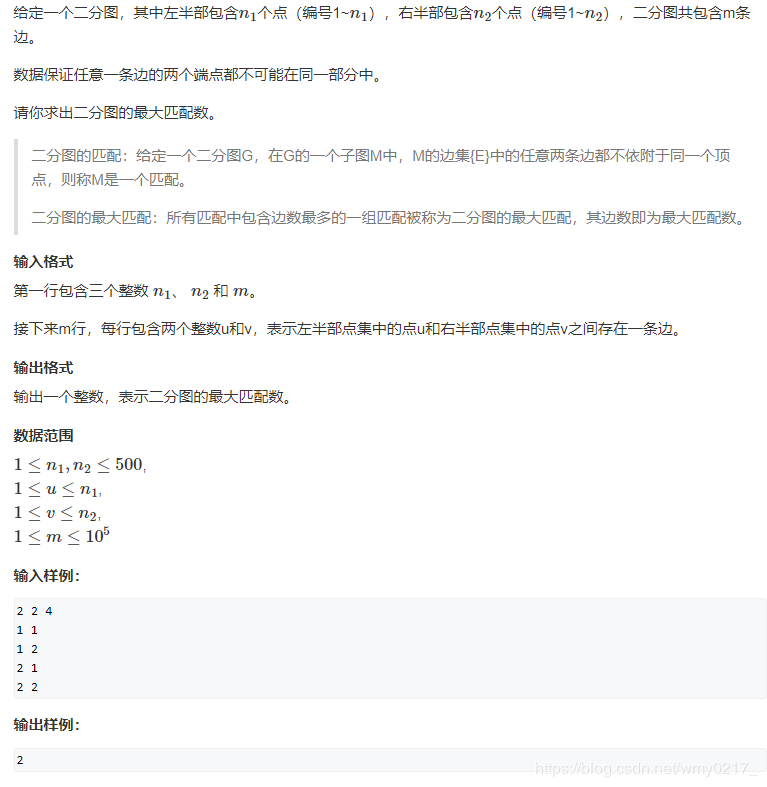
例题: AcWing 861. 二分图的最大匹配
#include
#include
#include
using namespace std;
const int N = 510,M = 1e5+10;
int n1,n2,m;
int h[N], e[M], ne[M], idx; //邻接表
int match[N];
bool st[N];
void add(int a,int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool find(int x)
{
for(int i = h[x]; i!=-1; i=ne[i]) // 遍历 x 男孩喜欢所有的女孩
{
int j = e[i];
if(!st[j]) // 如果st[j] = true 就不考虑这个女孩
{
st[j] = true; // 标记 j 这个女孩,作用是如果这个女孩有男朋友,我们去找她男朋友有没有可能和别的女孩在一起时,就不需要考虑他现对象 j 了
if(match[j] == 0 || find(match[j]))// 女孩还没有对象或女孩的男朋友可以和其他喜欢的女生在一起
{
match[j] = x; //匹配成功
return true;
}
}
}
return false;
}
int main()
{
cin >> n1 >> n2 >> m;
memset(h,-1,sizeof(h));
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b); //只存一条男生到女生的边就够用啦
}
int res = 0; // 当前匹配的数量
for(int i=1; i<=n1; i++) // 遍历每个男生
{
memset(st,false,sizeof(st)); //代表女孩还没有考虑过,每个女孩只考虑一次
if(find(i)) res++; // 男生匹配到了
}
cout << res;
}
作者:wmy0217_