统计学习方法——K近邻法(学习笔记)
K近邻法是一种基本分类与回归方法。K近邻法的输入为实例的特征向量(特征空间的点),输出为实例的类别,可以取多类。
K近邻算法假设给定一个训练数据集,其训练数据集实例的类别已定,对新的输入实例,找出新实例K个最近邻的训练点,根据K个最近邻训练实例的类别,通过多数表决等方式进行预测。
K近邻法的三个基本要素:K值的选择、距离度量、分类决策规则。
下面介绍一下kd树、搜索kd树的过程以及相关代码。
1.K近邻算法根据给定的训练数据集,对新的实例,在训练数据集中找出与该实例最近邻的K个实例,这K个实例的多数属于某类,就把输入实例分为这个类。

特征空间中两个实例点的距离是两个实例点相似程度的反映。

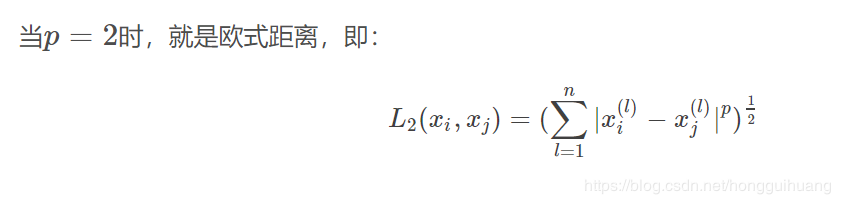
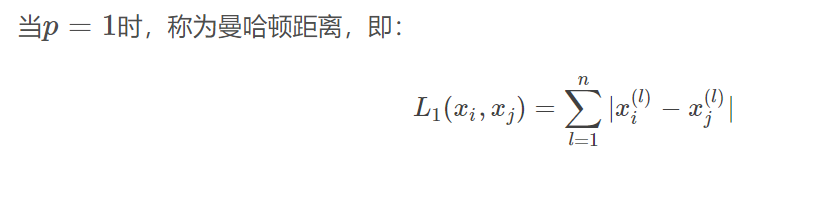
如果k值选择较小,就相当于用较小的领域中的训练实例进行预测,“学习”的近似误差会减小,只有与输入实例较近的训练实例才会对预测起作用,但确定是估计误差会增大。预测结果会对近邻的实例点非常敏感,如果近邻的实例点恰巧是噪声,预测就会出错。
如果k值选择较大,就相当于用较大的领域中的训练实例进行预测,近似误差会增大,但估计误差会减小。
特例,如果k=N,那么无论输入什么实例,都会简单的预测为训练实例中做多的类,这是的模型就没有意义了,丢失了训练实例中的大量有用信息。
这里提一下近似误差和估计误差。
近似误差和估计误差要加上Bayes误差一起理解。
Bayes误差:也叫统计误差,指的是收集统计数据的时候,由于一些极端个例的存在而造成的误差,也就是说数据是不完美的。例如: 生成的数据里面混入一个值
近似误差:Approximation Error,指的是选择的模型并不适合当前数据所造成的误差。例如:用高阶函数来近似线性数据,你可以在训练集上把误差降为0,但是当用验证集测试时,误差仍然非常大。
在K近邻法中K值越小,得出的模型越复杂,因为K值越小导致特征空间被划分成更多的子空间,对训练的预测更加准确,近似误差越小,但会出现过拟合问题。
估计误差:Estimation Error, 指的是数据集和所选择的模型确定下来后,模型拟合数据时造成的误差。最小化估计误差,即为使估计系数尽量接近真实系数,但是此时对训练样本(当前问题)得到的估计值不一定是最接近真实值的估计值;但是对模型本身来说,它能适应更多的问题(测试样本)。
k近邻法中的分类决策规则往往是多数表决,即由输入实例的k个近邻的训练实例中的多数类决定输入实例的类别。
如果分类的损失函数为0-1损失函数,则误分类的概率是:
P(Y≠f(X))=1−P(Y=f(X))P(Y≠f(X))=1−P(Y=f(X))
也就是说误分类率为:
1k∑I(yi≠cj)=1−1kI(yi=cj)1k∑I(yi≠cj)=1−1kI(yi=cj)
要使得误分类率最小,也就是经验风险最小,就要使得1kI(yi=cj)1kI(yi=cj)最大,所以多数表决规则等价于经验最小化。
5.构造kd树输入:k维空间数据集T = {x1,x2,…,xN},其中,xi=(x1(1),x2(2),…,xi(k))T,i=1,2,…,N
输出:kd树
1.构造根节点(根节点对应于包含T的K维空间的超矩形区域)
选择x(1)x(1)为坐标轴,以T中所有实例的x(1)x(1)坐标的中位数为切分点,这样,经过该切分点且垂直与x(1)x(1)的超平面就将超矩形区域切分成2个子区域。保存这个切分点为根节点。
2.重复如下步骤:
对深度为j的节点选择x(l)x(l)为切分的坐标轴,l=j(modk)+1l=j(modk)+1 ,以该节点区域中所有实例的x(l)x(l)坐标的中位数为切分点,将该节点对应的超平面切分成两个子区域。切分由通过切分点并与坐标轴x(l)x(l)垂直的超平面实现。保存这个切分点为一般节点。
3.直到两个子区域没有实例存在时停止。
直观说一下我的理解,例如训练数据集(x1,x2, … ,xn)有n个维度。先选取训练数据集第一维度的中值xi,该中值的数据作为根结点的数值。第一维度中小于中值xi的数据集作为该根结点的左孩子,大于中值xi的数据集作为该根结点右孩子。以此增加维度对第二第三到第n个维度进行递归建立kd树,直到两个子区域没有实例存在时停止。
构造kd树代码
#定义结点
def __init__(self, data, lchild = None, rchild = None):
self.data = data
self.lchild = lchild
self.rchild = rchild
#对数据集进行从小到大排序
#采用冒泡排序,利用axis作为轴进行划分
def sort(self, dataSet, axis):
sortDataSet = dataSet[ : ]
m, n = np.shape(sortDataSet)
for i in range(m - 1):
for j in range(m - i - 1):
if (sortDataSet[j][axis] > sortDataSet[j+1][axis]):
temp = sortDataSet[j]
sortDataSet[j] = sortDataSet[j+1]
sortDataSet[j+1] = temp
print(sortDataSet)
return sortDataSet
#构造kd树
def create(self, dataSet, depth): #创建Kd树返回根结点
if (len(dataSet) > 0):
m, n = np.shape(dataSet) #求出样本行,列
midIndex = int(m / 2 ) #中位数的索引位置
axis = depth % n #判断以哪个轴划分数据
sortedDataSet = self.sort(dataSet, axis) #进行排序
node = Node(sortedDataSet[midIndex])
leftDataSet = sortedDataSet[:midIndex]
rightDataSet = sortedDataSet[midIndex + 1 :]
print(leftDataSet)
print(rightDataSet)
node.lchild = self.create(leftDataSet, depth+1)
node.rchild = self.create(rightDataSet, depth+1)
return node
else:
return None
6.搜索kd树
kd树最近邻搜索算法
输入:已构造的kd树:目标点x;
输出:x的最近邻。
(1)在kd树中找出包含目标点x的叶结点:从根结点出发,递归的向下访问kd树。若目标点x当前维的坐标小于切分点的坐标,则移动到左子结点,否则移动到右子节点,直到子节点为叶结点为止。
(2)以此叶节点为“当前最近点”。
(3)递归的向上回退,在每个结点进行以下操作:
(a) 如果该结点保存的实例点比当前最近点距离目标点更近,则以该实例点为“当前最近点”。
(b) 当前最近点一定存在于该结点一个子结点对应的区域。检查该子结点的另一子结点对应的区域是否有更近的点。
具体的,检查另一子结点对应的区域是否与以目标点为球心,以目标点与“当前最近点”间的距离为半径的超球体相交。
如果相交,可能在另一个子结点对应的区域内存在距离目标点更近的点,移动到另一个子结点,接着,递归地进行最近邻搜索。
如果不相交,向上回退。
(4)当回退到根结点时,搜索结束,最后的“当前最近点”即为x的最近邻点。
直观说一下我的理解,对新实例,根据坐标找到叶节点,把叶节点最为“当前最近点”向根结点递归回去,1.对每个结点计算新实例与该结点的距离Li并与新结点与“当前最近点”的距离L对比大小,如果Li比L小,则该结点为“当前最近点”,2.看是否需要去另一子节点查找(叶节点除外)
搜索kd树代码
#求解欧氏距离
def dist(self, x1, x2):
return ((np.array(x1) - np.array(x2)) ** 2).sum() ** 0.5
#搜索Kd树
def search(self, tree, x):
self.nearestPoint = None #保存最近的点
self.nearestValue = 0 #保存最近的值
def travel(node, depth = 0): #递归搜索
if node != None: #递归终止条件
n = len(x) #特征数
axis = depth % n #计算轴
if x[axis] distNodeAndX):
self.nearestPoint = node.data
self.nearestValue = distNodeAndX
print(node.data, depth, self.nearestValue, node.data[axis], x[axis])
if (abs(x[axis] - node.data[axis]) <= self.nearestValue): #确定是否需要去子节点的区域去找(圆的判断)
if x[axis] < node.data[axis]:
travel(node.rchild, depth+1)
else:
travel(node.lchild, depth + 1)
travel(tree)
return self.nearestPoint
7.构造kd树、搜索kd树完整代码
import numpy as np
class Node:
def __init__(self, data, lchild = None, rchild = None): #定义结点
self.data = data
self.lchild = lchild
self.rchild = rchild
class KdTree:
def __init__(self):
self.kdTree = None
def create(self, dataSet, depth): #创建Kd树返回根结点
if (len(dataSet) > 0):
m, n = np.shape(dataSet) #求出样本行,列
midIndex = int(m / 2 ) #中位数的索引位置
axis = depth % n #判断以哪个轴划分数据
sortedDataSet = self.sort(dataSet, axis) #进行排序
node = Node(sortedDataSet[midIndex])
leftDataSet = sortedDataSet[:midIndex]
rightDataSet = sortedDataSet[midIndex + 1 :]
print(leftDataSet)
print(rightDataSet)
node.lchild = self.create(leftDataSet, depth+1)
node.rchild = self.create(rightDataSet, depth+1)
return node
else:
return None
def sort(self, dataSet, axis): #采用冒泡排序,利用axis作为轴进行划分
sortDataSet = dataSet[ : ]
m, n = np.shape(sortDataSet)
for i in range(m - 1):
for j in range(m - i - 1):
if (sortDataSet[j][axis] > sortDataSet[j+1][axis]):
temp = sortDataSet[j]
sortDataSet[j] = sortDataSet[j+1]
sortDataSet[j+1] = temp
print(sortDataSet)
return sortDataSet
def preOrder(self, node):
if node !=None:
print("tttt->%s" % node.data)
self.preOrder(node.lchild)
self.preOrder(node.rchild)
def search(self, tree, x):
self.nearestPoint = None #保存最近的点
self.nearestValue = 0 #保存最近的值
def travel(node, depth = 0): #递归搜索
if node != None: #递归终止条件
n = len(x) #特征数
axis = depth % n #计算轴
if x[axis] distNodeAndX):
self.nearestPoint = node.data
self.nearestValue = distNodeAndX
print(node.data, depth, self.nearestValue, node.data[axis], x[axis])
if (abs(x[axis] - node.data[axis]) <= self.nearestValue): #确定是否需要去子节点的区域去找(圆的判断)
if x[axis] < node.data[axis]:
travel(node.rchild, depth+1)
else:
travel(node.lchild, depth + 1)
travel(tree)
return self.nearestPoint
def dist(self, x1, x2):
return ((np.array(x1) - np.array(x2)) ** 2).sum() ** 0.5
dataSet = [[2, 3],
[5, 4],
[9, 6],
[4, 7],
[8, 1],
[7, 2]]
x = [5, 3]
kdtree = KdTree()
tree = kdtree.create(dataSet, 0)
kdtree.preOrder(tree)
print(kdtree.search(tree, x))
输出

作者:hongguihuang