梯度下降算法和牛顿算法原理以及使用python用梯度下降和最小二乘算法求回归系数
梯度下降算法
以下内容参考 微信公众号 AI学习与实践平台 SIGAI
导度和梯度的问题
因为我们做的是多元函数的极值求解问题,所以我们直接讨论多元函数。多元函数的梯度定义为:
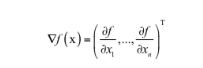
其中称为梯度算子,它作用于一个多元函数,得到一个向量。下面是计算函数梯度的一个例子
![]()
可导函数在某一点处取得极值的必要条件是梯度为0,梯度为0的点称为函数的驻点,这是疑似极值点。需要注意的是,梯度为0只是函数取极值的必要条件而不是充分条件,即梯度为0的点可能不是极值点。
至于是极大值还是极小值,要看二阶导数/Hessian矩阵,Hessian矩阵我们将在后面的文章中介绍,这是由函数的二阶偏导数构成的矩阵。这分为下面几种情况:
如果Hessian矩阵正定,函数有极小值
如果Hessian矩阵负定,函数有极大值
如果Hessian矩阵不定,则需要进一步讨论
这和一元函数的结果类似,Hessian矩阵可以看做是一元函数的二阶导数对多元函数的推广。一元函数的极值判别法为,假设在某点处导数等于0,则:
如果二阶导数大于0,函数有极小值
如果二阶导数小于0,函数有极大值
如果二阶导数等于0,情况不定
精确的求解不太可能,因此只能求近似解,这称为数值计算。工程上实现时通常采用的是迭代法,它从一个初始点 x(0) 开始,反复使用某种规则从x(k) 移动到下一个点x(k+1),构造这样一个数列,直到收敛到梯度为0的点处。即有下面的极限成立:
![]()
这些规则一般会利用一阶导数信息即梯度;或者二阶导数信息即Hessian矩阵。这样迭代法的核心是得到这样的由上一个点确定下一个点的迭代公式:
![]()
这个过程就像我们处于山上的某一位置,要到山下去,因此我们必须到达最低点处。此时我们没有全局信息,根本就不知道哪里是地势最低的点,只能想办法往山下走,走 一步看一步。刚开始我们在山上的某一点处,每一步,我们都往地势更低的点走,以期望能走到山底。
最后我们来看一下梯度算法的推导过程。
多元函数f(x) 在x点处的泰勒展开为
![]()
这里我们忽略了二次及更高的项。其中,一次项是梯度向量与自变量增量Δx 的内积,这等价于一元函数的f`(x0) Δx 。这样,函数的增量与自变量的增量Δx ,函数梯度的关系可以表示为:
![]()
如果 Δx 足够小,在x的某一邻域内,则我们可以忽略二次及以上的项,有:
![]()
这里的情况比一元函数复杂多了, Δx 是一个向量,Δx有无穷多种方向,该往哪个方向走呢?如果能保证:
![]()
就可以得到
![]()
即函数值递减,这就是下山的正确方向。因为有:
![]()
因为向量的模一定大于等于0,如果:
![]()
就能保证
![]()
即选择合适的增量 Δx ,就能保证函数值下降,要达到这一目的,只要保证梯度和 Δx的夹角的余弦值小于等于0就可以了。由于有:
![]()
只有当θ=π的时候,cosθ有极小值-1,此时梯度和 Δx反向,即夹角为180度。因此当向量 Δx的模大小一定时,当
![]()
即在梯度相反的方向函数值下降的最快。此时有:cosθ= -1
函数的下降值为:
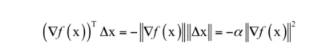
只要梯度不为0,往梯度的反方向走函数值一定是下降的。直接用可能会有问题,因为x+ Δx 可能会超出x的邻域范围之外,此时是不能忽略泰勒展开中的二次及以上的项的,因此步伐不能太大。一般设:
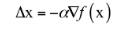
其中α 为一个接近于0的正数,称为步长,由人工设定,用于保证x+ Δx 在x的邻域内,从而可以忽略泰勒展开中二次及更高的项,则有:
![]()
从初始点x(0) 开始,使用如下迭代公式:
![]()
只要没有到达梯度为0的点,则函数值会沿着序列x(k) 递减,最终会收敛到梯度为0的点,这就是梯度下降法。迭代终止的条件是函数的梯度值为0(实际实现时是接近于0),此时认为已经达到极值点。
牛顿算法的原理
在最优化的问题中,线性最优化至少可以使用单纯行法求解,但对于非线性优化问题,牛顿法提供了一种求解的办法。假设任务是优化一个目标函数f,求函数f的极大极小问题,可以转化为求解函数f的导数f’=0的问题,这样求可以把优化问题看成方程求解问题(f’=0)。
为了求解f’=0的根,把f(x)的泰勒展开,展开到2阶形式:
![]()
这个式子是成立的,当且仅当 Δx 无线趋近于0。此时上式等价与:
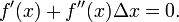
求解:
![]()
得出迭代公式:
![]()
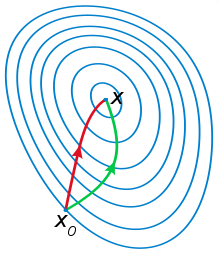
一般认为牛顿法可以利用到曲线本身的信息,比梯度下降法更容易收敛(迭代更少次数),如下图是一个最小化一个目标方程的例子,红色曲线是利用牛顿法迭代求解,绿色曲线是利用梯度下降法求解。
牛顿法原理参考以下链接:
原文链接:https://blog.csdn.net/a819825294/article/details/52172463
下面我们来用梯度下降法来求解下面这个式子的极小值和极小点
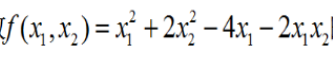
首先我们用Excel来计算。
用Excel只需要注意对x1和x2求偏导的计算公式就基本不会出错。
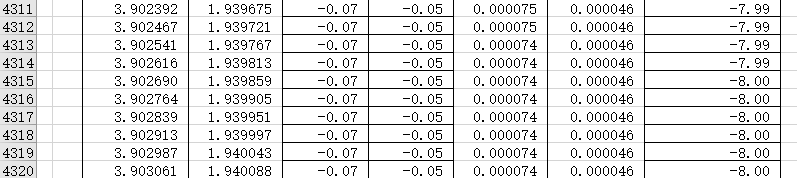
可以看到虽然函数值在4315就达到了极小值,但是x1和x2的值还是在微小变化,这时候我们一定要求到x1和x2的值不再变化。这样才是收敛。

到这里才几乎没有变化了。
然后我们用python代码来实现梯度下降
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
from mpl_toolkits.mplot3d import Axes3D
import warnings
# 二维原始图像
def f2(x1, x2):
return x1**2 + 2*x2**2 - 4*x1 - 2*x1*x2
## 偏函数
def hx1(x1, x2):
return 2*x1 - 4 -2*x2
def hx2(x, y):
return 4*x2-2*x1
x1 = 4
x2 = 2
alpha = 0.001
#保存梯度下降经过的点
GD_X1 = [x1]
GD_X2 = [x2]
GD_Y = [f2(x1,x2)]
# 定义y的变化量和迭代次数
y_change = f2(x1,x2)
iter_num = 1
while(y_change > 1e-10 and iter_num < 100) :
tmp_x1 = x1 - alpha * hx1(x1,x2)
tmp_x2 = x2 - alpha * hx2(x1,x2)
tmp_y = f2(tmp_x1,tmp_x2)
f_change = np.absolute(tmp_y - f2(x1,x2))
x1 = tmp_x1
x2 = tmp_x2
GD_X1.append(x1)
GD_X2.append(x2)
GD_Y.append(tmp_y)
iter_num += 1
print("极值点" ,(x1, x2))
print("极值" ,f2(x1,x2))
print(GD_X1)
print(GD_X2)
极值点 (4, 2)
极值 -8
[4]
[2]
可以看到其实前面Excel的结果还是有一点点出入的,但是大致上是相同的。
下面我们用梯度下降算法求解漫画书中“店铺多元回归”的问题,漫画中数据如下
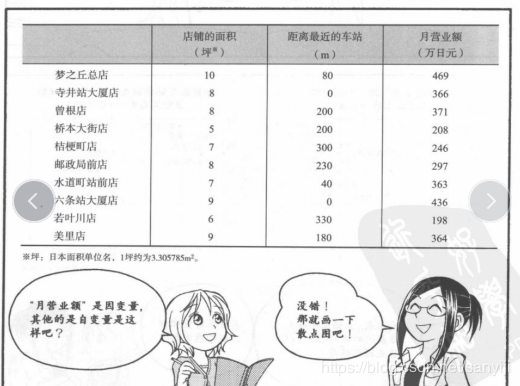
我们把这些数据写入Excel,然后保存为csv格式:
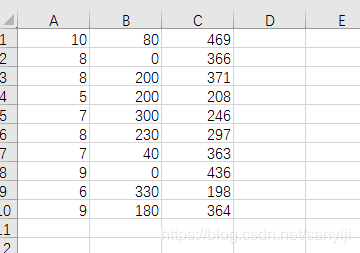
然后用前面的csv文件在python中用梯度算法求解回归系数
代码如下
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
data=np.genfromtxt('营业额.csv',delimiter=',')
x_data=data[:,:-1]
y_data=data[:,2]
#定义学习率、斜率、截据
#设方程为y=theta1x1+theta2x2+theta0
lr=0.00001
theta0=0
theta1=0
theta2=0
#定义最大迭代次数,因为梯度下降法是在不断迭代更新k与b
epochs=10000
#定义最小二乘法函数-损失函数(代价函数)
def compute_error(theta0,theta1,theta2,x_data,y_data):
totalerror=0
for i in range(0,len(x_data)):#定义一共有多少样本点
totalerror=totalerror+(y_data[i]-(theta1*x_data[i,0]+theta2*x_data[i,1]+theta0))**2
return totalerror/float(len(x_data))/2
#梯度下降算法求解参数
def gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs):
m=len(x_data)
for i in range(epochs):
theta0_grad=0
theta1_grad=0
theta2_grad=0
for j in range(0,m):
theta0_grad-=(1/m)*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta2)+y_data[j])
theta1_grad-=(1/m)*x_data[j,0]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
theta2_grad-=(1/m)*x_data[j,1]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
theta0=theta0-lr*theta0_grad
theta1=theta1-lr*theta1_grad
theta2=theta2-lr*theta2_grad
return theta0,theta1,theta2
#进行迭代求解
theta0,theta1,theta2=gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs)
#print('结果:迭代次数:{0} 学习率:{1}之后 a0={2},a1={3},a2={4},代价函数为{5}'.format(epochs,lr,theta0,theta1,theta2,compute_error(theta0,theta1,theta2,x_data,y_data)))
print("多元线性回归方程为:y=",theta1,"X1+",theta2,"X2+",theta0)
#画图
ax=plt.figure().add_subplot(111,projection='3d')
ax.scatter(x_data[:,0],x_data[:,1],y_data,c='r',marker='o')
x0=x_data[:,0]
x1=x_data[:,1]
#生成网格矩阵
x0,x1=np.meshgrid(x0,x1)
z=theta0+theta1*x0+theta2*x1
#画3d图
ax.plot_surface(x0,x1,z)
ax.set_xlabel('area')
ax.set_ylabel('distance')
ax.set_zlabel("Monthly turnover")
plt.show()
多元线性回归方程为:y= 45.0533119768975 X1+ -0.19626929358281256 X2+ 5.3774162274868
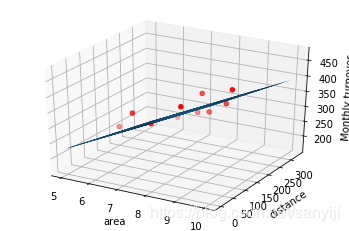
之前我用最小二乘法计算过店铺的回归系数
代码如下:
#导模块
import numpy as np
import pandas as pd
#变量初始化
X=[]
Y=[]
B=[]
Q_e=0
Q_E=0
#从csv文件中读取数据
def get_data(file_name):
data=pd.read_csv(file_name,header=0)
data=np.array(data)
Y=data[:,data.shape[1]-1]#预测对象位于最后一列
X=data[:,0:data.shape[1]-1]
print(X.shape)
return X,Y
return X,Y
X,Y=get_data('salary.csv')
X=np.mat(np.c_[np.ones(X.shape[0]),X])#为系数矩阵增加常数项系数
Y=np.mat(Y)#数组转化为矩阵
B=np.linalg.inv(X.T*X)*(X.T)*(Y.T)
print("第一项为常数项,其他为回归系数",B)#输出系数,第一项为常数项,其他为回归系数
print("输入店铺面积,距离最近的车站距离,预测营业额:",np.mat([1,10,80])*B ,"万日元")#预测结果
#相关系数
Y_mean=np.mean(Y)
for i in range(Y.size):
Q_e+=pow(np.array((Y.T)[i]-X[i]*B),2)
Q_E+=pow(np.array(X[i]*B)-Y_mean,2)
R2=Q_E/(Q_e+Q_E)
print("R2的值:",R2)
(10, 2)
第一项为常数项,其他为回归系数 [[65.32391639]
[41.51347826]
[-0.34088269]]
输入店铺面积,距离最近的车站距离,预测营业额: [[453.1880841]] 万日元
R2的值: [[0.94523585]]
再看Excel的结果
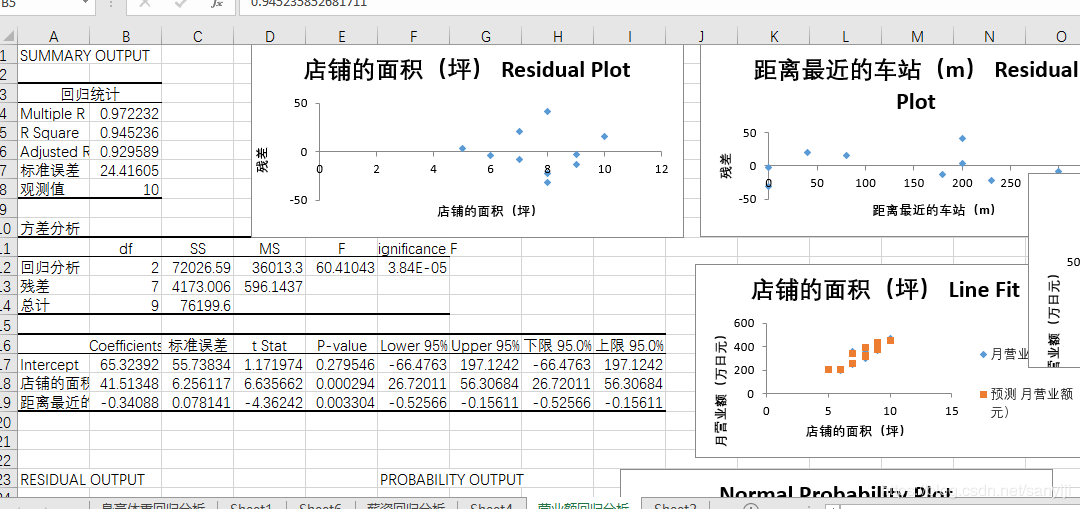
可以看到我们用最小二乘法得到的结果和Excel做回归分析得到的结果一致,而用梯度下降法得到的却和这两个方法有所差异。
作者:sanyiji