Task2:EDA之数字特征分析
数字特征分析包含:相关性分析、查看几个特征的偏度和峰值、每个数字特征的分布可视化、数字特征相互之间的关系可视化、多变量互相回归关系可视化这五个部分。
进行数字特征分析之前,我们需要先安装基础工具、载入数据、定义数字特征。
本文中使用的数据来自天池大赛,零基础入门数据挖掘 - 二手车交易价格预测,地址:https://tianchi.aliyun.com/competition/entrance/231784/information
#coding:utf-8
#导入warnings包,利用过滤器来实现忽略警告语句。
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
##载入训练集和测试集;
Train_data = pd.read_csv('used_car_train_20200313.csv', sep=' ')
Test_data = pd.read_csv('used_car_testA_20200313.csv', sep=' ')
# 分离label即预测值,人为定义数字特征
Y_train = Train_data['price']
numeric_features = ['power', 'kilometer', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4','v_5', 'v_6', 'v_7', 'v_8','v_9', 'v_10', 'v_11','v_12', 'v_13', 'v_14']
一、相关性分析
代码##计算相关系数
numeric_features.append('price')
price_numeric = Train_data[numeric_features]
correlation = price_numeric.corr()
print(correlation['price'].sort_values(ascending = False),'\n')
##画热力图
f , ax = plt.subplots(figsize = (7, 7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation,square = True, vmax=0.8)
del price_numeric['price']
结果如下:
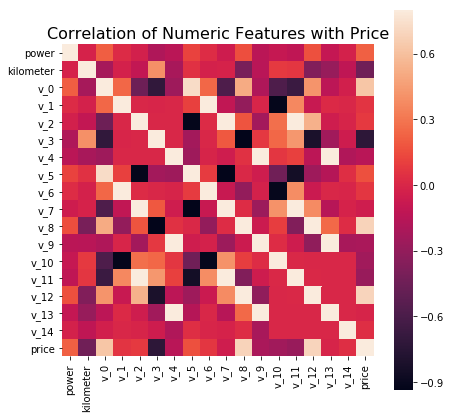
相关系数表对每个特征与price的相关性排了个序。可以看出二手汽车的价格price与v_12、v_8、v_0、power、v_5、v_2、v_6、v_1、v_14特征成正相关,且其中v_12、v_8、v_0与price相关性较为显著;price与v_13、v_7、v_4、v_9、v_10、v_11、kilometer、v_3特征成负相关,且其中v_3与price相关性较为显著。
二、偏度和峰值
代码## 查看几个特征得 偏度和峰值
for col in numeric_features:
print('{:15}'.format(col),
'Skewness: {:05.2f}'.format(Train_data[col].skew()) ,
' ' ,
'Kurtosis: {:06.2f}'.format(Train_data[col].kurt())
)
结果如下: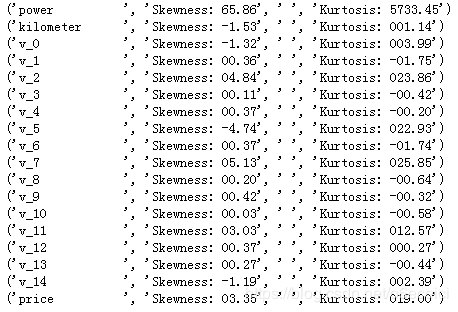
三、分布可视化
代码##每个数字特征得分布可视化
f = pd.melt(Train_data, value_vars=numeric_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False)
g = g.map(sns.distplot, "value")
结果如下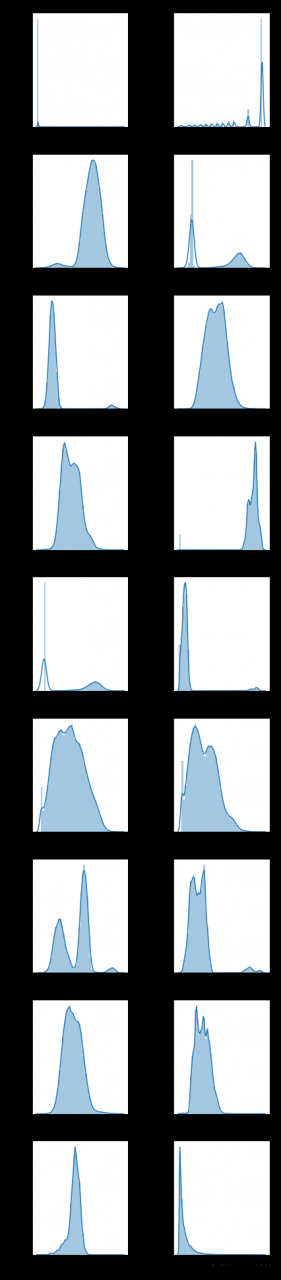
由可视化图可以看出,power特征和kilometer特征的分布在某个区间较为密集;v_0-v_14匿名特征分布较为均匀。
四、数字特征相互之间的关系可视化
代码##数字特征相互之间的关系可视化
sns.set()
columns = ['price', 'v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']
sns.pairplot(Train_data[columns],size = 2 ,kind ='scatter',diag_kind='kde')
plt.show()
结果如下: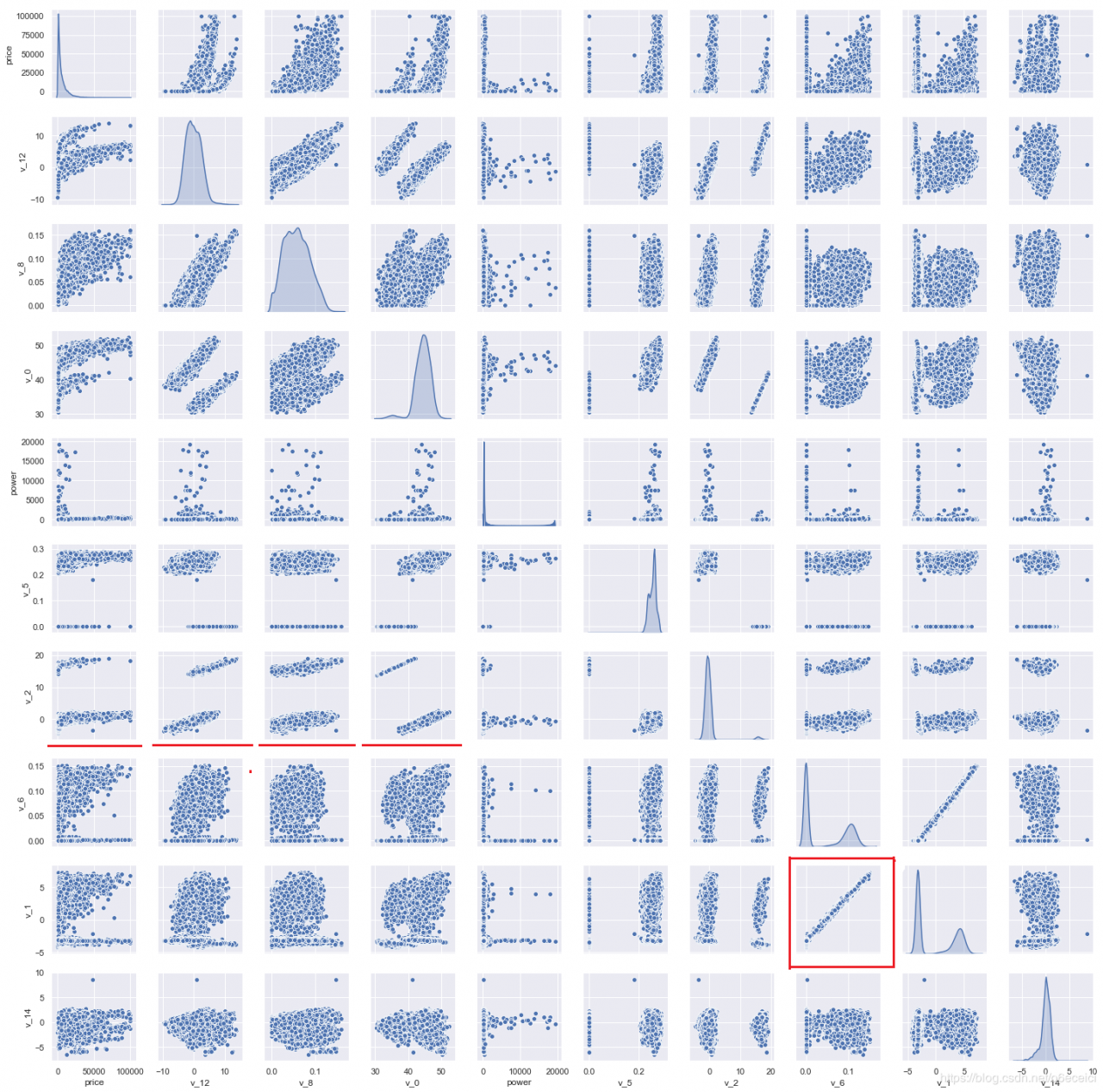
可以看到,v_1和v_6存在显著的线性关系。v_2与price,v_2与v_12,v_2与v_8,v_2与v_0呈现出一定的正相关。
五、多变量互相回归关系可视化
代码##多变量互相回归关系可视化
fig, ((ax1, ax2), (ax3, ax4), (ax5, ax6), (ax7, ax8), (ax9, ax10)) = plt.subplots(nrows=5, ncols=2, figsize=(24, 20))
v_12_scatter_plot = pd.concat([Y_train,Train_data['v_12']],axis = 1)
sns.regplot(x='v_12',y = 'price', data = v_12_scatter_plot,scatter= True, fit_reg=True, ax=ax1)
v_8_scatter_plot = pd.concat([Y_train,Train_data['v_8']],axis = 1)
sns.regplot(x='v_8',y = 'price',data = v_8_scatter_plot,scatter= True, fit_reg=True, ax=ax2)
v_0_scatter_plot = pd.concat([Y_train,Train_data['v_0']],axis = 1)
sns.regplot(x='v_0',y = 'price',data = v_0_scatter_plot,scatter= True, fit_reg=True, ax=ax3)
power_scatter_plot = pd.concat([Y_train,Train_data['power']],axis = 1)
sns.regplot(x='power',y = 'price',data = power_scatter_plot,scatter= True, fit_reg=True, ax=ax4)
v_5_scatter_plot = pd.concat([Y_train,Train_data['v_5']],axis = 1)
sns.regplot(x='v_5',y = 'price',data = v_5_scatter_plot,scatter= True, fit_reg=True, ax=ax5)
v_2_scatter_plot = pd.concat([Y_train,Train_data['v_2']],axis = 1)
sns.regplot(x='v_2',y = 'price',data = v_2_scatter_plot,scatter= True, fit_reg=True, ax=ax6)
v_6_scatter_plot = pd.concat([Y_train,Train_data['v_6']],axis = 1)
sns.regplot(x='v_6',y = 'price',data = v_6_scatter_plot,scatter= True, fit_reg=True, ax=ax7)
v_1_scatter_plot = pd.concat([Y_train,Train_data['v_1']],axis = 1)
sns.regplot(x='v_1',y = 'price',data = v_1_scatter_plot,scatter= True, fit_reg=True, ax=ax8)
v_14_scatter_plot = pd.concat([Y_train,Train_data['v_14']],axis = 1)
sns.regplot(x='v_14',y = 'price',data = v_14_scatter_plot,scatter= True, fit_reg=True, ax=ax9)
v_13_scatter_plot = pd.concat([Y_train,Train_data['v_13']],axis = 1)
sns.regplot(x='v_13',y = 'price',data = v_13_scatter_plot,scatter= True, fit_reg=True, ax=ax10)
结果如下: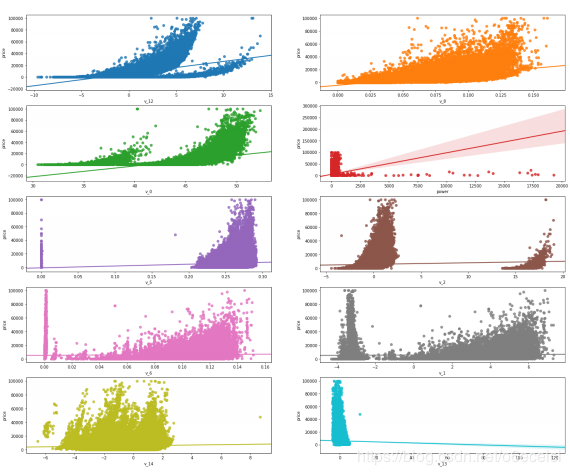
作者:o6eceici