Tensorflow实战入门:MNIST手写数字识别
本文是使用BP神经网络中的softmax回归模型实现MNIST手写数字识别,实际上能实现MNIST手写数字识别的神经网络还有CNN(卷积神经网络),下一篇可能会写。
Tensorflow是个什么东西Tensorflow是一个采用 数据流图,用于数值计算的开源软件库。节点在图中表示数学操作,图中的线则表示在节点间相互联系的多维数据数组,即张量(Tensor)。
数据流图用“结点”和“线”的有向图来描述数学计算。“节点” 一般用来表示施加的数学操作,但也可以表示数据输入的起点/输出的终点,或者是读取/写入持久变量的终点。“线”表示“节点”之间的输入/输出关系。这些数据“线”可以输运“size可动态调整”的多维数据数组,即“张量”。张量从图中流过的直观图像是这个工具取名为“Tensorflow”的原因,Tensor(张量)和Flow(流动)。
以上是从Tensorflow官网中摘录的一段文字,个人jio得介绍得挺贴切。把以上文字具象化理解,可以看下面这张图。

在Tensorflow中进行的所有计算,都可以用类似这样一种数据流图来表达。Tensorflow把计算定义在计算图中,把计算图送到会话中执行。Tensorflow把计算分为这么两步,目的是为了兼具开发效率和计算效率。
TensorFlow将计算过程完全运行在Python外部。
Tensorflow依赖于一个高效的C++后端来进行计算,并通过session连接。
先创建一个图,然后在session中启动它。
MNIST数据集编程语言入门有Hello World,机器学习入门有MNIST。
MNIST是一个入门级的计算机视觉数据集,它包含各种手写数字图片,它也包含每一张图片对应的标签,告诉我们这个是数字几。
MNIST数据集包含训练集(60000张)和测试集(10000张)
mnist.train mnist.train.images(60000,784) mnist.train.labels(6000,10) mnist.test mnist.test.images(10000,784) mnist.test.labels(10000,10) 用到的模型概述本次用到的神经网络模型简洁地用图来表示
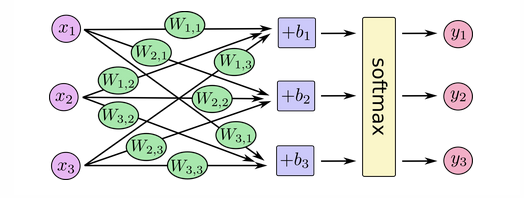
如图所示,本次用到的模型是BP神经网络中的softmax回归模型,模型中有一个输入层(接受特征输入)和一个输出层(输出层用了softmax激活函数)。
关于softmax函数的计算原理,可以看看这篇博客:一分钟理解softmax函数(超简单)
说白了softmax函数就是将一个样本分别属于各个类别的预测结果(暂且只是一系列的回归值,并没有转化为概率)输入softmax函数,进行非负性和归一化处理,最后得到0-1之内的分类概率。
开始撸代码代码逻辑分为两方面,分别是 定义计算图 和 执行会话
定义计算图
导入Tensorflowimport tensorflow as tf
MNIST数据集下载,可以先到Yann LeCun’s website官网把数据集下载下来

放在工程目录下的MNIST_data目录下
然后代码中使用tensorflow自带的一个库input_data把数据读取进来
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/",one_hot=True)
我们来看看这些图片长什么样
import matplotlib.pyplot as plt
img_bytes = mnist.train.images[2]
img = img_bytes.reshape([28, 28])*255
plt.imshow(img)
长这样,是一张手写的数字图片,像素为28 * 28
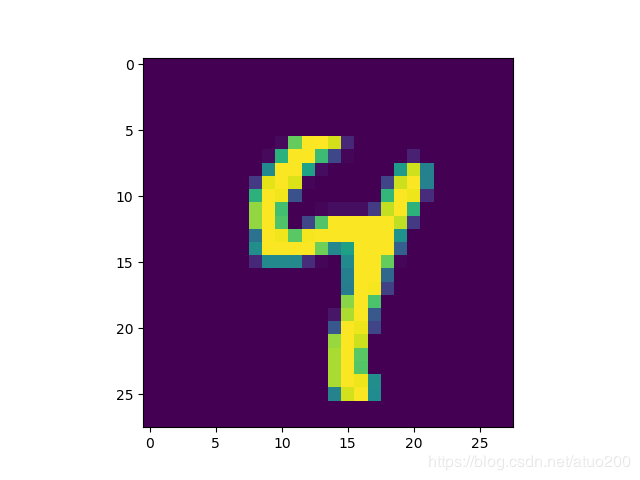
定义输入和输出的占位符,这里并不显式指定要输入的特征和特征对应的实际标签值
x_data = tf.placeholder(tf.float32, [None, 784]) # 占位符:输入
y_data = tf.placeholder(tf.float32, [None, 10]) # 占位符:输出
随机初始化神经网络的参数和阈值
w = tf.Variable(tf.zeros([784, 10])) # 参数矩阵
bias = tf.Variable(tf.zeros([10])) # 阈值
定义假设函数
y = tf.nn.softmax(tf.matmul(x_data, w) + bias) # 假设函数
定义损失函数
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_data*tf.log(y), axis=1)) # 损失函数(交叉熵)
选择优化器和定义训练节点
optimizer = tf.train.GradientDescentOptimizer(0.03) # 梯度下降法优化器
train = optimizer.minimize(cross_entropy) # 训练节点
评估模型在训练集上的精度
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_data,1))
这行代码会给我们一组布尔值。而为了确定正确预测项的比例,我们可以把布尔值转换成浮点数,然后 取平均值。例如,[True, False, True, True] 会变成 [1,0,1,1]
acc = tf.reduce_mean(tf.cast(correct_prediction, dtype=tf.float32)) #模型预测值与样本实际值比较的精度
执行会话
启动会话
sess = tf.Session()
会话执行变量初始化操作,当计算图中含有变量的时候一定要执行这一步
sess.run(tf.global_variables_initializer())
开始模型训练
for i in range(20000):
x_s, y_s = mnist.train.next_batch(100) #每次迭代批量地从数据集中获取数据
sess.run(train, feed_dict={x_data:x_s, y_data:y_s}) #模型训练
if i%1000 == 0: #每1000轮计算一次模型精度
acc_tr = sess.run(acc, feed_dict={x_data: x_s, y_data: y_s})
print(i, '轮训练的精度', acc_tr)
评估模型在测试集上的精度
acc_te = sess.run(acc, feed_dict={x_data:mnist.test.images, y_data:mnist.test.labels}) # 测试集精度
print('模型测试精度:', acc_te)
sess.close()
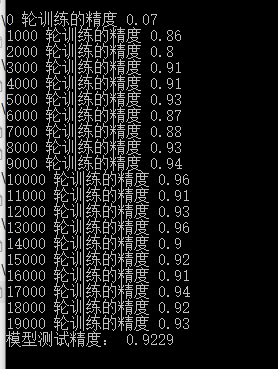
代码运行结果
最终的模型测试精度为0.9229,这个成绩还行,因为我们只是使用了一个比较简单的模型。
作者:阿坨