Pytorch自动求导函数详解流程以及与TensorFlow搭建网络的对比
在底层,每个原始的自动求导运算实际上是两个在Tensor上运行的函数。其中,forward函数计算从输入Tensor获得的输出Tensors。而backward函数接收输出,Tensors对于某个标量值得梯度,并且计算输入Tensors相对于该相同标量值得梯度。
在Pytorch中,可以容易地通过定义torch.autograd.Function的子类实现forward和backward函数,来定义自动求导函数。之后就可以使用这个新的自动梯度运算符了。我们可以通过构造一个实例并调用函数,传入包含输入数据的tensor调用它,这样来使用新的自动求导运算
以下例子,自定义一个自动求导函数展示ReLU的非线性,并调用它实现两层网络,如上一节
import torch
class myrelu(torch.autograd.Function):#自定义子类
# 通过建立torch.autograd的子类来实现自定义的autograd函数,并完成张量的正向和反向传播
@staticmethod
def forward(ctx, x):
# 在正向传播中,接受到一个上下文对象和一个包含输入的张量,必须返回一个包含输出的张量,可以使用上下文对象来缓存对象,以便在反向传播中使用
ctx.save_for_backward(x)
return x.clamp(min=0)
@staticmethod
def backward(ctx, grad_output):
"""
在反向传播中,我们接收到上下文对象和一个张量,
其包含了相对于正向传播过程中产生的输出的损失的梯度。
我们可以从上下文对象中检索缓存的数据,
并且必须计算并返回与正向传播的输入相关的损失的梯度。
"""
x, = ctx.saved_tensors
grad_x = grad_output.clone()
grad_x[x < 0] = 0
return grad_x
调用自定义的类实现两层网络
#%%
device=torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# n是批量大小,d_in是输入维度
# h是隐藏的维度,d_out是输出维度
n,d_in,h,d_out=64,1000,100,10
# 创建随机输入和输出数据,requires_grad默认设置为False,表示不需要后期微分操作
x=torch.randn(n,d_in,device=device)
y=torch.randn(n,d_out,device=device)
# 随机初始化权重,requires_grad默认设置为True,表示想要计算其微分
w1=torch.randn(d_in,h,device=device,requires_grad=True)
w2=torch.randn(h,d_out,device=device,requires_grad=True)
learning_rate=1e-6
for i in range(500):
#前向传播,使用tensor上的操作计算预测值y
#调用自定义的myrelu.apply函数
y_pred=myrelu.apply(x.mm(w1)).mm(w2)
#使用tensor中的操作计算损失值,loss.item()得到loss这个张量对应的数值
loss=(y_pred-y).pow(2).sum()
print(i,loss.item())
#使用autograd计算反向传播,这个调用将计算loss对所有的requires_grad=True的tensor梯度,
#调用之后,w1.grad和w2.grad将分别是loss对w1和w2的梯度张量
loss.backward()
#使用梯度下降更新权重,只想对w1和w2的值进行原地改变:不想更新构建计算图
#所以使用torch.no_grad()阻止pytorch更新构建计算图
with torch.no_grad():
w1-=learning_rate*w1.grad
w2-=learning_rate*w2.grad
#反向传播后手动将梯度置零
w1.grad.zero_()
w2.grad.zero_()
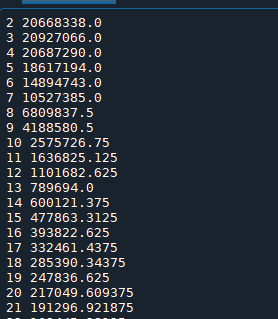
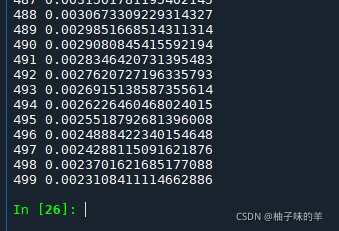
运行结果
…
PyTorch自动求导看似非常像TensorFlow:这两个框架中,都定义了计算图,使用自动微分来计算梯度,两者最大的不同是TensorFlow的计算图是静态的,而PyTorch使用的是动态的计算图。
在TensorFlow中,定义计算图一次,然后重复执行相同的图,可能会提供不同的输入数据,而在PyTorch中,每一个前向通道定义一个新的计算图。
**静态图的好处在于可以预先对图进行优化。**如:一个框架可以融合一些图的运算来提升效率,或者产生一个策略来将图分布到多个GPU或机器上。但是如果重复使用相同的图,那么重复运行同一个图时,前期潜在的代价高昂的预先优化的消耗就会被分摊。
静态图和动态图的一个区别就是控制流。对于一些模型,对每个数据点执行不同的计算。如:一个递归神经网络可能对于每个数据点执行不同的时间步数,这个展开可以作为一个循环来实现。对于一个静态图,循环结构要作为图的一部分。因此,TensorFlow提供了运算符将循环嵌入到图当中。对于动态图来说,情况更加简单:为每个例子即时创建图,使用普通的命令式控制流来为每个输入执行不同的计算。
使用TensorFlow拟合一个简单的两层网络(上面做对比):
#%%使用TensorFlow
import tensorflow.compat.v1 as tf #为了用placeholder不惜一切代价
tf.disable_v2_behavior()
import numpy as np
#%%
# 建立计算图
# n是批量大小,d_in是输入维度
# h是隐藏的维度,d_out是输出维度
n,d_in,h,d_out=64,1000,100,10
# 为输入和目标数据创建placeholder,在执行计算图时,他们将会被真实的数据填充
x=tf.placeholder(tf.float32,shape=(None,d_in))
y=tf.placeholder(tf.float32,shape=(None,d_out))
# 为权重创建variable并用随机数据初始化,TensorFlow的variable在执行计算图时不会改变
w1 = tf.Variable(tf.random_normal((d_in,h)))
w2=tf.Variable(tf.random_normal((h,d_out)))
# 前向传播:使用TensorFlow的张量运算计算预测值y(这段代码不执行任何数值运算,只是建立了稍后要执行的计算图)
h=tf.matmul(x,w1)
h_relu=tf.maximum(h,tf.zeros(1))
y_pred=tf.matmul(h_relu,w2)
# 使用TensorFlow的张量运算损失loss
loss=tf.reduce_sum((y-y_pred)**2.0)
# 计算loss对于权重w1和w2的导数
grad_w1,grad_w2=tf.gradients(loss,[w1,w2])
# 使用梯度下降更新权重,为了实际更新权重,我们需要在执行计算图时计算new_w1和new_w2
# 注:在TensorFlow中,更新权重值得行为是计算图的一部分,但在Pytorch中发生在计算图形之外
learning_rate=1e-6
new_w1=w1.assign(w1-learning_rate*grad_w1)
new_w2=w2.assign(w2-learning_rate*grad_w2)
# 现在搭建好了计算图,开始一个TensorFlow回话来执行计算图
with tf.Session() as sess:
# 运算一次计算图来出事话variable w1和w2
sess.run(tf.global_variables_initializer())
# 创建numpy数组存储输入x和目标y的实际数据
x_value=np.random.randn(n,d_in)
y_value=np.random.randn(n,d_out)
for i in range(500):
# 多次运行计算图,每次执行时,都有feed_dict参数,
# 将x_value绑定到x,将y_value绑定到y.每次执行计算图都要计算损失,
# new_w1和new_w2,这些张量的值以numpy数组的形式返回
loss_value,i,i=sess.run([loss,new_w1,new_w2],
feed_dict={x:x_value,y:y_value})
print(loss_value)
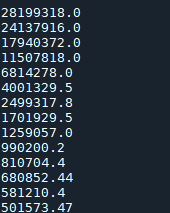
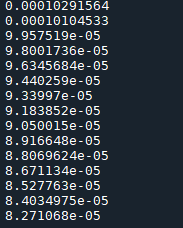
运行结果
…
今日告一段落,重点是比较了TensorFlow和Pytorch在自动求导中的区别——计算图前者是静态的,后者是动态的。
再见啦,明天可能不更~因为下午晚上都有课,虽然我可能不去上(哈哈哈哈哈哈哈哈,别学我)后面一节来写神经网络,不见不散!!
到此这篇关于Pytorch自动求导函数详解流程以及与TensorFlow搭建网络的对比的文章就介绍到这了,更多相关Pytorch 自动求导函数内容请搜索软件开发网以前的文章或继续浏览下面的相关文章希望大家以后多多支持软件开发网!