Python利用SVM算法实现识别手写数字
前言
使用 SVM 进行手写数字识别
参数 C 和 γ 对识别手写数字精确度的影响
完整代码
前言支持向量机 (Support Vector Machine, SVM) 是一种监督学习技术,它通过根据指定的类对训练数据进行最佳分离,从而在高维空间中构建一个或一组超平面。在博文《OpenCV-Python实战(13)——OpenCV与机器学习的碰撞》中,我们已经学习了如何在 OpenCV 中实现和训练 SVM 算法,同时通过简单的示例了解了如何使用 SVM 算法。在本文中,我们将学习如何使用 SVM 分类器执行手写数字识别,同时也将探索不同的参数对于模型性能的影响,以获取具有最佳性能的 SVM 分类器。
使用 SVM 进行手写数字识别我们已经在《利用 KNN 算法识别手写数字》中介绍了 MNIST 手写数字数据集,以及如何利用 KNN 算法识别手写数字。并通过对数字图像进行预处理( desew() 函数)并使用高级描述符( HOG 描述符)作为用于描述每个数字的特征向量来获得最佳分类准确率。因此,对于相同的内容不再赘述,接下来将直接使用在《利用 KNN 算法识别手写数字》中介绍预处理和 HOG 特征,利用 SVM 算法对数字图像进行分类。
首先加载数据,并将其划分为训练集和测试集:
# 加载数据
(train_dataset, train_labels), (test_dataset, test_labels) = keras.datasets.mnist.load_data()
SIZE_IMAGE = train_dataset.shape[1]
train_labels = np.array(train_labels, dtype=np.int32)
# 预处理函数
def deskew(img):
m = cv2.moments(img)
if abs(m['mu02']) < 1e-2:
return img.copy()
skew = m['mu11'] / m['mu02']
M = np.float32([[1, skew, -0.5 * SIZE_IMAGE * skew], [0, 1, 0]])
img = cv2.warpAffine(img, M, (SIZE_IMAGE, SIZE_IMAGE), flags=cv2.WARP_INVERSE_MAP | cv2.INTER_LINEAR)
return img
# HOG 高级描述符
def get_hog():
hog = cv2.HOGDescriptor((SIZE_IMAGE, SIZE_IMAGE), (8, 8), (4, 4), (8, 8), 9, 1, -1, 0, 0.2, 1, 64, True)
print("hog descriptor size: {}".format(hog.getDescriptorSize()))
return hog
# 数据打散
shuffle = np.random.permutation(len(train_dataset))
train_dataset, train_labels = train_dataset[shuffle], train_labels[shuffle]
hog = get_hog()
hog_descriptors = []
for img in train_dataset:
hog_descriptors.append(hog.compute(deskew(img)))
hog_descriptors = np.squeeze(hog_descriptors)
results = defaultdict(list)
# 数据划分
split_values = np.arange(0.1, 1, 0.1)
接下来,初始化 SVM,并进行训练:
# 模型初始化函数
def svm_init(C=12.5, gamma=0.50625):
model = cv2.ml.SVM_create()
model.setGamma(gamma)
model.setC(C)
model.setKernel(cv2.ml.SVM_RBF)
model.setType(cv2.ml.SVM_C_SVC)
model.setTermCriteria((cv2.TERM_CRITERIA_MAX_ITER, 100, 1e-6))
return model
# 模型训练函数
def svm_train(model, samples, responses):
model.train(samples, cv2.ml.ROW_SAMPLE, responses)
return model
# 模型预测函数
def svm_predict(model, samples):
return model.predict(samples)[1].ravel()
# 模型评估函数
def svm_evaluate(model, samples, labels):
predictions = svm_predict(model, samples)
acc = (labels == predictions).mean()
print('Percentage Accuracy: %.2f %%' % (acc * 100))
return acc *100
# 使用不同训练集、测试集划分方法进行训练和测试
for split_value in split_values:
partition = int(split_value * len(hog_descriptors))
hog_descriptors_train, hog_descriptors_test = np.split(hog_descriptors, [partition])
labels_train, labels_test = np.split(train_labels, [partition])
print('Training SVM model ...')
model = svm_init(C=12.5, gamma=0.50625)
svm_train(model, hog_descriptors_train, labels_train)
print('Evaluating model ... ')
acc = svm_evaluate(model, hog_descriptors_test, labels_test)
results['svm'].append(acc)

从上图所示,使用默认参数的 SVM 模型在使用 70% 的数字图像训练算法时准确率可以达到 98.60%,接下来我们通过修改 SVM 模型的参数 C 和 γ 来测试模型是否还有提升空间。
参数 C 和 γ 对识别手写数字精确度的影响SVM 模型在使用 RBF 核时,有两个重要参数——C 和 γ,上例中我们使用 C=12.5 和 γ=0.50625 作为参数值,C 和 γ 的设定依赖于特定的数据集。因此,必须使用某种方法进行参数搜索,本例中使用网格搜索合适的参数 C 和 γ。
for C in [1, 10, 100, 1000]:
for gamma in [0.1, 0.15, 0.25, 0.3, 0.35, 0.45, 0.5, 0.65]:
model = svm_init(C, gamma)
svm_train(model, hog_descriptors_train, labels_train)
acc = svm_evaluate(model, hog_descriptors_test, labels_test)
print(" {}".format("%.2f" % acc))
results[C].append(acc)
最后,可视化结果:
fig = plt.figure(figsize=(10, 6))
plt.suptitle("SVM handwritten digits recognition", fontsize=14, fontweight='bold')
ax = plt.subplot(1, 1, 1)
ax.set_xlim(0, 0.65)
dim = [0.1, 0.15, 0.25, 0.3, 0.35, 0.45, 0.5, 0.65]
for key in results:
ax.plot(dim, results[key], linestyle='--', marker='o', label=str(key))
plt.legend(loc='upper left', title="C")
plt.title('Accuracy of the SVM model varying both C and gamma')
plt.xlabel("gamma")
plt.ylabel("accuracy")
plt.show()
程序的运行结果如下所示:
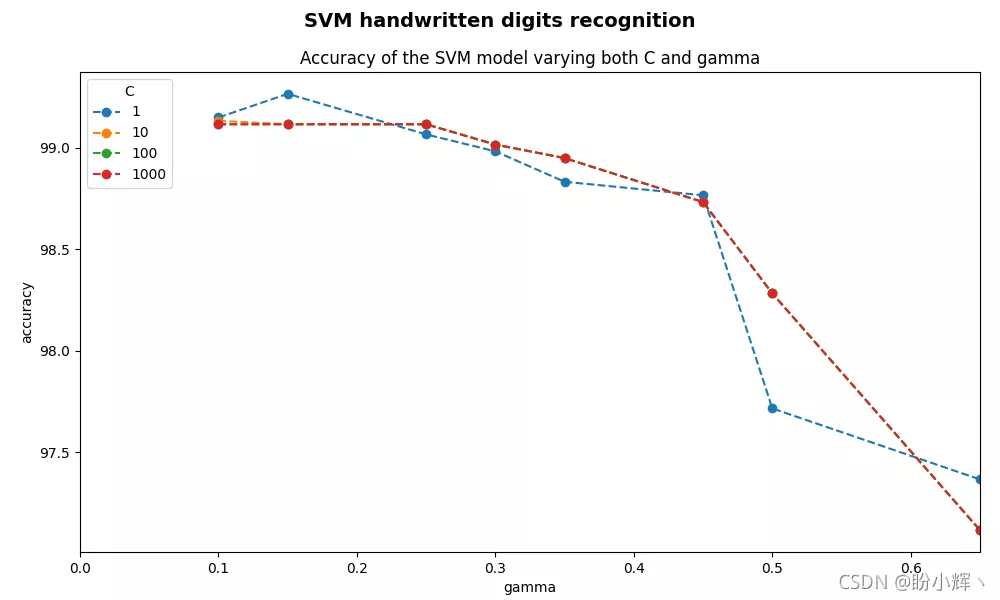
如图所示,通过使用不同参数,准确率可以达到 99.25% 左右。通过比较 KNN 分类器和 SVM 分类器在手写数字识别任务中的表现,我们可以得出在手写数字识别任务中 SVM 优于 KNN 分类器的结论。
完整代码程序的完整代码如下所示:
import cv2
import numpy as np
import matplotlib.pyplot as plt
from collections import defaultdict
import keras
(train_dataset, train_labels), (test_dataset, test_labels) = keras.datasets.mnist.load_data()
SIZE_IMAGE = train_dataset.shape[1]
train_labels = np.array(train_labels, dtype=np.int32)
def deskew(img):
m = cv2.moments(img)
if abs(m['mu02']) < 1e-2:
return img.copy()
skew = m['mu11'] / m['mu02']
M = np.float32([[1, skew, -0.5 * SIZE_IMAGE * skew], [0, 1, 0]])
img = cv2.warpAffine(img, M, (SIZE_IMAGE, SIZE_IMAGE), flags=cv2.WARP_INVERSE_MAP | cv2.INTER_LINEAR)
return img
def get_hog():
hog = cv2.HOGDescriptor((SIZE_IMAGE, SIZE_IMAGE), (8, 8), (4, 4), (8, 8), 9, 1, -1, 0, 0.2, 1, 64, True)
print("hog descriptor size: {}".format(hog.getDescriptorSize()))
return hog
def svm_init(C=12.5, gamma=0.50625):
model = cv2.ml.SVM_create()
model.setGamma(gamma)
model.setC(C)
model.setKernel(cv2.ml.SVM_RBF)
model.setType(cv2.ml.SVM_C_SVC)
model.setTermCriteria((cv2.TERM_CRITERIA_MAX_ITER, 100, 1e-6))
return model
def svm_train(model, samples, responses):
model.train(samples, cv2.ml.ROW_SAMPLE, responses)
return model
def svm_predict(model, samples):
return model.predict(samples)[1].ravel()
def svm_evaluate(model, samples, labels):
predictions = svm_predict(model, samples)
acc = (labels == predictions).mean()
return acc * 100
# 数据打散
shuffle = np.random.permutation(len(train_dataset))
train_dataset, train_labels = train_dataset[shuffle], train_labels[shuffle]
# 使用 HOG 描述符
hog = get_hog()
hog_descriptors = []
for img in train_dataset:
hog_descriptors.append(hog.compute(deskew(img)))
hog_descriptors = np.squeeze(hog_descriptors)
# 训练数据与测试数据划分
partition = int(0.9 * len(hog_descriptors))
hog_descriptors_train, hog_descriptors_test = np.split(hog_descriptors, [partition])
labels_train, labels_test = np.split(train_labels, [partition])
print('Training SVM model ...')
results = defaultdict(list)
for C in [1, 10, 100, 1000]:
for gamma in [0.1, 0.15, 0.25, 0.3, 0.35, 0.45, 0.5, 0.65]:
model = svm_init(C, gamma)
svm_train(model, hog_descriptors_train, labels_train)
acc = svm_evaluate(model, hog_descriptors_test, labels_test)
print(" {}".format("%.2f" % acc))
results[C].append(acc)
fig = plt.figure(figsize=(10, 6))
plt.suptitle("SVM handwritten digits recognition", fontsize=14, fontweight='bold')
ax = plt.subplot(1, 1, 1)
ax.set_xlim(0, 0.65)
dim = [0.1, 0.15, 0.25, 0.3, 0.35, 0.45, 0.5, 0.65]
for key in results:
ax.plot(dim, results[key], linestyle='--', marker='o', label=str(key))
plt.legend(loc='upper left', title="C")
plt.title('Accuracy of the SVM model varying both C and gamma')
plt.xlabel("gamma")
plt.ylabel("accuracy")
plt.show()
以上就是Python利用 SVM 算法实现识别手写数字的详细内容,更多关于Python SVM算法识别手写数字的资料请关注软件开发网其它相关文章!