[算法系列]搞懂DFS(2)——模式套路+经典例题详解（n皇后问题，素数环问题）

本文是算法系列递归讲解中讲述dfs的第二篇, 在上一篇: [算法系列]搞懂DFS(1)——经典例题(数独游戏, 部分和, 水洼数目)图文详解中, 已经通过三个例题讲述了dfs的思路以及设计方法, 本文先归纳常见dfs套路, 总结一般思路, 之后再通过两个经典例题(n皇后, 素数环) 进行巩固加深.

1. dfs常见模式

dfs本质上来说是对解空间所有解的一种枚举(遍历) , 但与暴力搜索所不同的是, 在进行求解时, 会优先考虑**“一条道走到黑, 不撞男墙不回头”(深度优先)** 进行遍历, 参考下面这幅图.

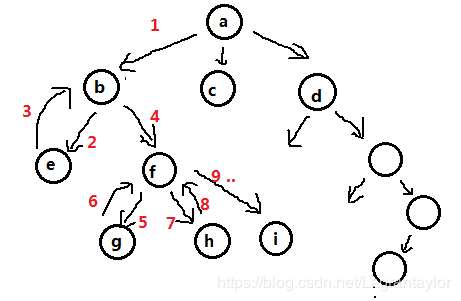
上图是一颗解答树, 你可以想成每一个结点都是我们在求解过程中的每一个 状态 ,比如在上篇的数独游戏中:

a 结点表示初始状态, b 结点表示在第一个位置选了一个数字(例如1)的状态, c结点表示在第一个位置选了另一个数字(例如2) e 结点表示在第一个位置上选了1之后, 再进一步于第二个位置选上一个数字(例如2)

从a -> b, b->e, g->f 这样在结点只见转移的我们称之为: 状态转移 其中,a->b相当于试探,e->b相当于回溯

现在我们来好好谈谈回溯:

回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

图中的e点就是一个走不下去的点,此时就只好回到b状态(如红色数字3),注意,此时这个位置理应也应当置为0,选上下一个选优条件,进行下一次试探.(在数独游戏中, 从1~9逐次选择数字就是一种选优条件,1不行咱选2,…)

道理就那么多,接下来看看dfs的思路:

定义状态: 通常状态就是我们所谓的函数及其参数, 每一个状态的区分关键在于参数内容不同 状态转移: 在于递归调用的过程,如上图的那些箭头 优选条件:按照怎样的一个规则去进行状态转移, 比如数独游戏中我们是从1~9由小到大逐个试探

那么再从递归问题的设计思路来看看dfs应该怎么解答:

找出口: 即通常所说的最小条件, 有时也是边界条件 找重复:对于当前问题的解法,应该是和子问题解法相同的,这一点不再赘述 找变化:在递归中有状态转移,往往就有变化的量(否则怎么能叫求解呢?)这一点通常将其作为参数

好了: 现在可以发挥想象力,大概写出dfs的伪代码:

dfs(参数1,参数2,参数3,...): if 边界条件: //副作用,比如添加到解集中 return 从候选集中按照选优条件取出一个 e: if e 符合条件: 这里可能改变状态,比如填上一个数字 dfs(参数1,参数2,参数3,...) //这里某些参数可能会变,以表示到达下一个状态,比如dfs(arr,x+1,y+1) 回溯,将刚刚的改变复位

这是大概模式,具体实现是要根据问题进行修改.下面来看看两道经典的题

2. n皇后问题 ''' n 皇后问题 在n×n格的棋盘上放置彼此不受攻击的n个皇后。 按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 即n后问题等价于再n×n的棋盘上放置n个皇后，任何2个皇后不妨在同一行或同一列或同一斜线上。 输入 n, 返回解法的个数 '''

如图为一个皇后的攻击范围:

如图为一个8皇后的解的状态:

任何两个皇后不在同一行同一列同一斜线上, 那么这样的解的状态有几种呢?

思路:

dfs呗,思路暴力而简单, 先在第一行放一个queue,再在下一排放下一个满足条件的q…以此类推,如果发现实在放不动了则回溯,寻找上一次的状态的下一个合法位置, 所有位置都不行则再次回溯…

状态确立很简单,即当前哪些位置上摆了queue, 现在需要考虑的是如何存储这一状态. 显然,二维数组是可以的,但是这有一个更为巧妙的存储方法: 用一个长度为n的一维数组rec,对应下标为对应行数,其相应值为放上queue的纵坐标位置. 例如:

rec[-100,-100,-100,-100,-100,-100,-100,-100,] 表示所有位置都没有queue rec[0,-100,-100,-100,-100,-100,-100,-100,] 表示第一行第一列行一个queue rec[0,6,3,5,7,1,4,2,] 表示即为上图这个合法结果

有了前面的基础,伪代码就不上了:

res = []#存放最终结果的list, 里面存放的每个正确结果的rec def n_queue(n): rec = [-100] *n #存放解, rec[i]表示第i行的皇后放在第rec[i]上 dfs_n_queue(rec,0) #从第0行开始 print(res) def dfs_n_queue(rec, row): if row == len(rec): # 如果达到边界,即所有行都移填上 rec_cp = rec.copy() res.append(rec_cp) #res中加入rec的克隆 return for y in range(0 , len(rec)): # 对当前行的每一列进行试探 if check(rec, row, y): # 判断每行每列每斜线,若没有第二个,则check返回true rec[row] = y # 检查成功,rec[row]=y 表示row+1行y+1列放入皇后 dfs_n_queue(rec, row + 1)#状态转移到下一个位置 rec[row ]= -100 # 均不合法,返回上一层前将该位置恢复 # 判断合法的函数 def check(rec , x, y): for i in range(0 , len(rec)): #判断同行 如果行数相同,跳过 if i == x : continue #判断同列: if rec[i] == y: return False #判断主对角线 比如 (0,0)和(1,1) =>横纵坐标差相等 if rec[i] - i == y-x: return False #判断副对角线 比如 (1,1)和(0,2) =>横纵坐标和相等 if rec[i] + i == y + x: return False return True n_queue(4) # print: [[1, 3, 0, 2], [2, 0, 3, 1]] 3. 素数环 ''' 输入正整数n,对1-n进行排列, 使得相 输出时从整数1开始,逆时针排列,同一个环应该恰好输出1次邻两个数之和均为质数 n<=16 如输入:6 输出: 1 4 3 2 5 6 1 6 5 2 3 4 '''

很显然也是可以用dfs进行求解的. 从第二个数开始, 对其左右两边进行求和(右边无数字则不求解)比如:

1,2 ... [满足] 1,2,3 ... [满足] 1,2,3 ... [满足] 1,2,3,4 ... [满足] 1,2,3,4,5 ... [不满足,回溯] 1,2,3,4,6,... [不满足,回溯] 1,2,3,4 ... [没有更多选择,继续回溯] 1,2,3, ... [没有更多选择,继续回溯] 1,2,5, ... ...

由上我们可以看到, 我们在求解过程中,实际上的思路的和暴力枚举有类似之处的.bingo, 其实从另一种角度来说, dfs的本质就是暴力枚举. 不过不同在于,我们一边列举,一边进行验证: 当发现1,2,3,4,5,已经不满足了,就没必要继续把6写上去,而进行回溯.

传统的暴力枚举是将所有串全部写出, 再来判断是否满足情况. 即该题中: 6位长度的串有6!中写法… 对空间要求过多.

也没有必要把整个串写完整再进行判断,比如1,2,3… 无论后面无论怎么填均不合法, 这可以直接pass了. 更为省时.

而将不满足的直接pass, 将整个解答树直接pass, 就是我们常常说的 剪枝 了. 当进入一个不可能为解的境地, 直接返回.

好了, 按照dfs模式和递归设计思路. 下面直接上代码

def zhishu_circle(n): rec = [0] * n #定义状态数组, 即上述的[1,2,3...] rec[0] = 1 dfs_zhishu_circle(n, rec, 1) # rec[0]固定为1,从下标为1开始 def dfs_zhishu_circle(n,rec,cur): if cur == n: #当前行到达边界,所有数字填完,得到结果 print(rec) return for tem in range(2 , n +1): #对2~n+1按顺序进行选择试探 if check_zhishu(n,rec,cur,tem): #如果满足题目要求 rec[cur] = tem dfs_zhishu_circle(n, rec ,cur+1) rec[cur] = 0 # 均不满足, 返回时恢复 def check_zhishu(n , rec, cur,tem): for i in range(0, cur): if rec[i] == tem : #这个数字当然取两遍 return False res_l = check_zhishu_core(rec[cur - 1] + tem) #判断左边和质数 if (rec[(cur+1) % n] == 0): #如果右边没填, 不考虑右边 res_r = True else: #否则也要考虑右边相邻和 res_r =check_zhishu_core(tem + rec[(cur + 1) % n]) return res_l and res_r import math #判断k是否为质数 def check_zhishu_core(k): for i in range(2, k): if (k % i == 0): return False return True

关于dfs 还有其他的介绍,比如图算法的一些内容, 树里面其他应用也是比较常见,不过在递归专题中,介绍到这里差不多啦.

如果对具体代码实现上(比如状态转移, 回溯)有一些问题的小伙伴可以倒回去看上一篇文章, 应该就能理解了.

接下来的文章将介绍 贪心, 动态规划等问题. 这两个和现在以及之前谈论话题的关系也极为紧密.

往期回顾:

[算法系列] 搞懂递归, 看这篇就够了 !! 递归设计思路 + 经典例题层层递进 [算法系列] 递归应用: 快速排序+归并排序算法及其核心思想与拓展 … 附赠 堆排序算法 [算法系列] 深入递归本质+经典例题解析——如何逐步生成, 以此类推,步步为营 [算法系列]搞懂DFS(1)——经典例题(数独游戏, 部分和, 水洼数目)图文详解
作者：Lawfree

n皇后 素数 素数环 dfs 算法