随机变量-离散-连续-假设检验方法
一组随机样本数据需要进行分析处理时,往往需要用到假设检验,对于离散变量discrete多用卡方检验,连续变量continuous用t检验或wilcoxon秩序和检验,具体的的使用场景如下
离散变量-卡方检验-适用条件四格表:
所有的理论数T≥5并且总样本量n≥40,用卡方进行检验 理论数T<5但T≥1并且n≥40,用连续性校正的卡方进行检验 有理论数T<1或n<40,用Fisher’s检验非四格表(R×C表):
R×C表中理论数小于5的格子不能超过1/5,且不能有小于1的理论数,用卡方进行检验 其他情况不能直接检验,要通过增加样本数、列合并等方法改变数据,再用合适的检验方法注:实际建模分析中,离散变量多是有多个因子水平的,所以大多是非四格表的形式,若不满足条件1:理论数小于5的格子不能超过1/5,通常都是把数据量小的组合并到相似或相近的组内,然后再进行检验分析
连续变量-T检验/wilcoxon秩序和检验-适用条件 非正态分布,用非参数方法wilcoxon秩序和检验 正态分布,用T检验,python中stats包中ttest_ind可区分是否是同方差离散变量代码示例:
class DiscreteTest():
def __init__(self):
pass
def _discrete_test(self, data, var, yname):
chisq_stat, chisq_p_val, df, expect = stats.chi2_contingency(pd.crosstab(data[yname], data[var]), correction=True)
# fourfold table
if expect.size == 4:
if (expect.sum() >= 40) and (expect.min()) >= 5:
stat, p_val, df, expect_show = stats.chi2_contingency(pd.crosstab(data[yname], data[var]), correction=True)
method = 'chisqtest'
elif (expect.sum() >= 40) and (expect.min() = 1):
stat, p_val, df, expect_show = stats.chi2_contingency(pd.crosstab(data[yname], data[var]), correction=False)
method = 'adj_chisqtest'
else:
prior_odds_ratio, p_val = stats.fisher_exact(pd.crosstab(data[yname], data[var]))
method = 'fisher'
# non-fourfold table
elif expect.size > 4:
if len(expect[expect < 5]) / expect.size <= 0.2:
stat, p_val, df, expect_show = stats.chi2_contingency(pd.crosstab(data[yname], data[var]), correction=False)
method = 'chisqtest'
else:
prior_odds_ratio, p_val = stats.fisher_exact(pd.crosstab(data[yname], data[var]))
method = 'fisher'
return {'p_value': p_val, 'method': method, 'var': var}
def _discrete_stat(self, data, discrete_vars, yname):
output = pd.DataFrame()
for var in discrete_vars:
temp = pd.DataFrame({"level": list(pd.Series(data[var]).value_counts().index),
'value': list(pd.Series(data[var]).value_counts().values)
})
temp['var'] = var
stat_t = self._discrete_test(data, var, yname)
temp['p_value'] = stat_t['p_value']
temp['method'] = stat_t['method']
output = output.append(temp, ignore_index=True)
return output
结果展示:
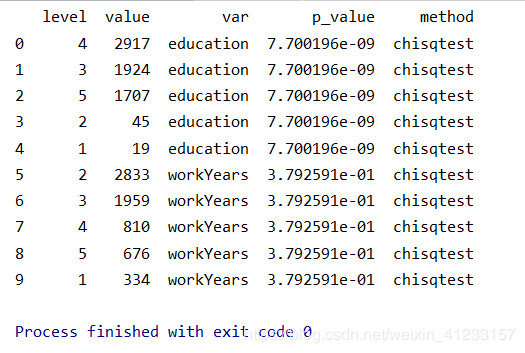
如图所知:
在α=5%的显著水平下,离散变量education和workYears运用卡方检验发现,education的p_valueα,不显著,接受原假设,workYears在正负样本间没有显著差异。
连续变量代码示例:
class ContinuousTest():
def __init__(self):
pass
def _continuous_test(self, data, var, yname):
# normal test
nor_stat = list()
nor_p_val = list()
for j in pd.unique(data[yname]):
nor_stat.append(stats.normaltest(data.loc[data[yname] == j, var])[0])
nor_p_val.append(stats.normaltest(data.loc[data[yname] == j, var])[1])
# homogeneity of variance test
f_stat, f_p_val = stats.f_oneway(data.loc[data[yname] == 0, var],data.loc[data[yname] == 1, var])
# T-test or wilcoxon rank-sum
if (min(nor_p_val) < 0.05):
# p<α,reject null hypothesis: x comes from a normal distribution,so use wilcoxon rank-sum statistic
stat, p_val = stats.ranksums(data.loc[data[yname] == 0, var], data.loc[data[yname] == 1, var])
method = "wilcoxon-ranksum"
elif f_p_val < 0.05:
# p0.05 and f_p_val variance is same
stat, p_val = stats.ttest_ind(data.loc[data[yname] == 0, var],data.loc[data[yname] == 1, var],equal_var=True)
method = "ttest, equal var"
stat_t = {'stat': stat, 'p_value': p_val, 'method': method, 'var': var}
return stat_t
def _continuous_stat(self, data, continuous_vars, yname):
output =pd.DataFrame()
for var in continuous_vars:
temp=pd.DataFrame({"level":list(pd.Series(data.loc[data[var].notnull(),var]).describe().index),
'value' :list(pd.Series(data.loc[data[var].notnull(),var]).describe().values)
})
temp['var'] = var
stat_t = self._continuous_test(data, var, yname)
temp['stat'] = stat_t['stat']
temp['p_value'] = stat_t['p_value']
temp['method'] = stat_t['method']
output = output.append(temp, ignore_index=True)
return output
结果展示:
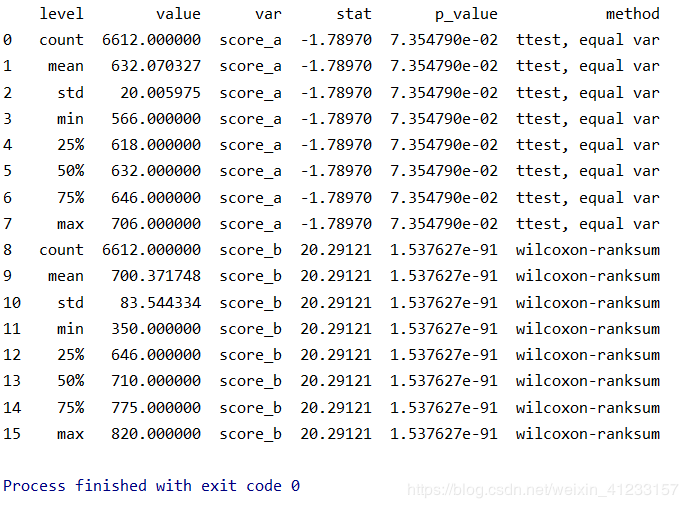
如图所知:
在α=5%的显著水平下,连续变量score_a运用T检验发现,p_value>α,不显著,不能拒绝原假设,所以score_a在正负样本间没有显著差异;同理,连续变量score_b运用wilcoxon-ranksum检验,p_value发现显著,拒绝原假设,score_b在正负样本间存在差异。
作者:will_vip
相关文章
Serwa
2020-03-20
Jenny
2020-05-14
Letitia
2020-11-28
Rae
2023-07-22
Rhoda
2023-07-22
Hester
2023-07-22
Grace
2023-07-22
Vanna
2023-07-22
Peony
2023-07-22
Dorothy
2023-07-22
Dulcea
2023-07-22
Zandra
2023-07-22
Serafina
2023-07-24
Kathy
2023-08-08
Olivia
2023-08-08
Elina
2023-08-08
Jacinthe
2023-08-08
Viridis
2023-08-08