【数论基础】欧几里德算法及其各种应用

Heidi ·

更新时间:2024-11-13

· 679 次阅读

目录：欧几里德算法（辗转相除法）1.问题引入：线段上格点的个数2.输入两个正整数，求最大公约数和最小公倍数3.P1029 最大公约数和最小公倍数问题 欧几里德算法（辗转相除法）

辗转相除法，又名欧几里德算法（Euclidean algorithm），是求最大公约数的一种方法。

1.问题引入：线段上格点的个数

问题描述：给定平面上的两个格点P1=(x1,y1)和P2=(x2,y2)，线段P1P2上，除P1和P2以外一共有几个格点？
限制条件：-109≤x1,y1,x2,y2≤109

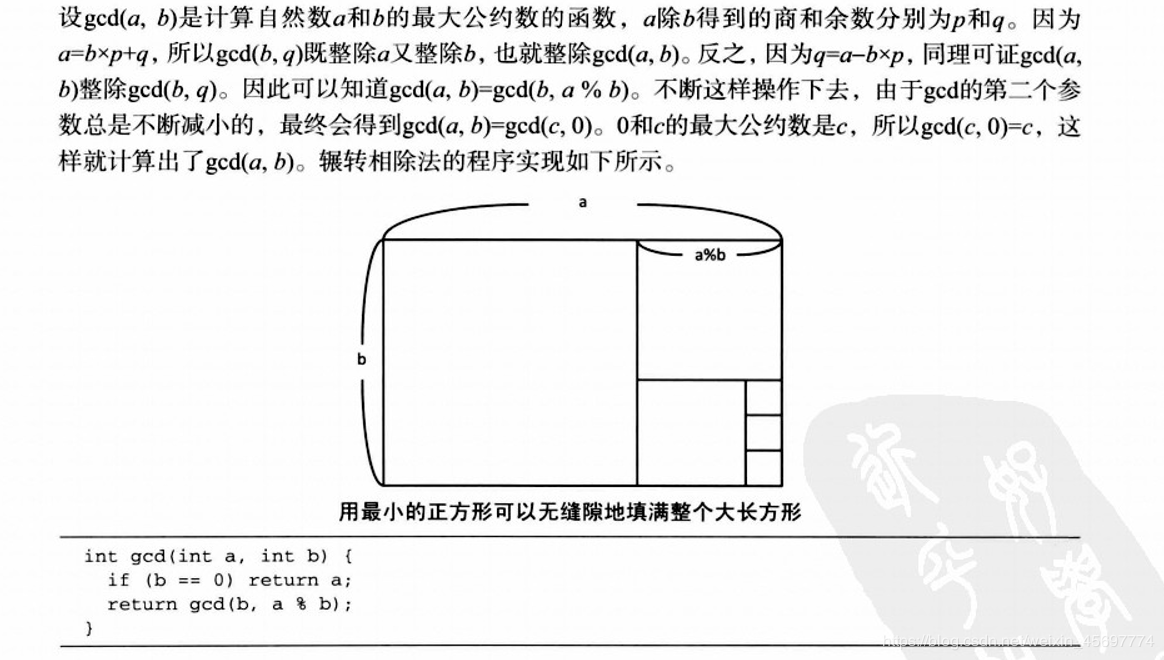
辗转相除法的原理：①a=b∗p+qa=b*p+qa=b∗p+q，所以gcd(b,q)gcd(b,q)gcd(b,q)既整除a又整除b，也就整除gcd(a,b)gcd(a,b)gcd(a,b)（公约数整除最大公约数）②q=a−b∗pq=a-b*pq=a−b∗p，同理可证gcd(a,b)gcd(a,b)gcd(a,b)整除gcd(b,q)gcd(b,q)gcd(b,q)。综上有gcd(a,b)=gcd(b,agcd(a,b)=gcd(b,a%b)gcd(a,b)=gcd(b,a。不断这样操作下去，由于gcd的第二个参数总是不断减小的，最后会出现gcd(a,b)=gcd(c,0)gcd(a,b)=gcd(c,0)gcd(a,b)=gcd(c,0)，而0和c的最大公约数就是c，所以gcd(c,0)=cgcd(c,0)=cgcd(c,0)=c，这样就计算出了gcd(a,b)gcd(a,b)gcd(a,b)

本题中虽然可以用穷举法，遍历min(x1,x2)≤x≤max(x1,x2)且min(y1,y2)≤y≤max(y1,y2)的格点可以得到正确答案，但是复杂度确实O(|x1−x2|×|y1−y2|)，其实这个题的答案是|x1−x2|和|y1−y2|的最大公约数减去1。（注意，|x1−x2|=0&&|y1−y2|=0时，答案为0）

原因
首先看一下|x1−x2|和|y1−y2|的
最大公约数代表的是啥？其实可以看成在横向和竖向的最大的公共等分数，比如 6 的等分点可以是 1:1:1:1:1:1分成6份 ,也可以是
2:2:2分成3份，或者是 6，只有1份。（其实对应的是 6能被6，3，1整除）那么 6和9的最大公共等分数是3，即6分为 2：2：2 ，
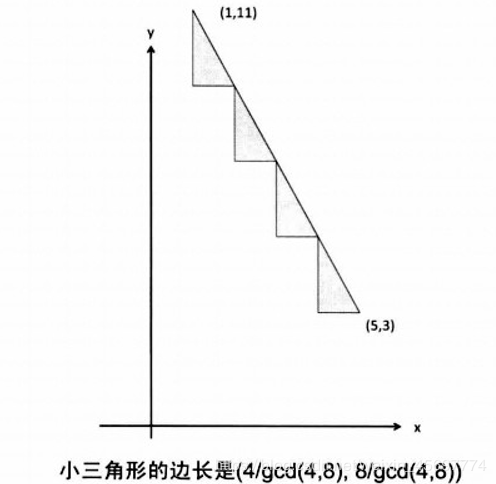
9分为3：3：3. 那么边长为6和9的矩形，按照这样分会是什么情况呢？

通过上图可以看出，大矩形的对角线正好经过 (2,3),(4,6),(6,9) 除开(6,9)，就是本体所要求的点。这就是为什么这个题的答案是|x1−x2|和|y1−y2|的最大公约数减去1。

那这个题可以转换为求最大公约数的问题，最大公约数一般使用辗转相除法

在这里插入图片描述

#include
using namespace std;
int gcd(int x, int y)
{
    if (y==0) return x;
    return gcd(y, x%y);
}
int x1,x2,y1,y2;
int main()
{
    cin>>x1>>y1>>x2>>y2;
    cout<<gcd(abs(x1-x2),abs(y1-y2))-1<<endl;
}

2.输入两个正整数，求最大公约数和最小公倍数

最大公约数和最小公倍数的乘积就是原两个数的积。

#include
using namespace std;
int gcd(int x, int y)
{
    if (y==0) return x;
    return gcd(y, x%y);
}
int m,n,d,e;
int main()
{
	scanf("%d%d",&m,&n);
	if(m < n)swap(n,m);
	printf("最大公约数=%d\n最小公倍数=%d\n",gcd(m,n),m*n/gcd(m,n));
	return 0;
 }

3.P1029 最大公约数和最小公倍数问题

在这里插入图片描述
要知道最大公约数和最小公倍数的乘积就是原两个数的积。
两种方法超详细解答链接