在Unity中实现Astar寻路算法
在游戏中,从一点到另一点的操作有时需要游戏系统自动完成,在一些带有rpg元素的游戏中,敌人在发现玩家位置后会自动向玩家的位置移动。这些移动的路线是如何自动确定的?本文将介绍寻路算法中的A*算法,并在unity中用C#脚本来实现寻路功能。
问题描述现在有两个点:起点A,和终点B,允许向周围的八个方向移动,如图所示。需要找到从起点A到终点B效率最高的路径。
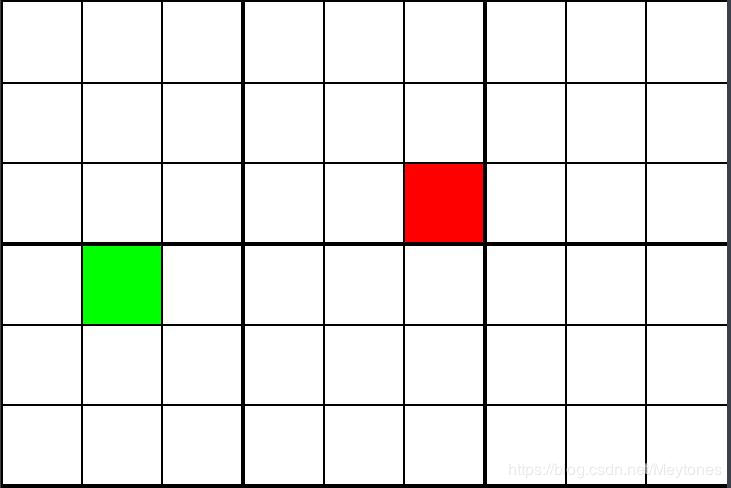
当不存在任何障碍物时,找到两点之间的最短路径似乎毫无难度:只需要每一步都选择离目标点最近的邻近点即可。
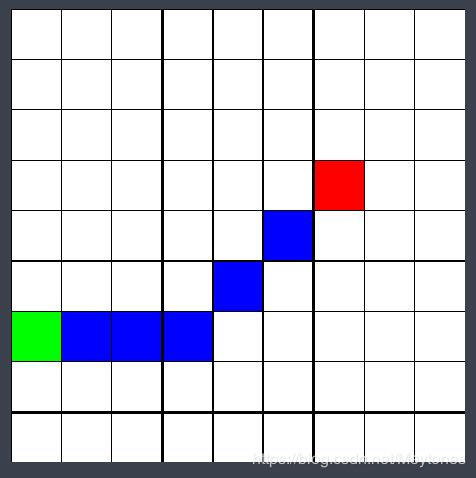
但是当存在障碍物时,路径上的点与目标点的距离并不是单调变化的,这时如何用一个普适性的思路来找出最优路径?
从数据结构的角度来看,网格化的地图是一种带有权值的无向图,而路径可以被视为由图中的结点组成的链表。因此,寻路的实质是在有权的图中,在所有以起点为头结点,终点为尾结点的链表中,选择长度最短的链表。
核心思想A*算法的核心思想是:使图中的每一个结点都处在使其权值最小的那条路径上。
权值的定义首先,需要确定权值,或者叫代价(cost)的计算方式。点在路径上的代价由两部分组成:从起点到该点的代价和从该点到终点的代价。
1.从起点到该点的代价
从起点起到该点的代价应当为每一步新增的代价的总和。每向正上、下、左、右方向走一步,代价增加10,每斜向走一步,代价增加14;
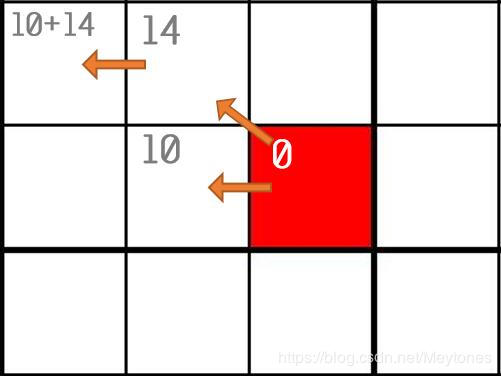
2.从该点到终点的代价
从该点到终点的代价是用来估量这个点到终点还需要的过程长短,可以用该点到目标点的直线距离*10来表示。
依照这个想法,由于每走一步只能移动至8邻域,所以每个点的前置结点必然是其8邻域中的一个。只要对其8邻域的每个点作为前置节点时的最小代价进行比较,选择代价最小的点作为前置结点,依此迭代至终点,再向上提取前置就可以得到最优路径。
那对如何确定所有点的搜索顺序呢?因为仍然需要优先考虑朝终点最近的点,所以依然以点的总代价作为搜索顺序的依据,总代价小的优先被搜索(因为代价最小的点意味着已经处于最优路径)。
总结以上讨论,可以整理出出一个思路:
设置一个待搜索结点的集合open。从起点开始,每搜索到一个点,就以其作为前置结点,计算其所有邻近点在该路径上的代价,并与邻近点已有的前置结点下的代价比较,如果当前点带来的代价更小,则更新前置结点,并使所有邻近点放入待搜索集合open。将该点移除集合open。再在open中选取代价最小的结点,重复以上操作,直至搜索到终点。
当第一次搜索到终点时,此时路径第一次被完成,即为最优路径。
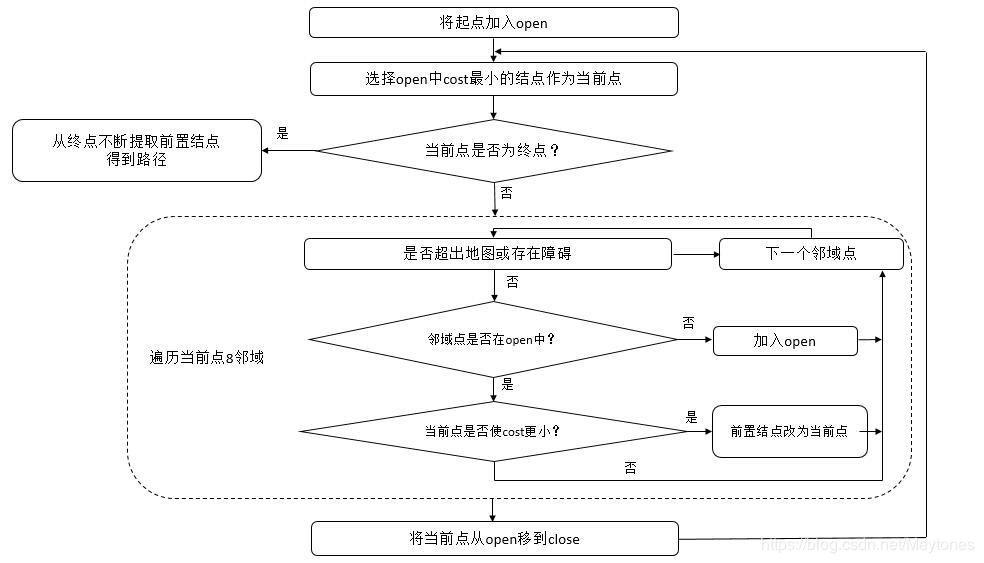
Unity中实现A*算法的代码如下所示。这里将路径和待搜索点集合都用List类来表示;编写结点类Node,存放位置、代价和前置结点,其中起点对应的结点前置节点为null。
//事先初始化的全局变量
Vector2 origin, destination;//起点和终点
int mapWidth, mapHeigth;//地图大小
bool[,] isBarrier;//判断是否为路障
List road;//路径存储
void Astar()
{
List open = new List();//待搜索的点
List close = new List();//已经搜索过一次或多次的点
Node current;
int minLocation;
float min;
//开始搜索
open.Add(new Node(origin, destination ,0));
do
{
//找出open中权值最小的结点移出open,加入close,并作为当前点
minLocation = 0;
min = open[0].cost;
for (int i = 0; i < open.ToArray().Length; i++)
{
minLocation = open[i].cost < min ? i : minLocation;
min = open[i].cost < min ? open[i].cost : min;
}
current = open[minLocation];
open.RemoveAt(minLocation);
close.Add(current);
//如果已经到达终点,路径搜索完成第一个,第一个构建的路径即为最优路径
if((current.position-destination).sqrMagnitude == 0){
break;
}
int index;//存储所有暂时需要保存的list中元素位置
//遍历当前点邻域,使所有点的前置节点都保证其代价更小
for (int i = -1; i <= 1; i++)
{
for (int j = -1; j = mapWidth || current.position.x + i = mapHeigth || current.position.y + j ((t.position - new Vector2(current.position.x + i, current.position.y + j)).sqrMagnitude == 0)))
{
continue;
}
//open中是否已经存在,如果不存在,添加进open,如果存在,看所在路径是否需要更新
Node temp = new Node(new Vector2(current.position.x + i, current.position.y + j), destination, current);
if (!open.Exists(t => ((t.position - new Vector2(current.position.x + i, current.position.y + j)).sqrMagnitude == 0)))
{
open.Add(temp);
}
else
{
index = open.FindIndex(t => ((t.position - new Vector2(current.position.x + i, current.position.y + j)).sqrMagnitude == 0));
//如果以current点为父节点计算出来的代价比现有代价小,改变其前置结点
if (open[index].cost > temp.cost)
{
open.RemoveAt(index);
open.Add(temp);
}
}
}
}
} while ((current.position - destination).sqrMagnitude != 0);
//将链中的结点提取出来
road.Add(current);
do
{
current = current.parent;
road.Add(current);
} while (current.parent != null);
}
//结点类
public class Node
{
public Vector2 position;
public float cost;//该点到目标点的预计代价
public float pre_cost;//从起点移动到该点的总代价
public float nex_cost;//从该点到终点的预计代价
public Node parent;//前置节点
//起点的结点(没有前置结点)
public Node(Vector2 location, Vector2 destination)
{
this.position = location;
cost = (destination - position).magnitude*10;
parent = null;
}
//带有父节点(前置节点)的Node
public Node(Vector2 location, Vector2 destination, Node parent)
{
this.position = location;
//斜向移动代价+14,正向移动代价+10
this.pre_cost = parent.pre_cost + (parent.position - location).sqrMagnitude > 1 ? 14 : 10;
nex_cost = (destination - position).magnitude * 10;
cost = pre_cost + nex_cost;
this.parent = parent;
}
}
最终效果
为了测试寻路算法的能力,利用Unity编写了一个以9*9的方格作为模拟地图的测试程序,实现了以下功能:
·重置地图并重新(随机)设置起点、终点(分别为红色和绿色);
·随机设置障碍;
·利用寻路算法寻路并显示(蓝色)。

看到在这些比较简单的条件下还是有非常不错的搜索效果的。
在寻路算法中,A*算法还只是静态条件下的基础算法,在具体的环境和需求下还需要对图中结点的代价的定义和更新有更复杂的要求。但不论是什么样的寻路,最终都是在所有的路径中寻找最优的代价分布。只要遵循这一思想,寻路的问题就都能找到突破的关键。
本博客的分享内容就到这里,如果我的分享能给您带来一点点帮助,那我会非常开心,因为那正是我分享的动力。非常感谢您的观看!
作者:RefmBiox