数值计算笔记之插值(四)三次样条插值
0、定义
已知函数
2、C++
程序我有用到矩阵库Armadillo,没有安装的请点这个安装教程链接
#include
#include
#include
using namespace std;
using namespace arma;
int main()
{
double x[] = { 0, 3, 5, 7, 9, 11, 12, 13, 14, 15 };
double y[] = { 0,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.0,1.6 };
int size = sizeof(x) / sizeof(double);
const double min = x[0];
const double max = x[size - 1];
vector xx, yy; //插值点与计算的函数值
for (double i = x[0]; i <= x[size - 1]; i = i + 0.1) {
xx.push_back(i);
}
int size_xx = xx.size();
vector dx, dy; //差分,即步长
for (int i = 0; i < size - 1; i++) {
double temp_dx = x[i + 1] - x[i];
dx.push_back(temp_dx);
double temp_dy = y[i + 1] - y[i];
dy.push_back(temp_dy);
}
mat H, Y, M; // H * M = Y
H.zeros(size, size);
Y.zeros(size,1);
//M.zeros(1, size);
H(0, 0) = 1;
H(size - 1, size - 1) = 1;
for (int i = 1; i < size - 1; i++) {
H(i, i - 1) = dx[i - 1];
H(i, i) = 2 * (dx[i - 1] + dx[i]);
H(i, i + 1) = dx[i];
Y(i) = 3 * (dy[i] / dx[i] - dy[i - 1] / dx[i - 1]);
}
M = solve(H,Y);
vector ai, bi, ci, di; //系数
for (int i = 0; i < size - 1; i++) {
ai.push_back(y[i]);
di.push_back((M(i + 1) - M(i)) / (3 * dx[i]));
bi.push_back(dy[i] / dx[i] - dx[i] * (2 * M(i) + M(i + 1)) / 3);
ci.push_back(M(i));
}
vector x_, xx_;
for (int i = 0; i < size; i++) {
int temp = x[i] / 0.1;
x_.push_back(temp);
}
for (int i = 0; i < size_xx; i++) {
int temp = xx[i] / 0.1;
xx_.push_back(temp);
}
for (int i = 0; i < size_xx; i++) {
int k = 0;
for (int j = 0; j = x_[j] && xx_[i] < x_[j + 1]) {
k = j;
break;
}
else if (xx[i] == x[size - 1]) {
k = size - 1;
}
}
//yy(i) = y[i] + bi(k) * (xx[i] - x[k]) + 1 / 2.0 * M(i) * pow((xx[i] - x[k]) , 2) + di(k) * pow((xx[i] - x[k]),3);
double temp = ai[k] + bi[k] * (xx[i] - x[k]) + M(k) * pow((xx[i] - x[k]), 2) + di[k] * pow((xx[i] - x[k]), 3);
yy.push_back(temp);
}
std::ofstream output;
output.open("Spline.txt");
for (unsigned i = 0; i < size_xx; i++) {
output << xx[i] << '\t' << yy[i] << std::endl;
}
output.close();
cout << "Hello World !" << endl;
}
结果用matlab显示为:

四、小结
1、算法流程
计算步长  根据边界条件填充矩阵
根据边界条件填充矩阵 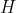 解矩阵方程
解矩阵方程  由
由 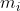 得到样条插值函数的系数
得到样条插值函数的系数




2、难点
三次样条插值的整体推导,以及 H 矩阵的填充。
作者:MinJinFan