数学建模之初等模型——商人过河问题(Matlab实现)
进入大学一年半了,发现许多不久前学过的知识转头就会忘并且自己的学习能力也没那么尽如人意,在知道了程序员的神器小黄鸭后,想着也许把我所学到的知识讲清楚分享出来更有利于自己的深度理解,同时也能帮到他人避开我所走的弯路。来到这个平台的目的就是分享自己的所学所感并与他人交流,大家共同进步。如果大家发现了我的问题(其实我挺菜的),请在评论区畅所欲言!
问题叙述三名商人和他们的三个仆从打算乘船过河。小船最多容纳两人,在河的任一岸,如果仆从的数量超过商人,仆从们就会杀人越货,如何才能让商人们安全过河呢?
构建模型首先把该问题抽象成一个简单的数学问题:我们将河左岸商人,仆从,和船所在的位置看作看作一个状态,并用一个向量(a,b,dir)加以描述:第一个分量代表左岸商人个数,第二个代表左岸仆从个数,第三个代表船所在的位置(-1为左岸,1为右岸)。接下来就是描述状态间的转移操作:我们用一个二维向量(p,q)代表船上商人和仆从的人数。那么从原状态(a,b,dir)经过操作(p,q)变为下一状态(c,d,new_dir)可以用该式表示:(c,d,new_dir)=(a,b,-dir)+dir*(p,q)。接下来我们的目标就是找到一个操作序列,使得初始状态(3,3,-1)在这个操作序列的作用下变为(0,0,1)。
模型求解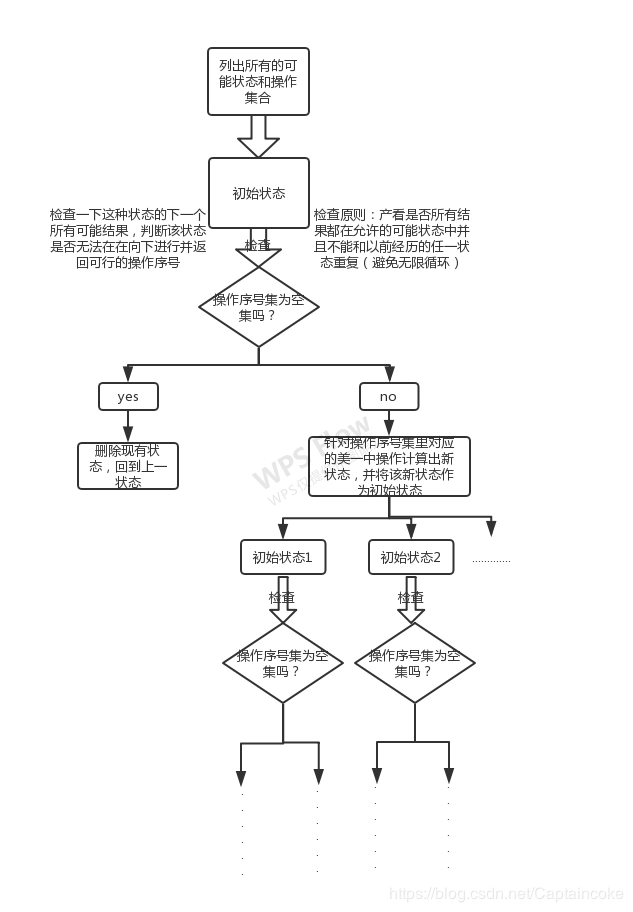
这里有的函数名后面会有个2,这个是为了和我之前的人狗鸡米问题(同样的解决思路)的函数区别一下,不必在意
function [ out ] = move_2( i )
%返回允许操作集的第i个操作
move=[1 0;0 1;2 0;1 1;0 2];
out=move(i,:);
end
function [ flag ] = check_status_2( status )
%检验是否在允许状态中,yes:1,no:0
status_permit=[3 3 1; 3 0 1;3 1 1;3 2 1;2 2 1;0 0 1;0 3 1;0 2 1;0 1 1;1 1 1] ;
temp=status_permit;
temp(:,end)=-temp(:,end);
status_permit=[status_permit;temp];
flag=0;
for i=1:size(status_permit,1)
if sum(status==status_permit(i,:))==3
flag=1;
end
end
end
function [ flag ] = check_same_2( status,pre_status )
%检查现有状态与之前状态是否有重复的,避免循环
m=size(pre_status,1);
flag=0;
for i=1:m
if sum(status==pre_status(i,:))==3
flag=1;
end
end
end
function [ flag,choice ] = checkallfail_2( pre_status )
%检验是否五种操作都不可行,并返回可行的操作序号
flag=0;sum=0;
laststatus=pre_status(end,:);
dir=laststatus(end);
choice=[];
for i=1:5
%对每一步的新状态进行检查
move=[move_2(i),0];
nextstatus=pre_status(end,:)+dir*move;
nextstatus(end)=nextstatus(end)*(-1);
p=abs(check_status_2(nextstatus)-1);
%检验下一状态是否在规定的允许状态集里面
q=check_same_2(nextstatus,pre_status);
%检查下一状态是否与已有的状态重复,避免无限循环
if p || q
sum=sum+1;
else
choice(end+1)=i;
end
end
if sum==5
flag=1;%若五种操作均不可以,那么判断该状态不可接受,回到上一状态
end
end
function [ newpre_status,newMove ] = allfail_2 (pre_status,Move )
%处理四种操作都不行的情况,删除现有状态,回到上一状态
pre_status(size(pre_status,1),:)=[];
newpre_status=pre_status;
Move(size(Move,1),:)=[];
newMove=Move;
end
function Print(status,move)
%输出方案
fprintf('初始---->操作---->结果\n');
for i=1:size(status,1)-1
st=status(i,:);
ed=status(i+1,:);
m=move(i,:);
fprintf('(%d,%d)-->(%d,%d)-->(%d,%d)\n',...
st(1),st(2),m(1),m(2),ed(1),ed(2));
end
function boat(status,move)
global ii;
[flag,choice]=checkallfail_2(status);
if flag==1
[status,move]=allfail(status,move);
end
temp_s=status;
temp_m=move;
for i=1:length(choice)
status=temp_s;
if sum(status(end,:)==[0 0 1])==3
ii=ii+1;
if mod(ii,2)==0
fprintf('方案(%d)\n',ii/2);
Print(status,move);
%不知道为什么最终会输出八种结果,不过奇数种和对应的偶数种是一样的,这里就只输出偶数种了
end
else
new_Status=operation(status(end,:),move_2(choice(i)));
new_Move=move_2(choice(i));
boat([status;new_Status],[move;new_Move]);
end
end
%主函数
Status(1,:)=[3 3 -1];
Move=[];
global ii;
ii=1;
boat(Status,Move);
结果
方案(1)
初始---->操作---->结果
(3,3)–>(1,1)–>(2,2)
(2,2)–>(1,0)–>(3,2)
(3,2)–>(0,2)–>(3,0)
(3,0)–>(0,1)–>(3,1)
(3,1)–>(2,0)–>(1,1)
(1,1)–>(1,1)–>(2,2)
(2,2)–>(2,0)–>(0,2)
(0,2)–>(0,1)–>(0,3)
(0,3)–>(0,2)–>(0,1)
(0,1)–>(1,0)–>(1,1)
(1,1)–>(1,1)–>(0,0)
方案(2)
初始---->操作---->结果
(3,3)–>(1,1)–>(2,2)
(2,2)–>(1,0)–>(3,2)
(3,2)–>(0,2)–>(3,0)
(3,0)–>(0,1)–>(3,1)
(3,1)–>(2,0)–>(1,1)
(1,1)–>(1,1)–>(2,2)
(2,2)–>(2,0)–>(0,2)
(0,2)–>(0,1)–>(0,3)
(0,3)–>(0,2)–>(0,1)
(0,1)–>(0,1)–>(0,2)
(0,2)–>(0,2)–>(0,0)
方案(3)
初始---->操作---->结果
(3,3)–>(0,2)–>(3,1)
(3,1)–>(0,1)–>(3,2)
(3,2)–>(0,2)–>(3,0)
(3,0)–>(0,1)–>(3,1)
(3,1)–>(2,0)–>(1,1)
(1,1)–>(1,1)–>(2,2)
(2,2)–>(2,0)–>(0,2)
(0,2)–>(0,1)–>(0,3)
(0,3)–>(0,2)–>(0,1)
(0,1)–>(1,0)–>(1,1)
(1,1)–>(1,1)–>(0,0)
方案(4)
初始---->操作---->结果
(3,3)–>(0,2)–>(3,1)
(3,1)–>(0,1)–>(3,2)
(3,2)–>(0,2)–>(3,0)
(3,0)–>(0,1)–>(3,1)
(3,1)–>(2,0)–>(1,1)
(1,1)–>(1,1)–>(2,2)
(2,2)–>(2,0)–>(0,2)
(0,2)–>(0,1)–>(0,3)
(0,3)–>(0,2)–>(0,1)
(0,1)–>(0,1)–>(0,2)
(0,2)–>(0,2)–>(0,0)
就是这样了,希望能帮到大家。代码水平和命名规范问题确实不容忽视,以后定加以改正
作者:Captaincoke