OI中常见的数学符号
整除/同余理论常见符号
1、整除符号
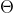 符号
符号
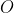 符号
符号
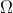 符号
符号
 符号
符号
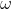 符号
符号




 努力的老周
努力的老周
 原创文章 289获赞 325访问量 110万+
关注
私信
展开阅读全文
原创文章 289获赞 325访问量 110万+
关注
私信
展开阅读全文
作者:努力的老周
。表示 x 整除 y,即 x 是 y 的因数。
。表示 x 除以 y 得到的余数。
。表示 x 和 y 互质。
gcd(x, y)。在无混淆意义的时候,可以写作 (x, y)。
5、最小公倍数lcm(x, y)。在无混淆意义的时候,可以写作 [x, y]。
数论常见符号 1、求和符号。表示满足特定条件的数的和。
。表示满足特定条件的数的积。
。
。特别规定:
。
。表示小于等于 x 的最大整数。
。表示大于等于 x 的最小整数。
一般用于复杂度表示。
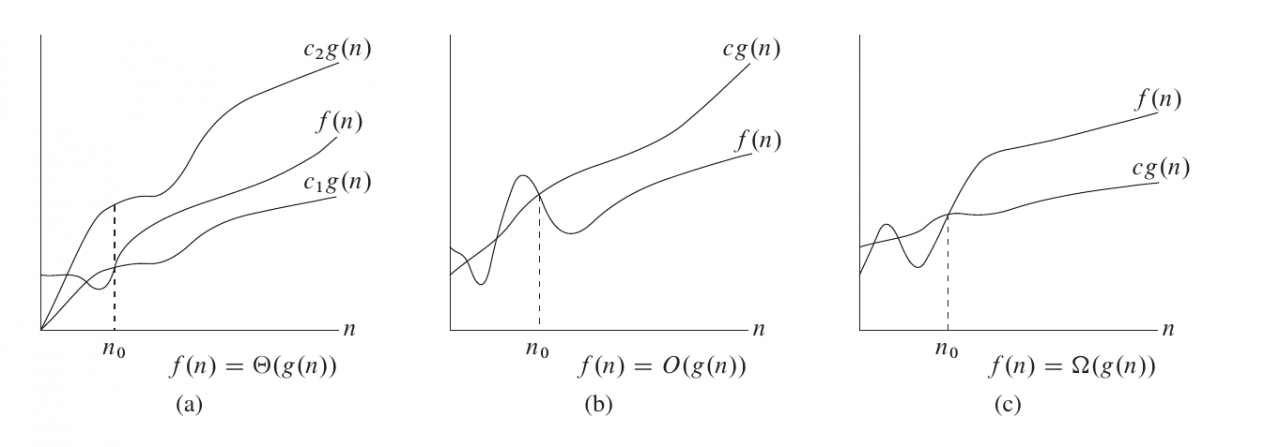
1、大对于给定的一个函数 g(n),,当且仅当
0" class="mathcode" src="https://private.codecogs.com/gif.latex?%5Cexists%20c_%7B1%7D%2C%20c_%7B2%7D%2C%20n_%7B0%7D%3E%200" />,使得
。
也就是说,如果函数 ,那么我们能找到两个正数
,使得 f(n) 被
和
夹在中间。
符号同时给了我们一个函数的上下界,如果我们只有一个函数的渐近上界的时候,我们使用
符号。
对于一个给定的函数 g(n),我们把它记作 。
,当切仅当
,使得
。
研究时间复杂度时,通常会使用 符号,因为我们关注通常是程序耗时的上界,而不关心其耗时的下界。
我们使用 符号来描述一个函数的渐近下届。
对于一个给定的函数 g(n),我们把它记作 。
,当切仅当
,使得
。
如果说大 符号相当于小于等于号,那么小
符号就相当于小于号。
如果说大 符号相当于小于等于号,那么小
符号就相当于小于号。
 努力的老周
努力的老周
 原创文章 289获赞 325访问量 110万+
关注
私信
展开阅读全文
原创文章 289获赞 325访问量 110万+
关注
私信
展开阅读全文
作者:努力的老周