P1379 八数码难题 题解
博客园同步
原题链接
简要题意:
给定一个 3×33 \times 33×3 的矩阵,每次可以把空格旁边(四方向)的一个位置移到空格上。求到目标状态的最小步数。
前置知识:
深度优先搜索(dfs\texttt{dfs}dfs).将这题作为 宽度优先搜索(bfs\texttt{bfs}bfs) 的模板题讲解!
首先,众所周知 dfs\texttt{dfs}dfs 的搜索树类似于这样:

其中,每个矩形都是一个状态,上面的数字是 时间戳(即搜索编号) ,红色的表示往下搜索,绿色的表示往上回溯。
dfs\texttt{dfs}dfs 大致分为 333 步:
从当前状态开始,依次搜索子状态,进入第 222 步。
如果当前状态 所有子状态都搜完了 或者 没有子状态,那么结束当前搜索,回溯至第 111 步。
找到答案即立刻一层层回溯结束;否则搜完所有状态返回无解。
你会发现,对于本题,如果你用 dfs\texttt{dfs}dfs,你不知道深度是多少,很有可能超时。(当然 记忆化 可以加快,但还是容易超时)因为 dfs\texttt{dfs}dfs 是 盲目搜索,直到当前状态搜完为止。那么,极有可能把所有状态都搜一遍。(即 9!=3628809! = 3628809!=362880)这是极其危险的!
下面引出一个概念:bfs\texttt{bfs}bfs.
求最小步数 / 最优解的情况下,bfs\texttt{bfs}bfs 一般比 dfs\texttt{dfs}dfs 要来的优。
先给出一个搜索状态图:
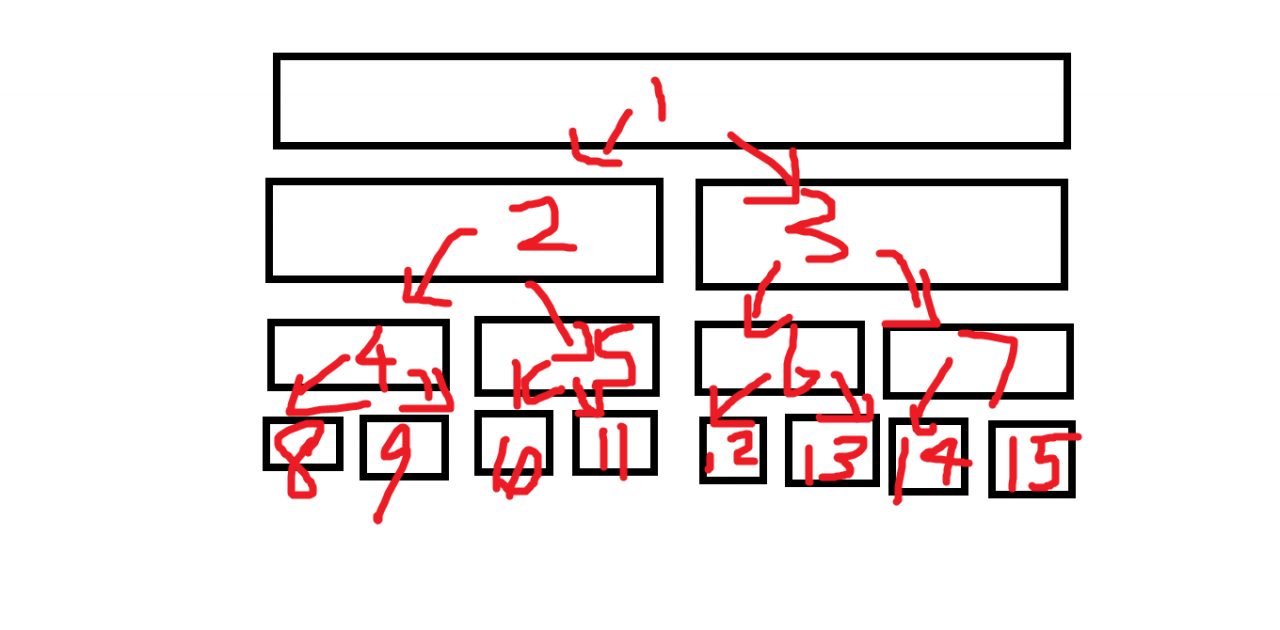
你会发现,bfs\texttt{bfs}bfs 的搜索是一层层搜的,即宽度优先的,并且没有任何回溯的过程。
而且,bfs\texttt{bfs}bfs 存在性质:
第一次到达的一定是最优的。(这是革命的本钱,没有它 bfs\texttt{bfs}bfs 就和 dfs\texttt{dfs}dfs 降为一样效率了)
一个状态保证只搜一次。(因为第一次是最优的,后面来的都是劣的,所以直接 开哈希剪枝。)
那么你会说:我们怎么实现呢?
用 queue\text{queue}queue 队列来实现,步骤如下:
将开始状态入队。
取出队首作为当前状态,把所有 当前状态能扩展出去的状态 都入队,并且做好哈希。然后 当前状态出队。
找到答案立刻停止搜索(因为性质 111 的存在可以这样做),否则搜完返回无解。
这样,先献出一段 bfs\texttt{bfs}bfs 的一般情况下的伪代码:
q.push(make_pair(x,y)); //x 是状态,y 是步数
h[x]=1; //哈希
while(!q.empty()) {
int t=q.front().x , step=q.front().y;
q.pop(); //取出队首,然后出队
for(/*枚举 t 能到达的状态 v*/)
if(!h[v]) {
h[v]=1; q.push(make_pair(v,step+1)); //哈希,入队
if(v == end) {printf("%d\n",step+1);return;} //搜到答案
}
} puts(/*无解情况*/); //搜完没有答案即无解
那么,比较两种搜索,你会发现:
如果 一定把所有情况搜完 ,那么 dfs\texttt{dfs}dfs 和 bfs\texttt{bfs}bfs 一样,都是遍历一遍。
如果 深度极深,但答案并不大,那么 bfs\texttt{bfs}bfs 的 宽度优先 策略会更优。
如果 深度、宽度相当 ,那么 dfs\texttt{dfs}dfs 和 bfs\texttt{bfs}bfs 效率一样,但 dfs\texttt{dfs}dfs 的代码相对简洁。(只是相对,因为一般新手会认为 dfs\texttt{dfs}dfs 更简单,不过写熟了都一样)
如果 深度极深,宽度极宽,那么两种搜索都不优时,我们就需要用 双向宽搜 或者 迭代加深搜索(即 IDA*\texttt{IDA*}IDA*) 再或者 A*\texttt{A*}A* 搜索 进行优化。(不过本题不用)
说了这么多,来研究这道题目。
状态:字符串,即矩阵。
答案:即记录步数。
哈希:用 map\text{map}map 实现字符串哈希。
队列:开结构体解决问题,写函数打包。
状态转移:将字符串的第 iii 位(这里 0≤i≤80 \leq i \leq 80≤i≤8)对应矩阵的 ⌊i3⌋\lfloor \frac{i}{3} \rfloor⌊3i⌋ 行,i%3i \% 3i%3 列,在矩阵上转移,然后再转回字符串。
时间复杂度:O(9!×9×log(9!))=O(3×105×9×18)=O(1.6×107)O(9! \times 9 \times \log (9!)) =O(3 \times 10^5 \times 9 \times 18) = O(1.6 \times 10^7)O(9!×9×log(9!))=O(3×105×9×18)=O(1.6×107),可以通过。
解释:9!9!9! 是遍历状态,999 是转移状态,log\loglog 是因为我们用了 map\text{map}map.(如果用 康托展开 进行优化哈希,那么可以达到 O(9!×9)=O(3.2×106)O(9! \times 9) = O(3.2 \times 10^6)O(9!×9)=O(3.2×106),会更优些)
实际得分:100pts100pts100pts.
时间:2.76s2.76s2.76s.(并不快,但是最慢的一个点是 257ms257ms257ms,可以接受)
空间:14.52MB14.52MB14.52MB.(并不大)
#pragma GCC optimize(2)
#include
using namespace std;
inline int read(){char ch=getchar();int f=1;while(ch'9') {if(ch=='-') f=-f; ch=getchar();}
int x=0;while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;}
struct node {
string s; int step;
};
//const int dx[4]={1,-1,3,-3};
const int dx[4]={0,0,1,-1};
const int dy[4]={-1,1,0,0}; //四方向矩阵转移
queue q;
map h;
string start,end="123804765";
inline node mp(string s,int step) {
node t; t.s=s; t.step=step;
return t;
} //结构体打包函数
inline int find(string s) {
for(int i=0;i<s.size();i++)
if(s[i]=='0') return i;
} //找到 0 的位置
inline void bfs() {
q.push(mp(start,0)); h[start]=1;
if(start==end) {puts("0");return;} //防止一开始就到终点
while(!q.empty()) {
string s=q.front().s;
int step=q.front().step;
// cout<<s<<" "<<step<<endl;
q.pop(); int wz=find(s); //找到 0 的位置
int x=wz/3,y=wz%3;
for(int i=0;i<4;i++) {
int nx=x+dx[i],ny=y+dy[i];
if(nx2 || ny2) continue;
swap(s[nx*3+ny],s[wz]); //交换
if(!h[s]) {
h[s]=1; q.push(mp(s,step+1));
if(s==end) {printf("%d\n",step+1);return;}
} swap(s[nx*3+ny],s[wz]); //记得换回去,不要影响后面的转移
}
}
}
int main(){
cin>>start;
bfs(); //搜索
return 0;
}
作者:bifanwen