数据压缩第二次作业-PCA入门
1.主成分分析:步骤、应用及代码实现。代码可以用任何你熟悉的编程语言。
2.藉由主成分分析这个问题,大家复习概率论与数理统计中的协方差矩阵等基本统计特征、特征值及特征向量等线性代数中的基本问题。
主成分分析,Principal Components Analysis,以下简称PCA,是一种将多指标信息简化处理的手段。
当我们处理的问题相对复杂,其含有的变量较多,之间相互依赖,存在很大的相关性。我们会想能否将其变量尽可能少的简化,且尽可能相互独立,而又不丢失问题的主要信息。
下面是一个许多资料讲述PCA时的入门例子
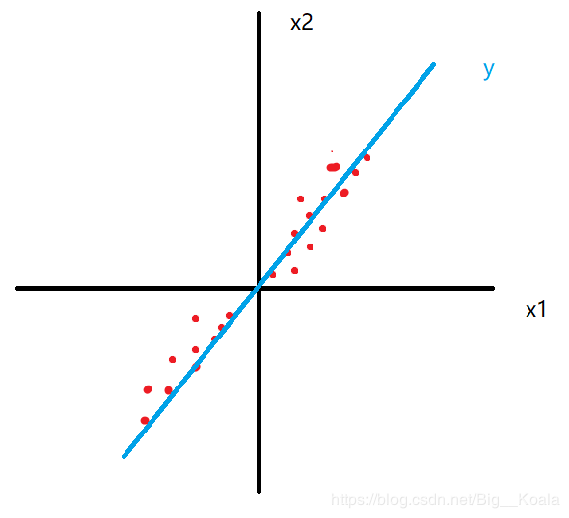
如图,在平面中分布着这些密密麻麻的红点,如果我们要用数学工具准确度量这些红点的位置,那么我们应当选定原点,建立二维坐标系,这样每个红点都可以相应的用其坐标(x1,x2)描述它的位置。
但是,如果细心观察,我们会发现,图中所示红点大都分布在直角坐标系的一三象限角平分线附近,它们的区别主要是沿着此角平分线到原点的距离不同,而在与其垂直的方向上距离大致相似,所以我们完全可以如图中蓝线一样建立一维坐标,用红点在蓝线的投影到原点的距离(y)作为红点的坐标。将本来需要两个变量的问题简化为一个变量。提取复杂问题的主要特征,忽略次要特征,从而将复杂问题简单化,这就是PCA的基本思想。
b2−4ac \sqrt {{b^2} - 4ac} \,b2−4ac
四、主成分分析的代码实现 1.在matlab中实现主成分分析在matlab中,可以很轻松的实现对数据的主成分分析,具体只需要掌握以下两个函数:
① R=corrcoef(X)
② [pc,latent,explained]=pcacov(R )
其中输入和输出的具体意义为
X是待处理的数据矩阵
R是X的相关系数矩阵
pc是由特征向量组成的矩阵
latent是特征值
explianed是因子贡献率
下面我们通过一道小的练习题目来熟悉并理解上述代码
为了研究杨树叶的形状,某小组测定了20片杨树叶的4个变量,变量名称和测量值如下,试求表示叶片长和宽的主分量。
| 叶长 | 2/3处宽 | 1/3处宽 | 1/2处宽 |
|---|---|---|---|
| 108 | 95 | 118 | 110 |
| 90 | 95 | 117 | 110 |
| 130 | 95 | 140 | 125 |
| 114 | 85 | 113 | 108 |
| 113 | 87 | 121 | 110 |
| 120 | 90 | 122 | 114 |
| 87 | 67 | 97 | 88 |
| 94 | 66 | 88 | 86 |
| 115 | 84 | 118 | 106 |
| 90 | 75 | 103 | 96 |
| 117 | 60 | 84 | 76 |
| 134 | 73 | 104 | 92 |
| 150 | 73 | 110 | 96 |
| 140 | 64 | 95 | 87 |
| 126 | 75 | 96 | 90 |
| 118 | 43 | 59 | 52 |
| 136 | 55 | 89 | 75 |
| 145 | 63 | 97 | 84 |
| 161 | 64 | 112 | 94 |
| 155 | 60 | 100 | 83 |
%将上述数据复制到excel中,命名为leaf.xlsx,和m文件保存在同意路径下
clear all;clc;close all;
xls=xlsread('leaf.xlsx');
R=corrcoef(xls);
[pc,latent,explained]=pcacov(R);
保存并运行,查看R,pc,latent,explained等输出值,结果如下
| R | |||
|---|---|---|---|
| 1 | -0.335455195390238 | 0.0143244496072770 | -0.173315089632803 |
| -0.335455195390238 | 1 | 0.886624018806103 | 0.957688254086229 |
| 0.0143244496072770 | 0.886624018806103 | 1 | 0.970714895509975 |
| -0.173315089632803 | 0.957688254086229 | 0.970714895509975 | 1 |
| pc | |||
|---|---|---|---|
| -0.148522129827538 | 0.954410942783761 | 0.251528033020049 | 0.0614375931427178 |
| 0.573489399716009 | -0.0984079145083256 | 0.773446323537859 | -0.251409179190543 |
| 0.557678101719958 | 0.269500419135760 | -0.558548657150497 | -0.551713745109771 |
| 0.581417423394661 | 0.0823720750156525 | -0.162904360918333 | 0.792862403084241 |
| latent | |||
|---|---|---|---|
| 2.91998310252916 | 1.02367488341228 | 0.0489183138262180 | 0.00742370023234820 |
| explained | |||
|---|---|---|---|
| 72.9995775632289 | 25.5918720853070 | 1.22295784565545 | 0.185592505808705 |
作者:Big__Koala