Iris数据集的 Fisher线性分类以及数据可视化

Faustine ·

更新时间:2024-11-01

· 989 次阅读

这用Jupyter完成Iris数据集的 Fisher线性分类，并学习数据可视化技术。里写目录标题用Jupyter完成Iris数据集的 Fisher线性分类，并学习数据可视化技术。一、完成Iris数据集的 Fisher线性分类判断准确率二、学习数据可视化1、数据概览1.1、读取文件1.2、前五行数据1.3、后五行数据1.4、查看数据整体信息1.5、描述性统计1.6、对每种特征计数2、特征工程2.1、引入可视化所需要的库2.2、去掉Species下的字符2.2、绘制花萼的长度与宽度的散点图2.3、绘制花瓣的长度与宽度的散点图2.4、Id编号与花萼长度, 花萼宽度, 花瓣长度, 花瓣宽度之间的关系2.5、散点图与直方图的同时显示2.6、绘制直方图2.7、绘制箱线图2.8、绘制琴图2.9、绘制分布图 用Jupyter完成Iris数据集的 Fisher线性分类，并学习数据可视化技术。 一、完成Iris数据集的 Fisher线性分类判断准确率

python代码如下所示：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt 
path=r'media/Iris.csv'
df = pd.read_csv(path, header=0)
Iris1=df.values[0:50,0:4]
Iris2=df.values[50:100,0:4]
Iris3=df.values[100:150,0:4]
m1=np.mean(Iris1,axis=0)
m2=np.mean(Iris2,axis=0)
m3=np.mean(Iris3,axis=0)
s1=np.zeros((4,4))
s2=np.zeros((4,4))
s3=np.zeros((4,4))
for i in range(0,30,1):
    a=Iris1[i,:]-m1
    a=np.array([a])
    b=a.T
    s1=s1+np.dot(b,a)    
for i in range(0,30,1):
    c=Iris2[i,:]-m2
    c=np.array([c])
    d=c.T
    s2=s2+np.dot(d,c) 
    #s2=s2+np.dot((Iris2[i,:]-m2).T,(Iris2[i,:]-m2))
for i in range(0,30,1):
    a=Iris3[i,:]-m3
    a=np.array([a])
    b=a.T
    s3=s3+np.dot(b,a) 
sw12=s1+s2
sw13=s1+s3
sw23=s2+s3
#投影方向
a=np.array([m1-m2])
sw12=np.array(sw12,dtype='float')
sw13=np.array(sw13,dtype='float')
sw23=np.array(sw23,dtype='float')
#判别函数以及T
#需要先将m1-m2转化成矩阵才能进行求其转置矩阵
a=m1-m2
a=np.array([a])
a=a.T
b=m1-m3
b=np.array([b])
b=b.T
c=m2-m3
c=np.array([c])
c=c.T
w12=(np.dot(np.linalg.inv(sw12),a)).T
w13=(np.dot(np.linalg.inv(sw13),b)).T
w23=(np.dot(np.linalg.inv(sw23),c)).T
#print(m1+m2) #1x4维度  invsw12 4x4维度  m1-m2 4x1维度
T12=-0.5*(np.dot(np.dot((m1+m2),np.linalg.inv(sw12)),a))
T13=-0.5*(np.dot(np.dot((m1+m3),np.linalg.inv(sw13)),b))
T23=-0.5*(np.dot(np.dot((m2+m3),np.linalg.inv(sw23)),c))
kind1=0
kind2=0
kind3=0
newiris1=[]
newiris2=[]
newiris3=[]
for i in range(30,49):
    x=Iris1[i,:]
    x=np.array([x])
    g12=np.dot(w12,x.T)+T12
    g13=np.dot(w13,x.T)+T13
    g23=np.dot(w23,x.T)+T23
    if g12>0 and g13>0:
        newiris1.extend(x)
        kind1=kind1+1
    elif g120:
        newiris2.extend(x)
    elif g13<0 and g230 and g13>0:
        newiris1.extend(x)
    elif g120:
        newiris2.extend(x)
        kind2=kind2+1
    elif g13<0 and g230 and g13>0:
        newiris1.extend(x)
    elif g120:     
        newiris2.extend(x)
    elif g13<0 and g23<0 :
        newiris3.extend(x)
        kind3=kind3+1
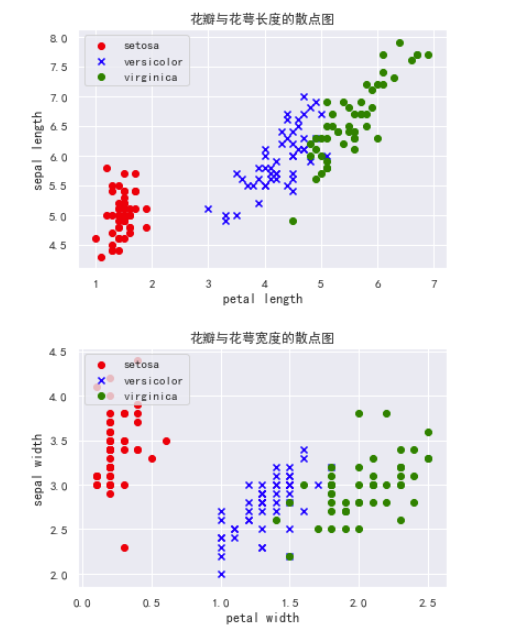
#花瓣与花萼的长度散点图
plt.scatter(df.values[:50, 3], df.values[:50, 1], color='red', marker='o', label='setosa')
plt.scatter(df.values[50:100, 3], df.values[50: 100, 1], color='blue', marker='x', label='versicolor')
plt.scatter(df.values[100:150, 3], df.values[100: 150, 1], color='green', label='virginica')
plt.xlabel('petal length')
plt.ylabel('sepal length')
plt.title("花瓣与花萼长度的散点图")
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False
plt.legend(loc='upper left')
plt.show()
#花瓣与花萼的宽度度散点图
plt.scatter(df.values[:50, 4], df.values[:50, 2], color='red', marker='o', label='setosa')
plt.scatter(df.values[50:100, 4], df.values[50: 100, 2], color='blue', marker='x', label='versicolor')
plt.scatter(df.values[100:150, 4], df.values[100: 150, 2], color='green', label='virginica')
plt.xlabel('petal width')
plt.ylabel('sepal width')
plt.title("花瓣与花萼宽度的散点图")
plt.legend(loc='upper left')
plt.show()
correct=(kind1+kind2+kind3)/60
print("样本类内离散度矩阵S1：",s1,'\n')
print("样本类内离散度矩阵S2：",s2,'\n')
print("样本类内离散度矩阵S3：",s3,'\n')
print('-----------------------------------------------------------------------------------------------')
print("总体类内离散度矩阵Sw12：",sw12,'\n')
print("总体类内离散度矩阵Sw13：",sw13,'\n')
print("总体类内离散度矩阵Sw23：",sw23,'\n')
print('-----------------------------------------------------------------------------------------------')
print('判断出来的综合正确率：',correct*100,'%')

运行结果

原创文章 10获赞 9访问量 1353 关注私信展开阅读全文
作者：missbearC