数据结构之稀疏矩阵的三元组顺序表储存以及转置

Valencia ·

更新时间:2024-11-13

· 805 次阅读

今天学习了矩阵的压缩存储，主要是特殊矩阵和稀疏矩阵的压缩储存，特殊矩阵包括对称、对角、上下三角矩阵，实现起来比较方便，这里我主要实现了一遍稀疏矩阵的三元组顺序表存储实现以及两种矩阵转置方法。

稀疏矩阵

稀疏矩阵一直没有一个明确的定义，大概的解释就是矩阵中的非零元分布不是规律的，矩阵中非零元的个数占整个矩阵元个数的比例，该比例成为稀疏因子，只要稀疏因子小于等于0.05，则该矩阵就可叫做稀疏矩阵

三元组顺序表

因为稀疏矩阵中的矩阵元分布不是规律的，所以一个非零元的表示需要行列坐标和本身数据表示，包含三个元素：非零元的行、列以及数据，所以叫做三元组。而矩阵还需要包含总的行数、列数，以及总的非零元个数，对应的代码表示为：

//非零元三元组
typedef struct matrixNode {
	int i, j;   //这里没改名称，i代表行、j代表列
	int Elemdata;  //数据
}matNode;
//稀疏矩阵表示
typedef struct Matrix {
	int mu, nu, tu;   //mu代表总的行数、nu代表总的列数、tu代表总的非零元个数
	matNode data[MAX_NUM];
}matrix;

矩阵压缩存储

//矩阵的压缩储存
matrix matrixStorage(int  array[][3],int row,matrix Matrix) {
	int count = 0;
	int index = 0;
	//遍历矩阵
	for (int a = 0; a < row; ++a) {
		for (int b = 0; b < sizeof(array[0]) / sizeof(array[0][0]); ++b) {
		//非零则存储，否则不存储
			if (array[a][b]) {
				Matrix.data[index].Elemdata = array[a][b];
				Matrix.data[index].i = a;
				Matrix.data[index].j = b;
				count++;
				index++;
			}
		}
	}
	Matrix.mu = row;  //行数
	Matrix.nu = sizeof(array[0]) / sizeof(array[0][0]); //列数
	Matrix.tu = count; //非零元个数
	return Matrix;
}

这一步是将矩阵进行压缩：非零元分配一个储存空间，零元素不分配（这里未实现相同元素只占一个空间，后面有空实现），这里看代码应该看到懂

转置 第一种转置

/矩阵转置
matrix matrixTranspose(matrix Iintmatrix, matrix Aftermatrix) {
//转置后的行列互换
	Aftermatrix.mu = Iintmatrix.nu;
	Aftermatrix.nu = Iintmatrix.mu;
	Aftermatrix.tu = Iintmatrix.tu;
	int q = 0;
	for (int col = 0; col < Iintmatrix.nu; ++col) {
		for (int p = 0; p < Iintmatrix.tu; ++p) {
			if (Iintmatrix.data[p].j == col) {//用待转置矩阵非零元的列位置匹配当前列
			//进行三元表位置的改变
				Aftermatrix.data[q].i = Iintmatrix.data[p].j;
				Aftermatrix.data[q].j = Iintmatrix.data[p].i;
				Aftermatrix.data[q].Elemdata = Iintmatrix.data[p].Elemdata;
				q++;
			}
		}
	}
	return Aftermatrix;
}

矩阵转置的要点就是交换矩阵前后的行列数以及数据的行列位置，该种方法是按照转置后的三元组的次序去转置前的对应三元组次序寻找，也就是按照转置前的列序来转置

快速矩阵转置

//快速矩阵转置
matrix  fastMatrixTranspose(matrix InitMatrix,matrix Aftermatrix) {
	int num[MAX_NUM];
	int copt[MAX_NUM];
	Aftermatrix.mu = InitMatrix.nu;
	Aftermatrix.nu = InitMatrix.mu;
	Aftermatrix.tu = InitMatrix.tu;
	for (int col = 0; col < InitMatrix.nu; col++)
		num[col] = 0;  //初始化num
	for(int t = 0;t < InitMatrix.tu;++t) 
		++num[InitMatrix.data[t].j]; //计算每列的非零元个数
	 copt[0] = 0;
    for (int col = 1; col < InitMatrix.nu; col++) 
		 copt[col] = copt[col - 1] + num[col - 1];  //计算每列第一个非零元在转之后的位置
	for (int t = 0; t < InitMatrix.tu; ++t) {
		 int col = InitMatrix.data[t].j; 
		 int q = copt[col];
		 Aftermatrix.data[q].i = InitMatrix.data[t].j;
		 Aftermatrix.data[q].j = InitMatrix.data[t].i;
		 Aftermatrix.data[q].Elemdata = InitMatrix.data[t].Elemdata;
		 ++copt[col];
	 }
	 return Aftermatrix;
}

这个转置方法附设了两个向量：代表每列非零元个数总数的数组num[];和代表每列第一个非零元在转置后的三元组的位置

结果

int main() {  
	int array[][3] = { { 0,1,0},{2, 0, 0}, {0, 1, 3}};
	matrix m1;
	matrix m2;
	m1.mu = 0;
	m1.nu = 0;
	m1.tu = 0;
	m2.mu = 0;
	m2.nu = 0;
	m2.tu = 0;
	int row = 0;
	row = sizeof(array) / sizeof(array[0]);
	m1 = matrixStorage(array,row,m1);
//	m2 = matrixTranspose(m1,m2);
	m2 = fastMatrixTranspose(m1,m2);
	//Print
	cout << "before：" << endl;
	for (int i = 0; i < m1.tu; ++i)
		cout << m1.data[i].Elemdata << " ";
	cout << endl;
	cout << "After：" << endl;
	for (int i = 0; i < m2.tu; ++i)
		cout << m2.data[i].Elemdata << " ";
	cout << endl;
	system("pause");
	return EXIT_SUCCESS;
}

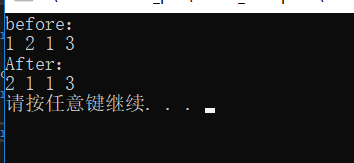
在这里插入图片描述

总结

对比上面两种转置可以看出：
第一种转置的时间复杂度是O(nuxtu);当tu的数量级达到mu x nu数量级时间，时间复杂度达到了O（mu x nu x nu），所以说该方法适合tu<<mu x nu的情况。
第二种方法是四个循环，对应的时间复杂度是O（nu+tu）;当tu的数量级达到mu x nu的时候，时间复杂度是O（mu xnu），相对于第一种降低不少，所以叫做快速算法