数据结构与算法Python版第九周OJ作业
题目内容:
给定一种序列化二叉树的方式:从根节点起始按层次遍历二叉树所有“可能”存在节点的位置:若该位置存在节点,则输出节点值,并在下一层相应增加两个可用位置;否则输出None,且不增加下一层的可用位置。
例如"[5, 4, 7, 3, None, 2, None, -1, None, 9]"是下图所示的二叉树序列化的结果:
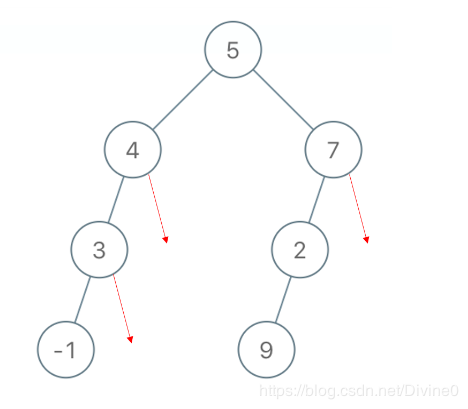
其中红色箭头对所有的None进行了标记。
现给出一个二叉树以这种形式序列化的结果,请复原该二叉树并给出它的中序遍历。
输入格式:
一行合法的Python表达式,可解析为包含整数与None的列表
输出格式:
二叉树中序遍历的整数序列,以空格分隔
输入样例:
[5, 4, 7, 3, None, 2, None, -1, None, 9]
输出样例:
-1 3 4 5 9 2 7
输入样例2:
[5,1,4,None,None,3,6]
输出样例2:
1 5 3 4 6
注:树结构如图(红色箭头对None的对应位置进行了标记):
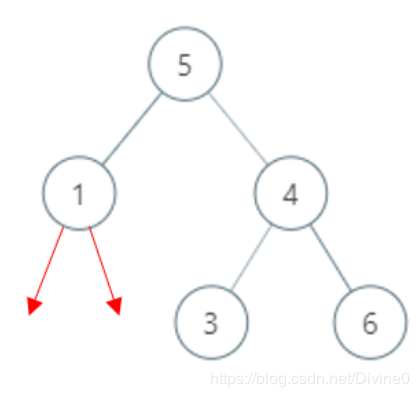
用嵌套列表形式表示列表反序列化后的树,每次创建新的子树时,将该子树添加到队列中,等当前子树绘制完毕后,从队列中取出下一个子树继续绘制
程序代码:def seq2tree(seq):
def BinTree(r):
return [r, [], []]
finalTree = BinTree(seq[0])
queue = [finalTree]
for num in seq[1:]:
currentTree = queue.pop(0)
if num == None:
if currentTree[1] == []:
currentTree[1].append(num)
queue.insert(0, currentTree)
else:
currentTree[2].append(num)
else:
if currentTree[1] == []:
currentTree[1] = BinTree(num)
queue.insert(0, currentTree)
queue.append(currentTree[1])
else:
currentTree[2] = BinTree(num)
queue.append(currentTree[2])
return finalTree
def inorderTree(tree):
if tree == [] or tree == [None]:
return []
else:
left = inorderTree(tree[1])
root = tree[0]
right = inorderTree(tree[2])
return left + [root] + right
lst = eval(input())
tree = seq2tree(lst)
inorder = inorderTree(tree)
print(*inorder)
2 翻转二叉树(10分)
题目内容:
给定一个二叉树,请给出它的镜面翻转。
为方便起见,本题只给出完全二叉树的层次遍历,请给出相应的翻转二叉树的中序遍历。
备注:
这个问题来自开源软件开发者Max Howell在Google面试被拒的经历 :
谷歌:我们90%的工程师使用您编写的软件(Homebrew),但是您却无法在面试时在白板上写出翻转二叉树这道题,这太糟糕了
输入格式:
一行空格分隔的整数序列,表示一个完全二叉树的层次遍历
输出格式:
一行空格分隔的整数序列,表示翻转后的二叉树的中序遍历
输入样例:
4 2 7 1 3 6 9
输出样例:
9 7 6 4 3 2 1
解题思路:因为题目中说明了给定的序列为一个完全二叉树的层次遍历,所以无需考虑存在None节点的情况,翻转后的二叉树的中序遍历,即为对原二叉树先递归访问右子树,再访问根节点,最后递归访问左子树
程序代码:def inorder(root):
if root * 2 + 1 <= len(lst) - 1:
inorder(root * 2 + 1)
result.append(lst[root])
if root * 2 <= len(lst) - 1:
inorder(root * 2)
lst = list(input().split())
lst = ['0'] + lst
result = []
inorder(1)
print(*result)
3 多叉树遍历(10分)
题目内容:
给定以嵌套列表形式给出的多叉树,求它的后序遍历
注:每个代表非空多叉树的列表包含至少一项;列表第一项代表节点值,其后每一项分别为子树;遍历子树时以列表下标从小到大的顺序进行。
输入格式:
一行合法的Python表达式,可解析为嵌套列表形式的多叉树结构
输出格式:
一行整数,以空格分隔
输入样例:
[1,[2,[3,[4],[5]],[6]],[7],[8,[9],[10]]]
输出样例:
4 5 3 6 2 7 9 10 8 1
解题思路:先递归后序访问多叉树的所有子树,再访问根节点
程序代码:def postorderTree(tree):
if len(tree) == 1:
return tree
else:
result = []
for i in range(1, len(tree)):
result += postorderTree(tree[i])
result += [tree[0]]
return result
lst = eval(input())
postorder = postorderTree(lst)
print(*postorder)
作者:Divine01