【C语言-数据结构与算法】-树与二叉树概念哈夫曼树的构造

树&二叉树&哈夫曼树Ⅰ 树A. 树的概念B. 树的表达形式（存储结构）C. 树的遍历a. 广度优先遍历（队列）b. 深度优先遍历（堆栈）Ⅱ. 二叉树A. 二叉树的有关概念B. 二叉树中相关公式C. 二叉树的存储结构Ⅲ 哈夫曼树及编码A. 构造哈夫曼树a. 频度统计b. 生成哈夫曼树B. 哈夫曼编码C. 解码 Ⅰ 树

由于树的应用场合很少，不是很实用，所以在此只做简单介绍。

A. 树的概念

树状图是一种数据结构，它是由n（n>=1）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
每个结点有零个或多个子结点；没有父结点的结点称为根结点；每一个非根结点有且只有一个父结点；除了根结点外，每个子结点可以分为多个不相交的子树

树的存储结构：非线性结构，一对多

关于树，有几个相关的词需要了解：节点， 叶子节点， 节点的度，树的度，我简单介绍一下有关树的这几个词。

节点的度：一个节点的子节点数量，称为该节点的度。
叶子节点：度为0的节点。
节点(非叶子节点)：度不为0的节点。
树的度：树中节点的度的最大值。

以以下这个树为例，我们来搞清楚关于树的这几个名词。

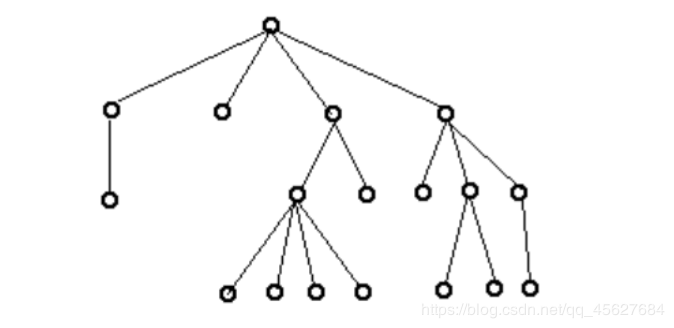
树的度：4
树的层数(高度，深度)：4
树中的节点总数：18
叶子节点数：11

B. 树的表达形式（存储结构）

由于树的每一个节点的最大子节点数量是不确定的，意味着其子节点数量不确定，因此，很难给出一个相对稳定的存储结构。

typedef struct TREE_NODE { USER_TYPE data; int childCount; struct TREE_NODE **children; }TREE_NODE;

USER_TYPE 根据用户需要存入的数据类型改变。

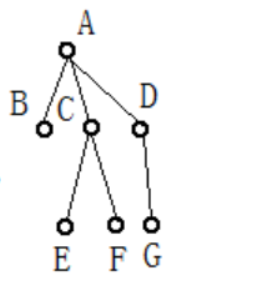
也可以用连续存储空间表示一棵树，如上面这颗可以表示为

哈夫曼树 数据 二叉树 C语言 算法 数据结构